Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Электромагнитные поля и волны.-2

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

1.87 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 117 8 9 10 11 > Следующая >>>

при x=0: а) H yII = H yIII и б) EzII = EzIII ; при x=d: в) H yI = H yII

Удовлетворяем граничным условиям, получим равенства:

из а) C + D = M ; из условия б) - C + D = -i								α3 M ;
								α2
из в) B = Ce- iχd + Deiχd ; из г) iα B = -α Ce- iχd + α												2	Deiχd .
				1	2							2
Определим C, D из первых двух равенств
	1		α	3		1				α	3
D =	1	M 1 - i		3	; C =	1	M 1		+ i		3
D =		M 1 - i			; C =		M 1		+ i
2			α2		2					α
2			α2		2					α	2

и г) EzI = EzII .

(6.25)

Введем обозначения в третье и четвертое равенства

Ce- iχd = C1 ; Deiχd = D1 , тогда B = C1 + D1 и iα`1B = -α2C1 +α 2D1 , откуда

		1			α
D1	=			+ i	1	,

		2	B 1		α2
		2			α2

		1			α	1
C1	=			- i		1

		2	B 1		α2		.
		2			α2

Переходим к прежним обозначениям:

	− iχ d		1				α			iχd		1		α
								1
Ce		=		B	1	− i			; De		=		B 1 + i	1	.
							α
			2									2		α2
								2

В (6.25), (6.26) делим одно выражение на другое и приравниваем

- i

+ i

2iχd

α2

- i

α2

+ i

α2

Преобразуем в (6.27) комплексные выражения

α3

iϕ1

ϕ1 = arctg

α3

+ i

= 1 + i

где

e2iχd =

α2

α1

α3

α1

iϕ

- i

ϕ2 = arctg

= 1 + i

где

α2

iϕ

e2iχd =

= e2i(ϕ1 + ϕ2 ) .

- iϕ

(6.26)

(6.27)

(6.28)

(6.28а)

	Из равенства				комплексных
	функций в (6.28а)следует фа-
	зовое соотношение
	χd = ϕ1 + ϕ2 + πm						(6.29)
	Подставляем ϕ1,ϕ2 из (6.28) в
	(6.29), получим
	χd = arctg	α1		+ arctg		α3		+ πm (6.30)

	α		2		α		2

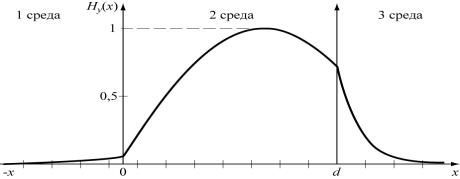
Рис.6.2. Векторный треугольник по-	В соотношение (6.30) подста-
стоянных распространения	вим введенные обозначения из

(6.24), получим

ωε

;

и окончательно

ωε 1

χ n

ωε 3

χ n

χd = arctg

+ arctg χ

+ πm .

(6.31)

Выражение (6.31) есть дисперсионное уравнение планарного диэлектри-

ческого волновода для волны типа Em = Em0, где m-число вариаций (переходов через ноль) косинуса или синуса вдоль поперечной оси x.

6.3. Дисперсионные уравнения

Дисперсионные уравнения (6.17) и (6.31) преобразуем к виду, удобному для расчетов, графического построения и последующего анализа.

Воспользуемся векторным треугольником коэффициентов распростране-

ния (рис.6.2) в волноводном слое и выражениями в виде

β = n2 k0 sinθ ; χ = n2 k0 cosθ

(6.32)

гдеβ - коэффициент фазы волны, распространяющейся вдоль оси z,

χ - поперечное волновое число стоячей волны, k2 -волновое число волны, рас-

пространяющихся в среде с показателем преломления n2 . С учетом k0 = 2λπ (λ - 61

заданная длина волны) , а также соотношений (6.11а)÷(6.11 в), из (6.32) получим

систему для поперечных постоянных величин во всех средах:

γ =

2π

χ =

2π

n cosθ ,

n2 sin 2

θ − n2

− n2 sin 2 θ

2π

ξ =

β =

n2 sin 2

θ − n2

k 2 − χ 2

Подставим значения γ , χ,ξ из (6.33) в (6.17), получим функцию:

n2 sin2

θ − n2

n2 sin2

θ − n2

F(θ) =

arctg

+ arctg

+ πm

n2 cosθ

2πn2 cosθ

(6.33)

(6.34)

Введем величину Nm =n2 sinθ , называемую эффективным показателем

преломления [38]. Тогда (6.33) и (6.34) можно записать в виде

γ =

2π

χ =

2π

ξ =

2π

Nm2 − n12

n22 − Nm2

Nm2 − n32

− n2

G(θ )Hm

arctg

+ arctg

+ πm

2π

− N m

− Nm

(6.35)

(6.36)

После подстановок типа (6.35) в уравнение (6.31) оно принимает вид:

N 2

− n2

N 2

− n2

F(θ)

arctg

+ arctg

2π

− N 2

n12

n2 − N 2

n32

n2 − N 2


	+ πm	(6.37)

6.4. Анализ дисперсионного уравнения и выводы

1.Дисперсионное уравнение (6.36) или (6.37) позволяет получить условия существования в планарном волноводе, распространяющейся моды. Так при за-

данных параметрах среды n1,n2,n3 и длины волны λ существование моды с ин-

дексом m возможно при определенной величине эффективного показателя преломления Nm = n2 sinθ , т.е. при определенном угле падения θ волны на гра-

ницу раздела. Чтобы корни, входящие в функцию arc tg дисперсионного урав-

нения (6.36) или (6.37) были вещественными числами и волна распространялась бы только в слое, должно выполняться неравенство

N 2 - n2		³ 0 или n2 sin 2 θ - n2 ³ 0 , или углы θ			³ arc sin	n1,3	.	(6.38)
				1,2
m	1,3	2	1,3			n2

При различных значениях величин показателей преломления сред n 1,2,3 из
(6.38) следует рассчитать угол θкр			= θmax ³ max[θ1 ,θ2 ], который называется уг-
лом отсечки.	При углах θ < θ max (меньших критического) работать нельзя, т.к.

начинается распространение волны в покровном или в базовом слоях, а не толь-

ко в планарном слое волновода. Например, отсечка волноводной моды наблюда-

ется при Nm= n3, если n1<n3<n2.

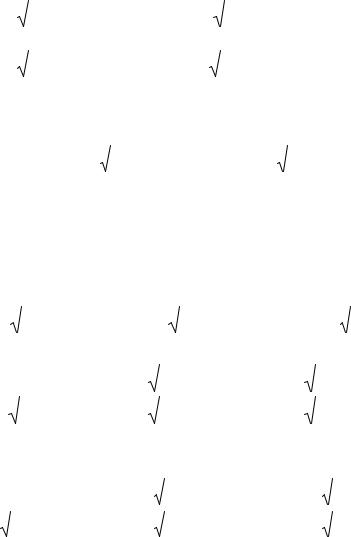
2. Необходимо построить семейство дисперсионных кривых G(θ )Hm ,

F (θ )Em (6.36) или (6.37) при изменении угла θ в пределах θmax £θ £ π / 2 , соот-

ветствующих разным модам, т.е. значениям m , при заданных параметрах n1,n2,n3,. На рисунке 6.3, к примеру, представлены такие дисперсионные зави-

симости для разных Hm-мод трехслойного планарного волновода. Т.к. величина

Рис. 6.3. Дисперсионные характеристики для волн типов H0,H1,H2

N m = n2 sinθ изменяется в ограниченных пределах n1 < N m < n2 , то при за-

данной толщине волновода d число существующих мод также конечное.

3. Если n1 ¹ n3 и n3 > n1 , то для каждой моды на заданной длине волны λ суще-

ствует (рис 6.3) критическая толщина волноводного слоя d	( H m )	,	(Em )	, соот-
ствует (рис 6.3) критическая толщина волноводного слоя d	крm	,	dкрm	, соот-
63

ветствующая отсечке волноводной моды (N m = n3 ) (при которой прекращается распространение волны), определяемая из соотношений:

πm + arctg

2 − n2 )

2π

(n22 − n32 )

( Hm )

крm

(6.39)

n22 − n32

(n 2

− n

2 )

πm + arctg

− n32 )

2π

(Em )

(n22

d крm

(6.40)

n22 − n32

4. Если m=0, то из (6.39) и (6.40) получается минимальная толщина вол-

новода для моды H0 и E0. Очевидно, в случае симметричного волновод (n1 = n3 )

минимальная толщина волновода будет равна нулю.

5. При заданной длине волны из рис.6.3 следует, что имеется интервал для

толщины волноводного слоя, при котором наблюдается режим одна мода

dкр.ближайшего > d > dкр. рабочего		(6.41)
типа	типа волны

Обратное, для заданной толщины волновода существует интервал длин волн, соответствующий работе на одной моде. При увеличении толщины d и

λ− const , растет число распространяющихся в планарном волноводе мод.

6.Фазовое соотношение (6.29) и (6.18) позволяют определить набег фаз

на толщине волновода - χd , состоящий из суммы фазовых сдвигов при отра-

жении волны от первого и третьего слоев и фазы πm , определяемой модой.

В курсовой работе следует рассчитать для заданных параметрах сред n1,n2,n3, длине волны λ и моде с индексом m дисперсионную характеристику,

размер волноводного слоя, полосу рабочих частот, угол отсечки и критические углы, фазовые набеги и параметры γ , χ,ξ в диапазоне частот.

6.5. Определение мощности, распространяющейся внутри слоев

Средняя за период мощность, проходящая по волноводу через единицу его ширины (по оси y), определяется формулой:

	1	∞ R		R
	1		&	&
P =		[E × H			* ]	dx	(6.42)
P =		[E × H			* ]	dx	(6.42)
	2	−∞∫			z
	2	−∞∫

Для волн типа Hm, после раскрытия векторного произведения с учетом имеющихся компонент в планарном волноводе, средняя за период мощность,

передаваемая вдоль оси z, равна:

∞ & & *

1 ∞

P = −

Ey H x dx =

dx .

(6.43)

2 −∞∫

2W −∞∫

E y

где W – волновое сопротивление среды , равное W =

= -

(6.44)

H y

H x

Чтобы найти выражение передаваемой мощности моды Hm , в системе

(6.17) выразим все коэффициенты через любой один, например С, который бу-

дет являться амплитудным коэффициентом и определяться мощностью волны,

распространяющейся в волноводе.

	ξ				ξ
B = C cos χd +		sin χd	,	D =		C , M	= C	(6.45)
B = C cos χd +	χ	sin χd	,	D =	iχ	C , M	= C	(6.45)
	χ				iχ

С учетом (6.45), выражения для полей (6.14),(6.15) и (6.16) принимают вид:

& I

−γ

( x−d )

−iβz

cos χd +

−γ ( x−d )

−iβz )

H x

= −

ωμ 0

C cos χd +

sin χd e

& I

= C

(6.46)

E y

sin χd

;

& I

cos χd +

sin χd

−γ ( x−d )

−iβz

iωμ

= −

−iβz

H x

ωμ 0

C cos χd

sin χd e

& II

−iβz

(6.47)

= C cos χd +

sin χd e

;

= −

cos χd +

sin

χd

−iβz

H z

iωμ0

& III

ξχ

−iβz

& III

ξχ

−iβz

& III

ξχ

−iβz

Ey = Ce

;

H x

= −

;

H z

= −

(6.48)

iωμ

ωμ

Найдем выражения мощностей (6.43) в различных слоях

Первая и вторая среды

C 2

2 ∞

C 2

2 ∞

P I =

cos χd

sin χd

∫ e−2γ ( x−d ) dx =

cos χd +

sin χd

∫ e

C 2

μ0

cos

χd +

χ sin χd

, где

4W I γ

C 2

W II

P II =

∫

cos(χx)

sin(χx)

dx =

ε 0 n2

C 2

∫

cos2

(χx) + 2

sin(χx)cos(χx) +

sin 2

(χx) dx

−2γx dx ,

(6.49)

(6.50)

	μ0		C	2	0	2
Третья среда W III =		; P III =			∫ e 2ξx dx =	C		(6.51)
	2		2W	III		III	ξ
	ε 0 n3				− ∞	4W

Величины мощностей при найденных значениях постоянных распростра-

нения в поперечном направлении (γ , χ ,ξ ) и значении угла ввода (6.38), могут быть рассчитаны.

Если задана величина вводимой мощности (по заданию), то можно опре-

делить коэффициент С. Для этого сумму мощностей в трёх слоях следует поло-

жить равной заданной мощности Р.

P I + P II + P III = P

(6.52)

После нахождения мощности, передаваемой в волноводном слое, следует определить параметр коэффициент локализации рабочей моды Гр в виде

Г р	=	P II	×100% , оценивая при этом качество волновода. Величину коэффициента
		P

локализации рабочей Гр можно оптимизировать, поскольку она изменяется от толщины слоя d, угла θ , параметров среды n1,n2,n3.

6.6. Фазовая скорость волн в слоях

Фазовая скорость волны в волноводном слое это параметр, который опре-

деляется величиной β

следующим образом: υ

, из (6.32)

β = n

ω sinθ ,

поэтому

υф

(6.55)

n2 sinθ

Сравнивая (6.55) со скоростью распространения волны в диэлектрике с

параметрами ε		μ		, получим	c		< υ		, откуда следует, что волна в слое по от-

	2		0		ε			ф
	2		0					ф
						2

ношению к скорости света в неограниченном диэлектрике является быстрой.

Фазовая скорость поверхностных волн в 1-й и 3-й средах также может быть определена с учетом (6.12а) и (6.12в)

; υф3 =

k 2 n2

ф1

+ γ

n3 1 +

ξ 2

n3 1 +

0 3

ω 2 μ

n 2

Преобразуем, например υф3 , представив корень в виде

1 +

ξ 2

= 1 + K33 , где

ω 2 μ0ε 0 n32

γ 2

K З3

= 1 +

ξ 2

− 1, K З1

= 1 +

− 1 коэффициент замедления для

μ0ε

0 n3

0 n1

3-го

слоя

для первого.

Тогда

фазовая

скорость волны в 3-ей среде

υф3

. в первой υф1

n3 (1 + K з3 )

n1 (1

+ K з1 )

Коэффициент замедления характеризует уменьшение фазовой скорости в покровных диэлектрических слоях по сравнению со скоростью света в этих ди-

электриках. В курсовой работе следует построить зависимости постоянных распространения, фазовых скоростей и коэффициентов замедления от частоты для всех слоев и сделать выводы.

6.7.Картина распределения полей в слоях

Картина распределения составляющих векторов E и H в слоях для за-

данного типа волны строится в поперечном направлении (вдоль оси x, при y,z-

постоянных) представляет интерес, т.к. наглядно позволяет проверить выпол-

нение граничных условий, характерное влияние значения индекса “m” на изме-

нение полей в волноводном слое и изменение по экспоненте полей в слоях (ско-

рость затухания), прилежащих к волноводному слою.

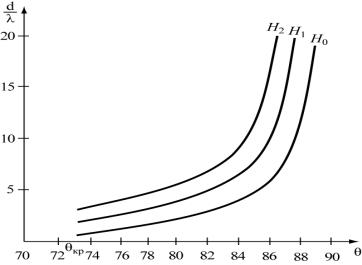
На рис 6.4 (в качестве примера) представлена зависимость изменения компоненты Ну(х) для моды Е1. Построение картины распределения полей вы-

полняется с помощью выражений (6.46), (6.47), (6.48). Для этого следует под-

ставить в уравнения все найденные коэффициенты (γ,χ,ξ,C), фазу волны поло-

жить равной постоянному значению (например, ϕ = ωt − βz = 0 ). Далее, изменяя координату х в пределах геометрии соответствующих слоев, получают зависи-

мость каждой компоненты электромагнитного поля.

Рис. 6.4. Изменение составляющей магнитного поля H y (x) в трехслой-

ном волноводе с параметрами n1<n3<n2 на волне типа Е1 .

Если по заданию необходимо определить поляризационную характери-

стику (см. раздел 2)или найти уравнение силовой линии для вектора, то делать это следует для вектора с 2-мя компонентами.

6.8. Структура электромагнитного поля в волноводном слое

Распределение векторов E и H в пространстве волновода (по координа-

там х, z) на заданном типе волны при фиксированном времени называют струк-

турой электромагнитного поля. Структура поля строится либо по эпюрам, либо по уравнениям векторной линии. Во втором случае следует записать мгновен-

ные выражения составляющих вектора для слоя, в котором будет сроиться структура поля, с учетом найденной амплитуды и коэффициентов. Уравнение

векторной линии имеет вид	dx	=	dy	=	dz	,	(6.56)

	ax a y az

где ax , a y , az - компоненты вектора, поле которого желательно построить.

Например, для моды H1 во второй среде, для вектора H . Из (6.47) находим

H x

H zII

= −		β		C	cos(χx) +	ξ sin(χx) cos(ωt − βz)
= −				C	cos(χx) +	ξ sin(χx) cos(ωt − βz)
		ωμ				χ
		ωμ	0			χ	.	(6.57)
		χ		ξ cos(χx) − sin(χx) sin(ωt − βz)			.	(6.57)
=		χ	C
=			C
	ωμ 0
	ωμ 0			χ

Видно, что векторная линия H лежит в плоскости xoz, имея две компоненты.

В соотношение (6.53) подставляется Hx и Hz (6.54), проводится разделение функций по переменным интегрирования (x, z) (для четных функций ( cos(χx)) и

для нечетных ( sin(χx)) отдельно составляются выражения), интегрируются ра-

венства. Получают две функциональные зависимости координаты z от коорди-

наты x и константы интегрирования (например, аN) для четных и не четных слу-

чаев. Затем, задается величина постоянной аN → а1, и изменением координаты

0<x<d, получают координаты z. Построив эту зависимость, отмечаем на ней ве-

личину а1-const, видим, что она замкнутая кривая. Задавая другое значение кон-

			R
станте - а2 , получаем следующую линию вектора H . Вектор E (6.47) представ-
лен одной компонентой вида E II (x, z) = C	cos (χx ) +	ξ	sin (χx ) cos (ωt − β z ), и
лен одной компонентой вида E II (x, z) = C	cos (χx ) +		sin (χx ) cos (ωt − β z ), и
y		χ
		χ

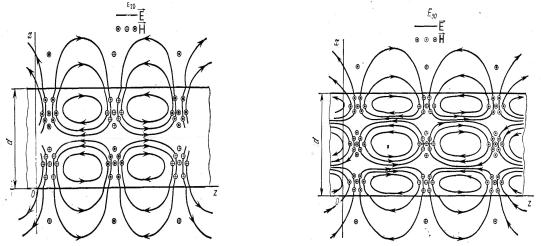
отображается в структуре густотой силовых линий в координатах x и z. На рис. 6.5, в качестве примера, приведены структуры полей моды Е20 и моды Е30

Рис.6.5. Структура электромагнитного поля моды Е20 и моды Е30 для симметричного планарного волновода.

<<< < Предыдущая 1 2 3 4 5 67 / 117 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.2023214.14 Кб3Электромагнитная экология.-1.pdf
#
05.02.2023135.98 Кб0Электромагнитная экология.-2.pdf
#
05.02.2023118.93 Кб0Электромагнитная экология.-3.pdf
#
05.02.2023196.13 Кб1Электромагнитная экология..pdf
#
05.02.2023652.23 Кб9Электромагнитные поля и волны.-1.pdf
#
05.02.20231.87 Mб6Электромагнитные поля и волны.-2.pdf
#
05.02.20232.38 Mб29Электромагнитные поля и волны.-3.pdf
#
05.02.20234.03 Mб7Электромагнитные поля и волны.-4.pdf
#
05.02.20233.52 Mб24Электромагнитные поля и волны.-5.pdf
#
05.02.20234.03 Mб30Электромагнитные поля и волны.-6.pdf
#
05.02.20234.17 Mб33Электромагнитные поля и волны..pdf