Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Электромагнитные поля и волны.-2

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

1.87 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 116 7 8 9 10 11 > Следующая >>>

А из второго уравнения системы (5.21) находим коэффициент затухания

	q 1	∂V	E=E0		ω 2 D		(5.23)

k ′′ = −n0 ε V (E0 ) ∂E				− V (E)2 V (E)
						∂

Так как коэффициент фазы k ′ < 0 , то волна распространяется против оси
OX. Поскольку постоянное поле E0		направленно по оси OX (от плюса к мину-

су), анодный электрод располагается у нас вначале координат, при х=0, то k ′ < 0

означает, что волны зарождаются на катоде и бегут к аноду.

В обычных условиях, т.е. при E < Eпор , коэффициент затухания k ′′ < 0 , т.к ∂V / ∂E = μn > 0 , а это означает, что волна затухает в направлении своего рас-


пространения. Однако, если E > Eпор , величина					∂V / ∂E < 0 и тогда слагаемое в
(5.23) ( − n		q	1	∂V ) становится положительным и будет больше ω 2		D	. В резуль-
(5.23) ( − n				∂V ) становится положительным и будет больше ω 2			. В резуль-
	0	ε V ∂E			V 2	V

тате чего k′′ изменит свой знак. Это означает, что волна будет усиливаться в на-

правлении своего распространения.

Коэффициент усиления на единицу длины будет

= −n

q 1 ∂V

−

ω 2

∂

(5.24)

ε V ∂E

V 2

ус

а усиление волны на длине кристалла L составит

K = e K усL

(5.25)

Для заданной частоты ω студент в своей работе должен рассчитать и по-

строить зависимость K ус = f (E) , которая будет имеет вид как на рисунке 5.5; оп-

ределить E при котором K ус = max . Определить длину L диода Ганна и усиление

в режиме слабого сигнала из условия	(k ′)L = ωL /V = 2π . Возможная область
усиления находится при E1 < E0 < E2 .	Максимум усиления достигается	при
E = Emax . В этой точке и следует найти L и K (5.25) и напряжение U =E max		, ко-
торое необходимое подать на диод Ганна.

Второй случай, когда полагаем заданной величину k и будем находить частоту ω . Случай, когда задано k (вещественное), а отыскиваетсяω , рассмат-

ривается аналогично. В этом случае комплексными будут частоты ω& = ω′ − iω′′ . 50

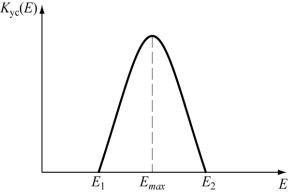
Рис. 5.5. График зависимости коэффи-

циента усиления от напряженности

электрического поля в диоде Ганна.

Из (5.18) и (5.19) получим

ω′ = −kV (E) ,			(5.26)
ω ′′ = k 2 D∂ + n0	q ∂V
		∂E .	(5.27)
	ε
То что ω′ = −V (E)			характеризу-
k

ет отрицательную скорость означает,

что волна бежит против оси OX, т.е.

от катода к аноду. Из (5.27) видно, что

ω′′ > 0	будет всегда, когда ∂V / ∂E > 0 .
В	этом	случае	волна


e j (ωt − kx )				= e −ω ′′t e(ω ′t − kx )	затухает	во	времени.	Когда	же
n		q	∂V + k 2 D < 0 и ω′′ < 0 сигнал будет усиливаться при kL = 2π . Необходимо
n
	0	ε ∂E		∂

построив зависимость ω′′ = f (E) и найти область усиления сигнала.

Выводы

1.Дисперсионное уравнение для анализа режимов усиления и генерации

вдиоде Ганна позволяет определить коэффициент фазы и коэффициент затуха-

ния волны при различных концентрациях носителей в образцах на частоте ω .


		2.		При заданной частоте ω и E > Eпор , величина ∂V / ∂E < 0 , и тогда
k ′′ < 0 , т.е. волна усиливается в направлении распространения.
		3.		При заданной величине постоянной распространения к при условии
n		q	∂V + k 2 D < 0 и ω′′ < 0 сигнал будет усиливаться при kL = 2π .
n
	0	ε ∂E		∂

4. Конкретные числовые данные должны быть приведены в выводах по-

сле построения и анализа всех графиков, получаемых в работе.

6. Плоский диэлектрический (планарный) волновод Тема курсовой работы: Разработка планарного волновода для интегральной

оптики. [10, 14, 15, 16, 17, 26, 27, 28, 29, 38].

Технические данные: Рабочая длина волны задана (например, 0,5 мкм);

Параметры слоев задаются (например, n1=1.64; n2=1.72; n3=n1);

Тип волны в планарном волноводе задается (например, Н10);

Мощность на входе волновода задается (например, 0,5 мВт).

В работе необходимо: Решить уравнения Максвелла; получить выражения для электромагнитных полей; получить дисперсионное уравнение для расчета геометрии волноводного слоя, определения диапазона длин волн, в пределах ко-

торого распространяется только указанный тип волны; определить мощности,

распространяющиеся внутри слоев. Изобразить картины электромагнитных по-

лей в слоях.

6.1. Волны магнитного типа Hm (TEm)

Оптические волноводы (световоды) – это направляющие диэлектрические структуры, по которым может распространяться электромагнитная энергия в видимой или инфракрасной областях спектра. Явление распространения элек-

тромагнитных волн по оптическим волноводам может быть рассмотрено строго с позиций волновой теории, т.е. уравнений Максвелла и соответствующих гра-

ничных условий.

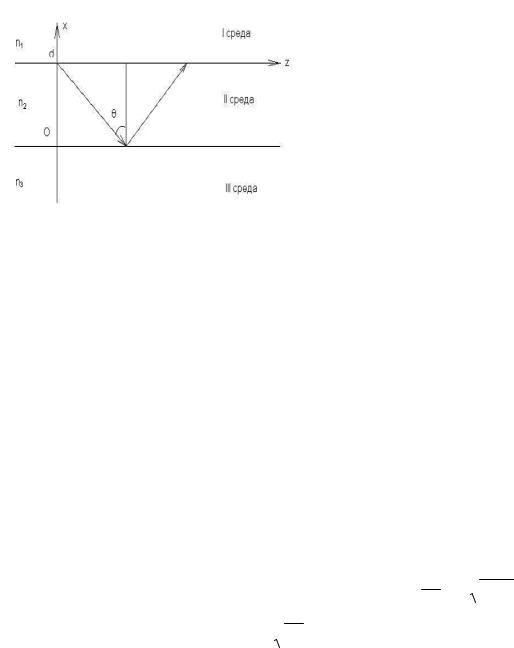
Планарный диэлектрический волновод представляет трехслойную струк-

туру (рис.6.1) с размерами, не ограниченными в двух направлениях y и z. Сред-

ний (второй) слой толщиной d имеет самый высокий показатель преломления,

т.е.: n2 > n1 и n2 > n3 , причем, n1 < n3 < n2 . На границах второго слоя с первым и третьим выполняются условия полного внутреннего отражения.

Среды планарного волновода изотропные, не имеют потерь, магнитная проницаемость их одинакова и равна проницаемости воздуха . Световая вол-

на распространяется во втором слое вдоль оси z, отражаясь полностью от гра-

ниц раздела (рис.6.1). В таком диэлектрическом волноводе возможны волны ти-

па H (Hz≠0, Ez=0) и типа E (Ez≠0, Hz=0), а также гибридные - ЕН. 52

Рассмотрим волну типа Н. Направим вектор E вдоль неограниченной ко-

ординаты у ,	∂	= 0 , тогда вектор H будет лежать в плоскости, ортогональной у,
	∂ y

т.е. иметь две составляющие Hx, Hz.

Задача: решить уравнения Максвелла для системы из трех диэлектриче-

ских сред, удовлетворить его граничным условиям и получить дисперсионное уравнение, необходимое для определения постоянной распространения во вто-

рой среде. Определить размеры второй среды, позволяющие распространять волну заданного типа.

Рис.6.1 – Планарный волновод в сечении

y=const

	R	R		R			R
x0		y0		z0		x0
	∂			∂	R		∂
		0			= iωεE ;
		0			= iωεE ;
	∂x			∂z			∂x
H x		0	H z			0

Уравнения Максвелла в отсутствии сторонних токов и потерь в среде имеют вид:

R R R R

rotH = +iωεE ; rotE = −iωμH . (6.1)

Для определения выраже-

ний составляющих электромаг-

нитного поля из уравнения (6.1)

запишем его в виде определите-

лей с учетом имеющихся ком-

понент векторов:

R	R
y0	z0
	∂	R
0		= −iωμ H	(6.2)
0	∂z	= −iωμ H	(6.2)
E y	∂z
E y	0

Раскроем (6.2) и получим равенства для составляющих векторов в виде

	∂E	y		∂E	y		∂H x		∂H z	= iωεE y
H x =			; H z = −			;		−			(6.3)

	iωμ∂z			iωμ∂x			∂z		∂x

После подстановки Hx и Hz в (6.3) в третье соотношение и введения обо-

значений волнового числа свободного пространства k0 = 2λπ = ω ε0μ0 ; n – пока-

зателя преломления среды, равного n = ε r , получим

∂ 2E	y	+	∂ 2E	y	+ k	2n2 E		= 0	(6.4)
							y
∂x2			∂z 2			0

Для бегущей волны вдоль оси z (2.13) решение может быть записано в виде:

		E		y	(z) = E		ym	e− iβz ,	(6.5)
				y			ym
где β – постоянная распространения волны в продольном направлении,									Eym -
амплитуда волны. Уравнение (6.4) после подстановки (6.5) запишется
	∂ 2E	ym	+ (n2k 2				− β 2 )Eym = 0 .		(6.6)
			+ (n2k 2				− β 2 )Eym = 0 .		(6.6)
	∂x2				0
	∂x2
В (6.6) обозначим δ значение постоянной в поперечном направлении
				δ 2 = (n2 k02 − β 2 ) ,					(6.7)
получим			∂ 2 E ym			+ δ 2 E ym = 0 .			(6.8)
получим						+ δ 2 E ym = 0 .			(6.8)
				∂x 2

Уравнение (6.8) определяет поведение электрического поля Ey в попереч-

ном направлении x. В случае кусочно-однородной диэлектрической структуры

(рис.6.1) уравнение (6.8) справедливо отдельно в каждой из трех однородных

сред, но при выполнении следующих условий:

а) амплитуды полей на бесконечности должны быть равны нулю, т.е.

E y (x) |x → −∞ = 0 и E y (x) |x → ∞ = 0 .

(6.9)

б) отсутствие потока энергии в поперечном направлении в первой и третьей средах, что эквивалентно резкому уменьшению полей вне второй сре-

ды. Для выполнения этого условия поле в 1 и 3 средах в уравнении (6.7) у по-

стоянной δ необходим знак минус, т.е.

δ 2 = β 2 − n2k	2	, при β > nk	0	.	(6.10a)
	0		0

в) во второй среде поле в поперечном направлении должно изменяться по гармоническому закону. Для этого необходимо, чтобы уравнение (6.9) имело комплексно-сопряженные корни , т.е.

δ 2 = n2k	2	− β 2 , где β < nk	0	.	(6.10б)
	0		0
		54

Используя решение (6.8) с учетом условий (6.9), (6.10а) и (6.10б), получим

выражения электромагнитных полей в каждом слое.

Первая среда: (x ≥ d) – покровный слой, поверхностная волна


δ	1	= γ = β 2	− n2 k 2		> 0		(6.11a)
	1		1	0
			d 2E I
Уравнение (6.8) должно иметь вид				y		− γ 2E I	= 0 .
Уравнение (6.8) должно иметь вид						− γ 2E I	= 0 .
			dx2			y
			dx2

Составляя характеристическое уравнение ( p1,2 = ±γ ), получаем решение

I	=		γ (x − d )	+ Be	− γ (x − d )	− iβz	.	(6.12а)
E y	=	Ae		+ Be	e		.	(6.12а)

Учитывая условие (6.9), коэффициент А в (6.12а) необходимо приравнять нулю. Подставим значение поля Е Iу в систему (6.4), получим выражения полей моды Н в первой среде в комплексном виде:

& I

= −

− γ (x − d )

− iβz

& I

= Be

− γ (x − d )

− iβz

ωμ0

;

− γ (x − d )

− iβz

& I

H z

iωμ0

Вторая среда (0<x<d), β < n2k0 - волноводный слой, постоянная

δ 2 = χ = n22k02 − β 2 > 0 .

Уравнение (6.8) с учетом (6.11б) и его решение принимают вид:

(6.13а)

(6.11б)

	∂ 2 E II
	y	+ χ 2 E II = 0 , (характеристическое уравнение p = ±iχ ),
		+ χ 2 E II = 0 , (характеристическое уравнение p = ±iχ ),
	∂x2	y		1,2
	∂x2
E II = Ceiχx + De− iχx ei(ωt − βz)				или E II = [C cos(χx) + iD sin(χx)]ei(ωt − βz)
y						y
Подставив (6.13) в (6.3) получим

		E II = [C cos(χx) + iD sin(χx)]ei(ωt − βz)
		y
			β		[C cos(χx) + iD sin(χx)]ei(ωt − βz)
		H xII = −	β
		H xII = −	ωμ
			ωμ	0
			χ			[− C sin(χx) + iD cos(χx)]ei(ωt − βz)
		H zII = −	χ
		H zII = −
			iωμ0

(6.14)

(6.13б)

Третья среда: (x ≤ 0) , β > n3k0 - базовый слой.

	δ		3	= ξ =		β 2 - n		2k	2	> 0	(6.12в)
			3					3	0
III		=			ξx	+ Ne	- ξx		i(ωt - βz)
E y		=		Me		+ Ne		e

Используя (6.3) и (6.9), полагая N=0, получим:


		= Meξxei(ωt - βz)
E III		= Meξxei(ωt - βz)
	y		β			ξx	i(ωt - βz)
	III	= -	β			ξx	i(ωt - βz)	(6.13в)
H x					Me e
H x					Me e
		ωμ0
			ξ			Meξxei(ωt - βz)
H III		= -	ξ
H III		= -
	z	iωμ		0
				0

Для определения констант B,C,D,M воспользуемся граничными условия-

ми для тангенциальных компонент векторов на границе диэлектрических сред

E1τ = E2τ , H1τ = H 2τ :
1)		E yI		= E yII при x=d и любом значении z получаем соотношение
					B = C cos(χd ) + iD sin(χd )					(6.15а)
2)		H I		= H II	при x = d и любом значении z получаем соотношение
			z	z
		γ		Be- γ (d - d )ei(ωt - βz) = -		χ		[- C sin(χd ) + iD cos(χd )]ei(ωt - βz)	или
	iωμ		0	Be- γ (d - d )ei(ωt - βz) = -		iωμ	0	[- C sin(χd ) + iD cos(χd )]ei(ωt - βz)	или
	iωμ					iωμ

					γB = χ[C sin(χd ) + iD cos(χd )]					(6.15б)
3)		E yII		= E yIII	при x=0 и любом значении z имеем
		[C cos(χ × 0) + iD sin(χ × 0)]ei(ωt - βz) = Meξ × 0ei(ωt - βz) , откуда C = M								(6.15в)

4) H zII = H zIII при x = 0 и и любом значении z :

iχD = ξM

(6.15г)

Четыре однородных линейных уравнения (6.15а) – (6.15 г) объединим в систему относительно B,C,D,M.:

B = C cos(χd ) + iD sin(χd )

C = M

(6.16)

γB = χ[C sin(χd ) + iD cos(χd )]

iχD = ξM

Нетривиальное решение (6.16) существует, когда определитель равен нулю.

1 - cos(χd )

- i sin(χd )

- sin(χd )

i cos(χd )

= 0

- ξ

iχ

В данном определителе столбцы соответствуют множителям B,C и D со-

ответственно. Раскрывая определитель, получим соотношение:

- χ sin(χd ) + ξ cos(χd ) + γ cos(χd ) +

γξ sin(χd ) = 0

+ ξ

. tgχd =

откуда

- χtg(χd ) + ξ + γ + γξ tg(χd ) = 0

1 - γξ

χ 2

χd = arctg

+ π × m , m = 0,1,2,…

(6.17)

γξ

1 -

здесь m – индекс типа волны в волноводном слое для координаты х. Рассматри-

ваемые моды (типы волн) обозначаются Hm.

Уравнение (6.17) является дисперсионным уравнением волн типа Нm, рас-

пространяющихся в диэлектрическом волноводе, которое связывает параметры

ε , μ0	трех сред и геометрию второго слоя d с рабочей частотой							f . Уравнение
(6.17)	может быть [41] преобразовано к виду:
	arctg	x + y	= arctgx + arctgy при условии xy<1.
	arctg		= arctgx + arctgy при условии xy<1.
	1 - xy
	Условие удовлетворяется, т.к. γξ < χ 2 , что следует из (6.12а) ÷ (6.12в). То-
гда запишем (6.17) в виде:
	χd = arctg			γ	+ arctg	ξ	+ π × m ; m = 0,1,2,...	(6.18а)
	χd = arctg			χ	+ arctg		+ π × m ; m = 0,1,2,...	(6.18а)
				χ		χ

Примечание : Если среды 1 и 3 (рис.6.1)будут иметь одинаковый показа-

тель преломления (n1=n3) - случай симметричного волновода, тогда γ = ξ , а

уравнение (6.18а) приводится к виду

					2γ
				χd = arctg(				) + πm .			(6.18б)
				χd = arctg(	χ 2 − γ 2			) + πm .			(6.18б)
	В случае, когда один из слоев будет металлическим, величину поперечной
постоянной в нем, γ				или ξ , следует считать равной нулю, а дисперсионное
уравнение (6.18), например, в случае ξ = 0 , принимает вид:
				χd = arctg		γ	+ πm				(6.18в)
				χd = arctg			+ πm				(6.18в)
						χ
	6.2. Волны электрического типа Еm или ТМm
	В случае поперечно-магнитной волны Hz=0, при условии								∂	= 0 ,	отлич-
	В случае поперечно-магнитной волны Hz=0, при условии									= 0 ,	отлич-
									¶y
ными	от	нуля,	будут	компоненты электромагнитного поля Ez,					Нy ,		Ex, т.е.
R	R	R	R	R
H = H y y0 ,		E = Ex x0 + Ez z0 . Получение выражений для составляющих полей и

дисперсионного уравнения можно сделать, применяя принцип перестановочной двойственности к уравнениям и выражениям предыдущего параграфа, но мож-

но повторить получение этих выражений. Из (6.3) и (6.6)

¶H y

¶E

z -

¶E

Ex = -

, Ez

, H y

(6.19)

iωε

¶z

iωε

¶x

iωε

¶x

¶z

¶2H y

2n2 - β 2 )H

= 0

(6.20)

¶x2

Для каждой из сред вводя свои поперечные постоянные δi ,и учитывая

требование конечности полей при x → ±∞ , получаем из (6.20) решения.

Первая среда (рис.6.1) характеризуется: ¥> x ³d,

β > n1k0 .

Обозначим δ

= γ =

β 2 - n2k

> 0 , тогда уравнение (6.20) принимает вид

γ (x - d )

- γ (x - d )

i(ωt - βz)

H y

- γ

H y = 0 , а его решение H y

= Ae

+ Be

¶x

Чтобы при x → ∞ величина вектора оставалась конечной, следует А = 0. 58

Поле в первой среде с учетом соотношений (6.19) будет иметь вид:

		= Be− γ (x − d )ei(ωt − βz)
H I		= Be− γ (x − d )ei(ωt − βz)
	y		β
						Be− γ (x − d )ei(ωt − βz)
E I		=							(6.21)
E I		=	ωε						(6.21)
	x		ωε		1
					γ			Be− γ (x − d )ei(ωt − βz)
E I		= −			γ
E I		= −		iωε
	z			iωε			1

Вторая среда - волноведущий слой: 0 < x < d , β < n k

,δ

= χ =

n2 k 2 − β 2

> 0 , со-

ставляющие поля волны типа Е для этого слоя

[Ce

− i χ x

i χ x

i ( ω t − β z )

;

= [Ce

−iχx

+ De

iχx

i(ωt−βz)

;

E x

H y

ωε 2

[− Ce

− iχ x

iχ x

i (ω t − β z )

(6.22)

E z

ωε

Третья среда: x<0 , β > n k

= ξ =

β 2 − n2k

> 0 . Поле имеет вид:

III

ξx

i(ωt − βz )

H y

ξx

i(ωt − βz )

III

(6.23)

E x

ωε

Me ξx ei(ωt − βz )

E III

iωε

Для упрощения записи выражений полей вводим обозначения:

α1 =	γ	; α 2 =	χ		; α 3 =	ξ		(6.24)
	ωε 1		ωε	2		ωε	3

Выделим из (6.21)÷(6.23) составляющие, входящие в граничные условия:

= iα1Be

− γ (x − d )

= Be

− γ ( x − d )

H y

E II

= −α

Ce− iχx + α

Deiχx

− iβz

;

= Ce− iχx + α

Deiχx

− iβz

Meξx

= Meξx

E III

= −iα

H III

Запишем граничные условия:

<<< < Предыдущая 1 2 3 4 56 / 116 7 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.2023214.14 Кб3Электромагнитная экология.-1.pdf
#
05.02.2023135.98 Кб0Электромагнитная экология.-2.pdf
#
05.02.2023118.93 Кб0Электромагнитная экология.-3.pdf
#
05.02.2023196.13 Кб3Электромагнитная экология..pdf
#
05.02.2023652.23 Кб17Электромагнитные поля и волны.-1.pdf
#
05.02.20231.87 Mб13Электромагнитные поля и волны.-2.pdf
#
05.02.20232.38 Mб45Электромагнитные поля и волны.-3.pdf
#
05.02.20234.03 Mб18Электромагнитные поля и волны.-4.pdf
#
05.02.20233.52 Mб37Электромагнитные поля и волны.-5.pdf
#
05.02.20234.03 Mб41Электромагнитные поля и волны.-6.pdf
#
05.02.20234.17 Mб50Электромагнитные поля и волны..pdf