Электромагнитные поля и волны.-2

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

= (Ee2τ × n) / m

Сравнивая (5.4) с (5.1), получаем σ = (Ee2τ × n) / m =

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

1.87 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 115 6 7 8 9 10 11 > Следующая >>>

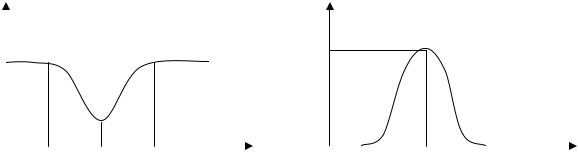
k2 d 2

= π − π λ . Подставляя эти выражения в (4.19), получим

2 2 λ0

cos ϕ = −

1 n1

cos π

+ (1 −

[(1

)

λ0

)

]

4 n2

= −

{[1 +

](1 + cos π

) −

− cos π

)} =

(

)

λ0

1 n1

(4.31)

= −

{[1 +

(

)

](cos π

)

− 2

(sin

)

}

2λ0

= −

(

) + [

(

)

+ 1](sin π

)

2λ0

Полагая вновь ϕ = π + iβ = ϕ ′ + iϕ ′′ , получим

e2β - 2{

(

) -[

(

) +1] × (sinπ

)2 × eβ +1 = 0

(4.32)

2 n1

2λ0

С помощью (4.32) находятся зависимости от длины волны для e β (λ )

и β (λ)

(рис.4.4)

e− β

max

λmin

λ0

λmax

λmin

λ0

λmax

б)

Рис. 4.4. Графики ослабления и прохождения поля от рабочей длины

волны

Зависимость постоянной распространения волны от частоты β (ω)

назы-

вается дисперсионной характеристикой структуры. Если структура работает в полосе непропускания, то значение β (ω) позволяет определить полосу частот фильтра по заданному уровню пропускания. Поэтому следует построить графи-

ки ослабления поля e− β (λ ) и β (λ) как функции длины волны или частоты и най-

ти границы полосы запирания фильтра для созданной структуры.

с). На границе полосы пропускания β = 0 , eβ = 1 и из (4.32) получим со-

отношение для определения полосы пропускания многослойной структуры в

(

) − 1

виде

(sin π

)

(4.33)

2λ0

(

)

+ 1

Откуда полоса пропускания

λ = ±η .Например, для MgF2 – ZnS ( табл.4.1):

λ0

(sin π

)

1,33 − 1

0,133

0,062

., что дает

= ±0,16 .

2λ0

1,33 + 1

2,133

λ0

Итак, полоса пропускания этой многослойной структуры составляет ≈30%.

В действительности полоса пропускания зеркала будет меньшей. Если

число слоев N , то величина пропускания фильтра составит e Nβ . Если мы до-

пускаем увеличения величины пропускания в два раза по сравнению с тем, что

мы имеем при λ = λ0 , то следует учитывать, что это возможно при

e− Nβ (λгр ) = 2e− Nβ (λ0 ) . Отсюда получаем уравнение для расчета граничной длины

		β (λгр )		β (λ	)	-	1	×Ln2
волны λгр	e		= e						,	(4.34)
				0		×e N

Решение этого уравнения следует получать из графика e β (λ ) .

Выводы

1. Дисперсионное уравнение для многослойной диэлектрической структуры

(4.19) может быть построено при различных параметрах сред и размерах слоев.

2. Периодическая структура из чередующихся слоев с высоким и низким пока-

зателями преломления способна обеспечивать высокие затухания поля в полосе пропускания. При 8÷10 периодах структуры ослабление не менее 50÷60 раз.

3.По частотным передаточным характеристикам структуры можно определять ширину полосы непропускания. По уровню 3 дБ от минимума коэффициента передачи полоса структуры уменьшается при увеличении числа N.

4.После построения и анализа всех графиков, получаемых в работе, можно привести конкретные числовые данные.

5. Плоские волны при анализе усиления и генерации в диоде Ганна

Тема курсовой работы: Анализ усиления и генерации волн в диоде

Ганна с помощью теории плоских волн. [7, 20, 42, 44, 45, 46, 47].

Технические данные: Исходный полупроводниковый материал - задается;

концентрация доноров n=1015÷10 20 ; длина образца, площадь сечения;

напряжения на диоде 1÷10 В; ток в максимуме 340 ÷370 мА;

желаемая частота генерации 8÷11 ГГц.

Вопросы, подлежащие рассмотрению: Принцип устройства и работы дио-

да Ганна; построение зависимостей ВАХ, скорости от напряженности и от тем-

пературы, подвижности от концентрации и температуры (ход всех характери-

стик необходимо пояснить). Плоские волны в образце, их параметры и диспер-

сионное уравнение. Получение условий усиления и генерации в заданном час-

тотном диапазоне.

Введение

Диод Ганна представляет собой полупроводниковый (п/п) кристалл с омическими контактами на противоположных гранях. В отличие от других п/п

приборов диод Ганна не имеет p-n переходов. Название диода связанно с явле-

нием открытым в 1963 г. Ганном в подобных структурах. Оказалось, что при подаче на диод напряжения от источника постоянного напряжения в диоде воз-

никают периодические колебания тока с частотой , лежащей в диапазоне СВЧ.

Эта генерация СВЧ колебаний имеет критический характер и возможна лишь при напряжении на диоде больше некоторого порогового значения U пор . Период колебаний оказывается прямо пропорционален длине кристалла. Причина воз-

никновения СВЧ колебаний связана с особенностями нелинейной зависимости тока в диоде от напряжения на нем. Эта зависимость описывается уравнением

	I = α × (1 - k )e(1−α )	+ k (1 - e−α	+ αe1−2α ) ,	(5.1)
где α = U U 0	; k = I s I0 - коэффициент качества диода (к=0,4÷0,5 диод считает-
ся хорошиv;	k=0,8÷0,9 – среднего	качества);	Is – ток	насыщения; I0-

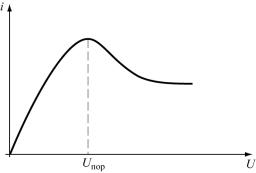
максимальная величина тока; U0 = Uпор – напряжение на диоде при макси-

мальной величине тока; U - текущая величина напряжения. Зависимость (5.1)

рассчитывается при заданных параметрах тока и напряжения и имеет вид

(рис.5.1). Главным является участок при U > U пор . На этом участке ток с ростом напряжения падает. Определив для переменного тока динамические проводи-

мость или сопротивление σ	∂	=	∂i	,	R	=	∂U , можно заметить, что при посто-

			∂u		∂		∂i

янном напряжении U > Uпор величины R,σ < 0 . Если активное сопротивление

Рис. 5.1.Вольт амперная характери-

стика диода Ганна.

среды R < 0	или σ	∂	< 0 , то P = i2 R < 0 , значит колебания нарастают, т.е.
∂		∂	∂

«электронная» мощность P выделяется активной средой.

Физическая причина падающего участка тока на вольтамперной характе-

ристике связанна с особенностями зависимости энергии электрона от его им-

пульса в зоне проводимости материала п/п. Связь кинетической энергии с им-

пульсом имеет вид EK	=	mV 2	=	p 2	, где р- импульс, m – масса электрона, V- ско-
пульсом имеет вид EK	=		=	2m	, где р- импульс, m – масса электрона, V- ско-
	2			2m
рость его. Полная энергия E = E0 +						p 2	, где E0 потенциальная энергия на дне зо-
рость его. Полная энергия E = E0 +						2m	, где E0 потенциальная энергия на дне зо-
						2m

ны проводимости и зависимость E от р показана на рис.5.2. Как видно, здесь существует один энергетический минимум, вблизи дна которого и находятся в основном все электроны зоны проводимости. Кривизна этой энергетической

E( p)

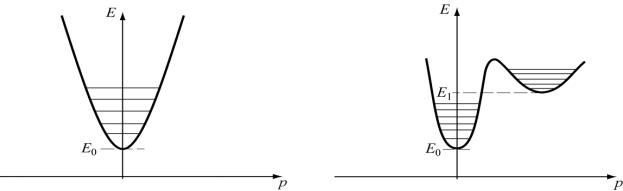
ямы определяется массой m носителя заряда. Чем выше кривизна, тем меньше

масса m. В ряде п/п зависимость при больших р имеет другой вид (рис.5.3)

Рис. 5.2. Зависимость E-энергии от	Рис. 5.3. Зависимость E-энергии от р-
р- импульса	импульса в двух долинном материале

. Как видно, здесь имеется два энергетических минимума E0 и E1 . В отсутствии внешнего электрического поля все электроны находятся в первом из них с энер-

гией E0 . В этом минимуме зависимость E( p) имеет большую кривизну и, сле-

довательно, носители обладают малой массой и высокой подвижностью, что означает также высокую проводимость. Действительно, плотность тока прово-

димости можно записать в двух формах

jпр = σE или jпр = enV ,

(5.2)

где σ - проводимость материала полупроводника, n -число электронов в объеме.

Для скорости V и импульса mV справедливо уравнение движения Ньютона

	∂	R	R
		(mV ) = eE −		mV			,		(5.3)
	∂t
					τ
где τ- время релаксации импульса; величина						mV		-	характеризует уменьшение
						τ

импульса за счет релаксации, т.е столкновений электрона с решеткой и передачи ей импульса и энергии. В твердых телах τ мало по сравнению с периодом коле-

баний. Инерционным членом	∂(mV )		можно пренебречь, и из (5.3)	получим
	∂t
		V = eτE / m		(5.3a)
			44

где μ = eτ / m - подвижность носителей - является характеристикой материала.

В сильном электрическом поле, когда скорость электронов V оказывается большой, велик и импульс- p = mV = eτE и основная часть электронов оказыва-

ется в энергетическом минимуме с энергией E1 . В этой области эффективная масса m, как видно из рис. 5.3, велика (в GaAs примерно в 40 раз больше) и со-

ответственно подвижность электронов и проводимость σ падают по мере за-

полнения электронами дна зоны вблизи E = E1 . Резкое падение σ с ростом E

приводит к падению тока как функции напряжения (рис.5.1).

5.1. Основные уравнения электромагнитного поля для диода Ганна

Основные уравнения теории электромагнитного поля могут быть приме-

нены к анализу работы диода Ганна. Поэтому анализ ЭМП и В в диоде Ганна начнем с уравнений Максвелла, которые преобразуем для последующей работы

	R		= ρ .
rotH = jполн , rotE = - ¶B ,		divB = 0 , divD	= ρ .
	¶t
Так как размеры диода малы, то поле в диоде можно рассматривать как
квазистатическое, членом ¶B / ¶t	и вообще магнитным полем можно пренеб-
речь. Взяв div от первого уравнения, получаем ноль, остальные имеют вид:
rotE = 0,	divD = ρ,	divjполн = 0 .	(5.6)

ния

ток

В выражении полного тока учитываем все три составляющие: ток смеще-

R	=	∂D = ε				R		R
j	=	∂D = ε	∂E , ток проводимости j					= enV (E) и «сторонний» диффузионный
см		∂t	∂t				пр
см							пр
jдиф = −eDдgrad (n) , где Dд -коэффициент диффузии. Ток получим в виде
			R		= ε		R		(5.7)
			j		= ε	∂E + enV (E) − eD grad (n)			(5.7)
				полн		∂t		д
				полн				д

Запишем выражение для объемной плотности заряда ρ . В состояние рав-

новесия заряд электронов полностью компенсирован зарядом решетки, поэтому

ρ = 0 . При движении электронов их распределение в пространстве образца мо-

жет стать неравномерным и этот заряд может оказаться не скомпенсированным.

Тогда можно записать для объемной плотности заряда

ρ = e(n − n0 ) ,

(5.8)

где n0, n – однородное и неоднородное распределение концентрации заряда в ре-

шетке. В результате получаем следующие три уравнения

∂

∂t

R		R		R
divεE + div(enV (E)) − ediv(D∂ grad (n))
R				R
divE =	e	(n − n ) , rotE = 0
divE =	ε	(n − n ) , rotE = 0
	ε		0
			0

(5.9)

(5.10)

Из конструкции диода следует, что электрическое поле E должно быть

направленно от положительно заряженного электрода к отрицательному и мо-

жет изменяться в этом же направлении. Примем это направление за ось OX, то-

обращается в тождество, так как

гда E = E(x)x0 . При этом уравнение rot(E) = 0

. Примем , что концентрация n-также изменяется только от оси

rot(E = E(x)x0 ) ≡ 0

х, тогда уравнения для E и n (5.9) и (5.10) с учетом (5.8) примут вид

∂n +

∂

−

∂

∂n ) = 0

(5.11)

(E)

∂x

∂t

∂x

д ∂x

∂E =

(n − n0 )

(5.12)

∂x

Из (5.3а) следует, что в силу того,

что заряд электрона e < 0 ,V и

E на-

правлены встречно; следовательно,

если

Ex = E > 0 , то Vx = −V < 0 Заменим по-

этому Vx

на − V

в формуле (5.11). Коэффициент диффузии носителей Dд

зави-

сит от подвижности носителей и температуры. В первом приближении он равен

Dд = (μn KбT ) /		e		= KбTτ / m	(5.13)

Kб -константа Больцмана, μn = eτ / m - подвижность электронов, таким образом

Dд также зависит от приложенного поля E. Окончательно основные уравнения для анализа работы диода Ганна принимают вид при q = e = −e

∂n −	∂	nV (E) + D		(E)	∂n	= 0	(5.14)
∂n −		nV (E) + D		(E)		= 0	(5.14)
∂t
∂t	∂x		д		∂x
			д
			46

∂E = -	q	(n - n0 ) ,	(5.15)
	ε
¶x

Параметры модели диода Ганна

Для решения уравнений (5.14)÷(5.15) необходимо знать зависимость V (E)

и D(E) . Эти зависимости находятся из экспериментальных данных.

V (E) приведена в [47] в виде

	μ		E + V		(		E		)4
	μ	n	E + V	нас	(				)4
V (E) =		n		нас		E		пор		,
								пор

				E			4
				E			4
			1 +
			1 +

				Eпор

где μ		=	n1 μ1	+ n2 μ2	- эффективная подвижность носителей.
	n
			n1	+ n2

Для GaAs

(5.16)

При E << Eпор скорость носителей равна V = μn E . При больших

E >> Eпор ,

V (E) ® Vнас . Величины μn и Vнас и Епор

являются параметрами математической

модели (5.16) для V (E) . Экспериментально установлено, что для GaAs

= 4000

= 4 ×105

, V

= 107

см

= 105

(5.17а)

пор

см

м нас

Подвижность электронов в слабом поле зависит от концентрации носителей и температуры. При T = 3000 K

μn

μi

(5.17б)

+ 10−17 n0

где μ = 8 ×103

см2

= 0,8

м2

;

n -концентрация

донорных примесей, для

GaAs.

В × с

обычно n0 = 2(1014

-1016 )

. Поэтому при любой температуре (T ¹ 3000 K )

см3

μn (T ) = μn (300 /T )1,14

(5.17в)

Величина Vнас

так же зависит от T

V = V

нас

(300)(300 /T )0,7

(5.17г)

нас

В задании на курсовую работу для разных приборов и материалов параметры

μi , n0 и T обычно задаются, зависимость V (E) строится , ее вид (рис.5.4) 47

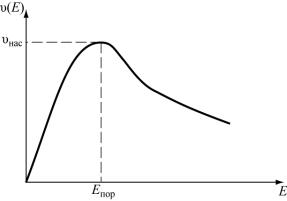
Работа прибора в генератор-

ном или усилительном ре-

жиме	возможна	в	режиме
E > Eпор (V < Vпор ).		Для		этого
следует вычислить для за-
данных n0 и T , Vпор и Епор
Коэффициент			диффу-
				Рис. 5.4. Зависимость скорости носителей от
зии в первом приближении,
когда	зависимостью			напряженности поля Е в образце диода.
				пара-
метров	от напряженности

поля E можно пренебречь, следует вычислять по формуле (5.13).

5.2. Дисперсионное уравнение для волн в диоде Ганна

Пусть помимо приложенного постоянного поля E0 в диоде Ганна распро-

страняется плоская волна, имеющая небольшую амплитуду. Определим ее ха-

рактеристики. Используем символический метод расчета и полагаем

E(x,t) = E0 + E1ei(ωt −kx) ,

где ω -частота колебаний плоской волны, k -волновое число, E1 -амплитуда вол-

ны, причем E1

<< E0 . Величину скорости движения носителей V (E)

разложим в

ряд по малой величине E1

V (E) = V (E

) +

∂V

E ei(ωt −kx) , D (E) ≈ D (E

) = D .

∂E

E = E0

∂

Поле E1 вызовет соответствующую модуляцию величины n - концентра-

ции носителей

n = n + n ei (ωt − kx)

Подставляем эти выражения в (5.14) и затем в (5.15)

iωn ei (ωt −kx )

−

∂

+ n ei (ωt

−kx) )(V (E

) +

∂V

E ei (ωt −kx ) ) + D

∂

+ n ei (ωt −kx) )

= 0 .

∂

∂x

∂E

E =E0

∂x

Отсюда, пренебрегая произведением n1 E1 и выпуская экспоненту, получим

iωn

+ikn V (E

) + ikn

∂V

E + k 2 D n = 0 или

∂E

E =E0

∂

∂V

[iω + ikV (E

) + k 2 D ]n + ikn

E = 0

(5.18)

∂

∂E

E =E0

− ikE

= −

(5.19)

Для того чтобы система однородных уравнений (5.18) и (5.19) имела ре-

шение, определитель ее должен быть равен нулю. Составим определитель

iω + ikV (E

) + k 2 D

ikn

∂V

∂

∂E

E =E0

= 0 .

− ik

Раскрывая этот определитель, получим дисперсионное уравнение, связы-

вающее круговую частоту ω и постоянную распространения k

ω = −kV (E

) + i(k 2 D

+ n

q ∂V

)

(5.20)

∂

0 ε ∂E

E =E0

5.3. Анализ дисперсионного уравнения

Проведем анализ дисперсионного уравнения для двух случаев.

В первом случае, считаем заданной частоту ω и будем определять зави-

симость k (ω) . Как видно из (5.20), параметр k

при этом будет комплексным. За-

′′ , где k′ - коэффициент фазы;

k′′ - коэффициент затухания.

пишем его k = k ′ −

в (5.20) и выделяем из него вещественную и мнимую части

Подставим k

{ω} = −k ′V (E0 ) + 2D∂ k ′k ′′,

q ∂V

0 = k ′′V (E

) + (k ′2

− k ′′2 )D

+ n

(5.21)

∂

ε ∂E

E=E0

Будем полагать, что коэффициент затухания волны k′′

не очень велик по

сравнению с коэффициентом фазы волны k ′, , т.е k ′′ << k ′ .

Тогда из первого уравнения (5.21)	находим коэффициент фазы
k ′ = −	ω
		(5.22)

	V (E0 )

<<< < Предыдущая 1 2 3 45 / 115 6 7 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.2023214.14 Кб3Электромагнитная экология.-1.pdf
#
05.02.2023135.98 Кб0Электромагнитная экология.-2.pdf
#
05.02.2023118.93 Кб0Электромагнитная экология.-3.pdf
#
05.02.2023196.13 Кб3Электромагнитная экология..pdf
#
05.02.2023652.23 Кб17Электромагнитные поля и волны.-1.pdf
#
05.02.20231.87 Mб13Электромагнитные поля и волны.-2.pdf
#
05.02.20232.38 Mб45Электромагнитные поля и волны.-3.pdf
#
05.02.20234.03 Mб18Электромагнитные поля и волны.-4.pdf
#
05.02.20233.52 Mб37Электромагнитные поля и волны.-5.pdf
#
05.02.20234.03 Mб41Электромагнитные поля и волны.-6.pdf
#
05.02.20234.17 Mб50Электромагнитные поля и волны..pdf