
Математика.-1
.pdf
x
Теорема 1. Функция (x) f (t)dt является первообразной от
a
функции f (x) .
Доказательство. Нужно доказать, что (x) f (x) .
Рассмотрим подробнее производную функции (x) . По определению,
(x) lim |
(x x) (x) . |
|
|
||
x 0 |
x |
|
|
|
|
|
|
|
x x |
x |
|
|
|
|
f (t)dt f (t)dt |
|
|
В данном случае, это |
lim |
a |
a |
, по свойству 2, интеграл |
|
|
x |
||||
|
|
x 0 |
|
|
|
по отрезку |
[a, x x] можно |
представить в виде суммы двух |
|||
интегралов, а именно, по [a, x] и [x, x x] . Чертѐж:
При этом интеграл по [a, x] там в разности есть ещѐ и со знаком «минус», то есть он в итоге сокращается.
|
x |
x x |
x |
|
x x |
|
f (t)dt |
f (t)dt f (t)dt |
|
f (t)dt |
|
lim |
a |
x |
a |
= lim |
x |
|
x |
|
x |
||
x 0 |
|
x 0 |
|||
По свойству 10, интеграл по отрезку [x, x x] как некоторое среднее значение, т.е. в какой-то умноженное на длину отрезка.
В общем случае длина была равна b a , а для
.
можно представить точке с [x, x x],
данного отрезка это
x x
|
|
f (t)dt |
|
x f (c) |
|
|
|
просто x . Тогда: |
lim |
x |
= lim |
= |
lim f (c) . |
||
x |
x |
||||||
|
x 0 |
x 0 |
|
x 0 |
31
Однако точка с [x, x x], |
поэтому при |
x 0 , |
точка c , |
которая |
|
находится где-то между x |
и |
x x , стремится |
к левой |
границе |
|
отрезка: c x . Поэтому в итоге |
lim f (c) |
= f (x) . |
|
|
|
|
|
x 0 |
|
|
|
Теорема 2. (Ньютона-Лейбница). Если F(x) - какая-либо |
|
||||
|
|
|
b |
|
|
первообразная от f (x) , то верна формула: |
f (x)dx F (b) F (a) . |
||||
|
|
|
a |
|
|
Доказательство. Если F(x) |
есть произвольная первообразная, то она |
||||
отличается на какую-то константу C от той первообразной, которую мы рассматривали в теореме 1. То есть F(x) (x) C , что означает
x |
|
|
|
|
|
|
|
|
|
F (x) f (t)dt C . |
Запишем это равенство в точке a , получится |
||||||||
a |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
F (a) f (t)dt C |
но |
ведь |
интеграл |
по |
одной |
точке |
это |
0, там |
|
a |
|
|
|
|
|
|
|
|
|
нулевая длина основания, |
а |
значит |
и |
нулевая |
площадь. |
Тогда |
|||
F(a) 0 C C . вот, |
кстати, |
мы заодно и установили, |
как связана |
||||||
константа C с выбором начальной точки a . |
|
|
|
|
|||||
(a) 0 , а на сколько по |
высоте отличается от любая другая |
||||||||
первообразная - это и есть значение C F(a) . |
|
|
|
||||||
|
|
|
x |
|
|
|
|
|
|
Итак, теперь ясно, что F (x) f (t)dt F (a) . |
|
|
|
||||||
|
|
|
a |
|
|
|
|
|
|
А теперь рассмотрим это выражение в точке b . |
|
|
|
||||||
b |
|
|
|
|
|
b |
|
|
|
F (b) f (t)dt F (a) , |
то |
есть F (b) F (a) f (t)dt . |
Но |
ведь |
|||||
a |
|
|
|
|
|
a |
|
|
|
переменная t вводилась исключительно для того, |
чтобы отличать x |
||||||||
внутри функции и на верхнем пределе интеграла. Теперь, когда перешли к фиксированным границам в интеграле, можно сделать
32

тривиальную замену x t и запись примет вид
b
f (x)dx F (b) F (a) , что и требовалось доказать.
a
Примеры
Пример.
Решение.
Пример.
1 |
x 2 |
|
|
1 |
|
|
|||||
|
|
|
|||
Решение. xdx |
|
|
= |
||
2 |
|||||
0 |
|
|
0 |
||
|
|
Пример. Найти интегралы
1 |
x3 |
|
|
1 |
|
|
|||||
|
|
|
|||
Решение. x 2 dx |
|
|
= |
||
3 |
|||||
0 |
|
|
0 |
||
|
|
|
|
02 |
|
|
1 |
. |
|||||
|
|
|
|||||||||
2 |
2 |
|
|
|
2 |
|
|
||||
1 |
|
|
|
|
|
|
|
2 |
|||
|
x2 dx |
|
и |
|
|
x2 dx . |
|||||
0 |
|
|
|
|
|
|
|
1 |
|||
13 |
|
03 |
|
|
1 |
. |
|||||
|
|
|
|
|
|||||||
3 |
3 |
|
|
|
3 |
|
|||||
2 |
x3 |
|
2 |
|
23 |
|
13 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
x 2 dx |
|
|
= |
|
|
. |
|
|||||||
|
3 |
|
|
|
|
|
|
|||||||
1 |
|
|
1 |
3 |
3 |
|
3 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
Пример. Найти интеграл |
sin xdx . |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
Решение. |
sin xdx = cos x |
|
= (cos cos0) = ( 1 1) 2 . |
|||||||||||
|
|
|
|
|||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Пример. Найти интеграл cos xdx .
0
33

|
|
0 |
|
Решение. cos xdx = sin x |
|
= 0 0 0 . |
|
|
|||
|
|
||
0 |
|
|
|
Вид формулы интегрирования по частям для определѐнного
b |
b |
||
интеграла: u(x)v (x)dx u(x)v(x) |
|
ba |
v(x)u (x)dx . |
|
|||
|
|||
a |
a |
||
Особенности замены переменной в определѐнном интеграле (пересчѐт пределов интегрирования, и можно не возвращаться к старой переменной, то есть не делать обратную замену).
4 |
1 |
|
|
x |
|
|
Пример. Вычислить интеграл |
|
dx |
||||
|
|
|
|
|||
|
|
|||||
0 |
|
|
x |
|||
Решение. При замене t 
 x мы адаптируем границы к новой переменной, то есть, если x [0,4] , то t [
x мы адаптируем границы к новой переменной, то есть, если x [0,4] , то t [
 0,
0, 
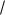 4 ] = [0,2] .
4 ] = [0,2] .
2 |
1 |
t |
|
2 |
|
|
2 |
|
|
Тогда |
2tdt |
= (2 2t)dt |
= (2t t 2 ) |
|
= 8. |
||||
|
t |
||||||||
0 |
|
|
0 |
|
|
0 |
|
||
|
|
|
|
||||||
|
|
|
|
|
|
|
Конечно, старые границы могут остаться прежними, например, при такой замене [0,1] отобразится в [0,1] . Но, как правило, при замене верхний и нижний предел интегрирования тоже изменяются.
Замена в определѐнном интеграле должна задаваться взаимнооднозначной функцией t (x) , то есть монотонной функцией. Иначе
можно столкнуться с такими парадоксами: |
например, t sin x , |
интеграл от 0 до . Тогда по переменной t |
получаем интеграл по |
промежутку [0,0] , и он был бы в любом случае равен 0. Чтобы
избежать такого противоречия, надо было |
бы |
разбить исходный |
|||||
интеграл по переменной x |
на 2 части, по |
|
|
|
и |
|
|
0, |
|
|
|
, . |
|||
|
|
|
2 |
|
|
2 |
|
34
Приложения определѐнных интегралов.
Пункт 1. Вычисление площадей фигур.
Так как площадь криволинейной трапеции связана с интегралом, то это приложение очевидно. Но есть особенности, связанные со строением геометрической фигуры, в некоторых случаях надо разбить фигуру на несколько частей.
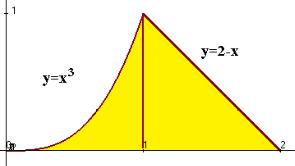
Пример. Найти площадь фигуры, ограниченной линиями
y 0, y x3 , y 2 x .
Решение. Построим чертѐж:
Так как верхняя граница после точки 1 переходит с одной кривой на другую, то придѐтся разбить на сумму двух вычислений по каждой
1 |
|
2 |
x4 |
|
1 |
|
|
x2 |
|
|
2 |
|
|
|
|
||||||||
|
|
|
|||||||||
|
|
|
|
|
|
||||||
|
3 |
|
|
|
|
|
|||||
части отдельно: x dx + (2 x)dx . Итак, получим |
|
|
|
|
2x |
|
|
|
|
||
|
|
|
|
|
|
||||||
4 |
|
|
|
2 |
|
|
|
||||
0 |
|
1 |
|
0 |
|
|
|
|
1 |
||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
1 |
|
1 |
|
3 |
|
1 |
|
1 |
|
3 |
|
|
= |
|
4 2 2 |
|
|
|
= |
|
2 |
|
= |
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||||||||
|
4 |
|
|
2 |
|
4 |
|
2 |
|
4 |
|
2 |
|
4 |
|
|
Пункт 2. Вычисление объѐмов тел вращения.
Если график функции вращать вокруг оси 0x, то получится так называемое тело вращения. Каждое сечение плоскостью,
паерпендикулярной оси 0x , это круг, его площадь равна f 2 (x) , так как f (x) это как раз и есть радиус (равно удалению вращающейся
b
точки от оси вращения). В итоге, V f 2 (x)dx .
a
35
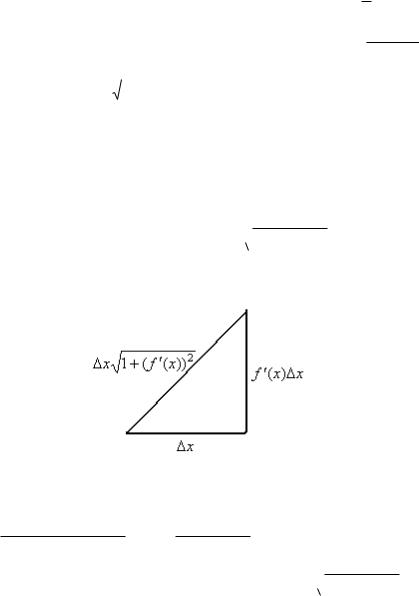
Пример. Вывести этим методом формулу объѐма шара V 34 R3 .
Решение. Чтобы получить шар, достаточно вращать верхнюю полуокружность, которая задаѐтся такой функцией: f (x) 
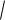 R2 x2 .
R2 x2 .
R |
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
R |
||
V f 2 (x)dx = |
|
R 2 x 2 |
2 dx = (R2 x2 )dx = |
|||||||||||||||
R |
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
R |
||
|
|
R |
|
x |
3 |
|
R |
|
|
|
R |
3 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||||
R2 x |
|
|
|
|
|
|
= |
2R3 2 |
|
|
= |
|
R3 . |
|||||
|
|
R |
3 |
|
|
|
3 |
|
|
3 |
|
|||||||
|
|
|
|
R |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пункт 3. Вычисление длины дуги кривой.
b
Формула для явно заданной кривой: L 
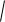 1 ( f (x))2 dx .
1 ( f (x))2 dx .
a
Доказательство. Разобьѐм область определения на n частей, рассмотрим подробнее одну часть графика.
Длина фрагмента кривой приближѐнно равна гипотенузе. При этом, тангенс угла наклона равен производной. Поэтому, если горизонтальный катет x то вертикальный равен f (x) x . Но в этом случае гипотенуза, по теореме Пифагора, равна:
li = 
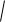 (x)2 ( f (x) x)2 = x
(x)2 ( f (x) x)2 = x
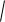 1 ( f (x))2 .
1 ( f (x))2 .
b
При переходе к пределу при n , получится L 
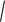 1 ( f (x))2 dx .
1 ( f (x))2 dx .
a
36

Чем круче наклон фрагмента графика, тем больше величина ( f (x)) 2 ,
и тем больше корень 
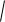 1 ( f (x))2 и соответственно, длина части этой кривой. Напротив, если график горизонтальный (функция = константа) то
1 ( f (x))2 и соответственно, длина части этой кривой. Напротив, если график горизонтальный (функция = константа) то 
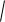 1 ( f (x))2 =
1 ( f (x))2 = 
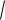 1 02 1. Длина такой кривой просто равна длине отрезка в области определения, то есть b a .
1 02 1. Длина такой кривой просто равна длине отрезка в области определения, то есть b a .
Для параметрически заданной в плоскости формула принимает такой
b
вид: L 
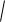 (x (t))2 ( y (t))2 dt .
(x (t))2 ( y (t))2 dt .
a
b
В трѐхмерном пространстве: L 
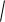 (x (t))2 ( y (t))2 (z (t))2 dt .
(x (t))2 ( y (t))2 (z (t))2 dt .
a
Длина кривой в полярной системе координат. Пусть кривая задана формулой r r( ) .
b
Тогда: L 
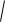 (r ( ))2 (r( ))2 d .
(r ( ))2 (r( ))2 d .
a
Доказательство этой формулы. Рассмотрим формулы взаимосвязи между полярными и декартовыми координатами:
x r cosy r sin
Теперь применим параметр таким же образом, как в прошлой
формуле был параметр t .
x() r() cos , y() r() sin .
Найдѐм производные:
x ( ) r ( ) cos r( ) sin y ( ) r ( ) sin r( ) cos
b
Их надо подставить в формулу: L 
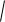 (x ())2 ( y ())2 d .
(x ())2 ( y ())2 d .
a
37

b
L 
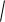 (r () cos r() sin )2 (r () sin r() cos)2 d
(r () cos r() sin )2 (r () sin r() cos)2 d
a
применим формулу сокращѐнного умножения в каждом квадрате под корнем. Там получатся квадраты и удвоенные произведения, которые, впрочем, сократятся, ведь они будут разного знака. Выражение под корнем преобразуется так:
(r ( ) cos r( ) sin )2 (r ( ) sin r( ) cos )2 = (r ( )) 2 cos2 (r( )) 2 sin 2 2r ( )r( ) sin cos + (r ( )) 2 sin 2 (r( )) 2 cos2 2r ( )r( ) sin cos = (r ( )) 2 (cos 2 sin 2 ) (r( )) 2 (cos 2 sin 2 ) =
(r ( )) 2 (r( )) 2 .
b
Поэтому и получается в итоге: L 
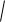 (r ( ))2 (r( ))2 d .
(r ( ))2 (r( ))2 d .
a
ЛЕКЦИЯ № 4. 07.03.2017
§5. Несобственный интеграл.
Если криволинейная трапеция бесконечно вытянута вправо или вверх, то может быть конечная площадь. Примеры:
1 |
dx |
|
|
|
1 = 1. |
||
Пример. |
|
= |
x |
||||
|
|
|
|||||
2 x |
|||||||
0 |
|
|
|
0 |
|||
|
|
|
|
||||
Но ведь область значений E(f) не является ограниченной. При вычислении мы даже и не заметили, что функция неограниченная в
окрестности точки 0, т.е. lim |
|
1 |
|
|
. Так как первообразная |
|
|
|
|
||
|
|
|
|
||
|
|
||||
x 0 2 |
|
x |
|||
ограниченная, и в неѐ можно просто подставить x 0 и x 1. Вот
1
график этой функции  : 2
: 2 x
x
38
1 |
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
dx |
|
|
|
|
|
||||
|
|
|
можно рассматривать как предел |
lim |
|
|
|
. |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
0 |
2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b 1 |
0 |
2 x |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
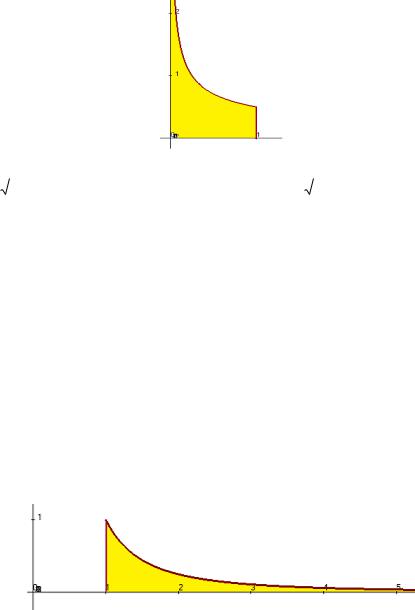
Пример. Вычислить |
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. Такой интеграл можно рассматривать как предел |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
b |
dx |
|
|
|
|
|
|
|
|
|
|
b |
dx |
|
|||
интегралов вида |
при b . Если вычислить |
то получится |
|||||||||||||||||||||||||||
2 |
|
2 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x |
|
|
|
|
|
|
|
1 |
x |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1 |
|
b |
|
|
1 |
|
1 |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
. Предел lim 1 |
|
|
1 |
0 1. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
x |
|
1 |
|
|
b |
|
1 |
|
|
b |
|
|
b |
|
b |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Несмотря на неграниченность трапеции под интегралом, площадь конечна. Здесь область определения D(f) не является ограниченной. Тем не менее, трапеция слишком узкая, т.е. еѐ ширина убывает достаточно быстро, чтобы площадь не превысила некоторое число. Так может быть, к примеру, если площади криволинейных трапеций между соседними целыми абсциссами убывают со скоростью сходящейся геометрической прогрессии.
39
Определение. Если |
функция f (x) определена и непрерывна на |
|
b |
[a, ) , то предел lim |
f (x)dx называется несобственным интегралом |
b a |
|
|
|
1-го рода от функции |
f (x) , и обозначается f (x)dx . |
a
Аналогично с помощью предела можно определить и несобственный интеграл 2 рода. Так, если функция имеет бесконечный предел на
правой границе b то надо отступить на некоторое расстояние |
и |
||||||
посчитать конечный интеграл, а затем перейти к пределу. |
|
||||||
Определение. Если функция |
f (x) определена и непрерывна на [a, b) |
||||||
|
|
|
|
|
|
b |
|
и при этом |
предел lim f (x) , |
то |
lim |
|
f (x)dx называется |
||
|
x b |
|
|
0 |
a |
|
|
|
|
|
|
|
|
|
|
несобственным |
интегралом |
2-го |
рода |
от |
функции f (x) , |
и |
|
b
обозначается f (x)dx .
a
Итак, если неограниченная D(f), то интеграл называется
несобственным интегралом 1-го рода, а если E(f) то несобственным
интегралом 2-го рода.
Если предел существует и является конечным числом, то несобственный интеграл называется сходящимся, если предел не существует или равен бесконечности, то интеграл называется
расходящимся.
Кстати, для сравнения, геометрическая прогрессия также бывает сходящейся либо расходящейся. Если площадь такой бесконечно вытянутой криволинейной трапеции разбить на части по целым числам, например от 1 до 2, от 2 до 3 и так далее, то если они образуют сходящуюся прогрессию, и в сумме равны некоторой константе, то интеграл сходится.
Примеры расходящихся несобственных интегралов.
40
