Математика.-1

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

f (x) f (x)dx

.pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

2 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 1814 15 16 17 18 > Следующая >>>

0,5								0,5							(x	3	)	3				(x	3	)	5
sin(x			3										3		(x		)					(x		)
				)dx =						(x				)												... dx		=
				)dx =						(x				)	3!							5!				... dx		=
0									0						3!							5!
0,5					x	9		x	15								x		4	1/ 2					x	10	1/ 2		x	16	1/ 2
0,5						9			15										4	1/ 2						10	1/ 2			16	1/ 2
		3
		3													=																... =
	x			3!				5!			... dx				=			4						10		3!		16 5!			... =
0				3!				5!										4		0				10		3!	0	16 5!			0
0																				0							0				0
	1						1								1						...очевидно, здесь 3 и последующие

24 4				210 10 6								216 16 120

слагаемые заведомо меньше 10 5 , и не повлияют на 4-й знак после запятой, поэтому приближѐнное значение

1		1	=	1			1		0,0156 0,000016 0,0156.
24 4		210 10 6		64		1024		60

Как видим, даже 2-е слагаемое можно было не рассматривать, т.к.

оно меньше, чем 10 4 .

4. Решение дифференциальных уравнений.

Можно представить неизвестную функцию y(x) в виде степенного ряда y a0 a1x a2 x2 ... и подставить его в дифференциальное

уравнение, тогда решение найдѐтся тоже в виде ряда, т.е. можно знать строение решения, его график и т.д. даже без аналитического выражения этой функции. .

Пример. y y решить с помощью степенных рядов. y a0 a1x a2 x2 ... тогда y a1 2a2 x 3a3 x2 ...

Из равенства a1 2a2 x 3a3 x2 ... = a0 a1x a2 x2 ... получаем: a1 a0 , 2a2 a1 , 3a3 a2 и так далее.

В этом случае все коэффициенты можно последовательно выразить

через a

. А именно, a

, a

и т.д.

Тогда y a

a x a

x2 ... = a

1 x

...

здесь видно,

что в скобках получилось разложение экспоненты. Итак, y a0ex .

131

Эту единственную константу можно переобозначить C и получится знакомый из вид общего решения такого уравнения: y Ce x .

Пример. Решить дифференциальное уравнение																																																						y y с помощью
степенных рядов.
y a							a x a										2		x2			...								y a									2a						2	x 3a x2 ...
				0					1								2																				1								2					3
y 2a											2		3 2a x 4 3a x2																								...
											2											3											4
Подставим в уравнение.
2a		2	3 2a x 4 3a																						4		x2			... = a											a x a								2	x2		... тогда:
		2							3																4												0						1						2
2a2 a0 ,																			3 2a3 a1 ,
4 3a4 a2 ,																			5 4a5 a3 ,
6 5a6 a4 ,																			7 6a7 a5 ,
...																			...
Из этих двух групп равенств можно все чѐтные коэффициенты
выразить через a0 , а все нечѐтные через a1 .
a						1		a			,			a													1			a
a								a			,			a										3 2						a
	2				2				0						3									3 2							1
a								1			a								1		a				,				a							1			a						1		a , ...
	4						4 3						2					4!					0								5				5		4				3				5!			1
аналогично,														a											1			a			,	a						1		a			,		a					1	a		, a				1	a ,...
																6									6!					0			5				7!				1						8		8!			0			9		9!		1
Тогда							y a							a x												a0				x2				a1		x3						a0			x4				a1		x5		... =
Тогда							y a					0		a x																x2						x3									x4						x5		... =
												0							1								2!								3!								4!						5!
																											2!								3!								4!						5!
										x			2					x		4																	x		3					x	5
y a					1					x								x				...								a			x				x							x			... =						a		cos x a sin x .
y a				0	1																	...								a			x														... =						a	0	cos x a sin x .
				0							2!								4!													1					3!						5!											0					1
											2!								4!																		3!						5!
Впрочем, константы можно переобозначить через C1 ,C2																																																								и записать
решение в привычном виде																																			y C1 cos x C2 sin x .

132

Ряды ЛОРАНА.

Ряд вида an (z z0 )n , то есть содержащий как положительные, так

и отрицательные целые степени, называется рядом Лорана. Совокупность слагаемых с нулевой и положительной степенью называется его правильной частью, а отрицательных - главной частью.

an (z z0 )n

правильная часть,

an (z z0 )n

главная часть, еѐ

n 0

a n

также можно переписать в виде:

z0 )n

n 1 (z

...

a 2

a 1

a0 a1 (z

z0 ) a2 (z z0 )

...

(z z0 )2

z z0

Теорема 1. Область сходимости ряда Лорана есть кольцо вида r z z0 R .

Доказательство. Распишем по отдельности на главную и

			a n
правильную часть: an (z z0 )	n	+		.
			(z z0 )n
n 0		n 1

1. Для правильной части верна теорема Абеля, ведь это обычный степенной ряд. Правильная часть абсолютно сходится в некотором

круге z z0 R .

	a n
2. Рассмотрим главную часть ряда Лорана		.
	(z z0 )n
n 1

Сделаем в ней замену с целью представить через положительные

1
степени и применить теорему Абеля. w		. тогда для новой
	z z0

переменной w ряд принимает такой вид: a n wn . Это степенной

n 1

133

ряд, его круг сходимости с центром в 0. То есть,

z z0

, обозначим

r , вот и получили

z z0

r .

Итак, область сходимости есть r		z z0		R , это кольцо.

Крайние случаи:

Если r 0 : круг с выколотой точкой 0 z z0 R .

Это происходит, если в главной части лишь конечное количество слагаемых. Их значение не существует только в самой точке z0 , а в

любой точке из еѐ окрестности - существует. Поэтому из области сходимости исключается лишь одна точка.

Если R : внешняя часть некоторого круга r

z z0

(z 1)n

Пример. Найти кольцо сх ряда Лорана

(z 1)

n 0

n 1

Решение. Найдѐм отдельно по радикальному признаку Коши область сходимости правильной и главной части.

				n					z 1
				n
1.	Для	(z 1)			получается									1, т.е.			z 1		5


								5
	n 0		5n
	n 0		5n
			1										1							1
2.	Для					получается										1, т.е.		z 1			.

			2n (z 1)n								2	z 1								2
	n 1		2n (z 1)n								2	z 1								2
Ответ. Кольцо сходимости:							1			z 1					5 .
							1

						2
						2

134

(z 2)( z 3)

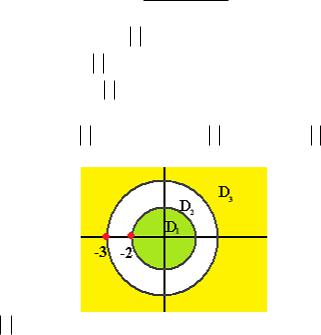
ЛЕКЦИЯ № 13. 16.05.2017

Разложение в ряд Лорана с помощью геометрической прогрессии.

Пример. Разложить функцию :

а) в ряд Лорана в кольце 2 z б) во внешней области z 3 в) в ряд Тейлора в круге z 2.

Во-первых, если центр кольца 0, а точки разрыва z 2 и z 3, то
есть 3 области: D1 z 2 ,	D2 2 z 3 ,	D3 z 3 .

Чертѐж:

D2 2 z 3 кольцо, расположенное между двумя точками

разрыва, так, чтобы ни одна из низ не была внутри кольца.

Разложим на простейшие дроби. Это действие необходимо в любом случае, независимо от того, в каком множестве надо получать разложение в ряд.

A(z 3) B(z 2)

(z 2)( z 3)

z 3

(z 2)( z 3)

( A B)z (3A 2B) 0z 1

A B 0

система:

3A 2B 1

A 1, B 1

f (z) =

z 2

z 3

135

1) Для разложения в ряд Лорана в кольце, надо вынести за скобку иногда константу, а иногда z , чтобы всегда получалось что-то меньшее 1.

Из условия 2						z		3 следует							2	1				и		z			1, то есть в знаменателе
															2							z

															z							3
															z							3
можно получать					2				и		z	, но нельзя						z			и		3		.
можно получать									и			, но нельзя									и				.
							z			3							2						z
	1	1	=						1					1			=		1					1				1		1
	z 2	z 3	=							2					z		=									2						z
	z 2	z 3								2					z				z							2	3					z
				z 1									3 1								1								1
				z 1									3 1								1								1
										z					3											z						3
теперь в каждом случае получено выражение вида																													1		котрое и


																												1 q

является суммой геометрической прогрессии, и его можно превратить

																				1
в бесконечную сумму по формуле																				1					q n .

																			1 q
																			1 q						n 0
																									n 0
1			1					1			1					1			2	n			1						z	n
													=																			=
	z			2				3				z				z n 0			z					3 n 0					3
		1							1
		1							1
				z								3
				2			n						z		n					2		2			2		1				1		z		z	2
( 1)n				2				( 1)n					z				=	...		2					2		1				1		z		z		...

					z	n 1							3	n 1							z	3			z	2							3	2	3	3
n 0					z					n 0			3								z				z			z 3					3		3

2) Теперь разложим в ряд во внешней области, которую, впрочем,

можно также считать кольцом типа 3

Здесь

3 причѐм

автоматически выполнено также и

2 , т.е. надо получать в

знаменталелях выражения

, и в итоге в ответе будут только

отрицательные степени.

z 2

z 3

z 1

136

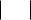
1	2	n	1


z n 0	z		z


	3		n
	3
		в данном случае их можно и объединить,
		в данном случае их можно и объединить,
n 0	z

т.к. в каждом слагаемом есть одинаковые степени.

1	2	n	3	n


z n 0	z		z

		n	3	n
= ( 1)n	2				. В этом ряде Лорана есть
		z n 1
n 0

только главная часть.

3) Если требуется разложить в ряд в круге, то это получится ряд Тейлора, там наоборот, в обеих дробях надо выносить константу,

чтобы было

1			1

z 2		z 3
	1		z n


	2 n 0		2

z	и			z	.
	и				.
3			2
=					1

						z
						z
		2 1
		2 1
						3
	1						z	n


	3 n 0						3

	1		=	1		1		1	1		=
		z		2			z	3		z

3 1					1				1

		3					2			3

	n	1	1
= ( 1)					n
				z		.

n 0	2n 1		3n 1

Пример (со сдвигом центра)

Разложить функцию	1	в ряд Лорана по степеням	z 1.

	(z 2)( z 3)

Решение. Центр в точке 1, тогда расстояние до ближайшей особой точки равно 3, а до второй 4. Получается, что кольцо, где будет ряд,

для этой задачи: 3 z 1 4 .

Разложение на простейшие дроби то же самое,

z 2

z 3

Но после этого надо отделить выражение z 1.

далее в соответствии с

z 2

z 3

(z 1) 3

(z 1) 4

неравенствами

z 1

3 надо вынести за скобку в одной

дроби константу, а в другой z 1.

137

1				1			=		1		1					1	1			=
							=										z 1			=
(z 1) 3				(z 1) 4				z 1 1					3			4 1	z 1
								z 1 1				z	1			4 1
												z	1					4
1		1			1				1						1				3 n		1	z 1 n
												=											.
z 1										z 1		=											.
z 1				3	4					z 1				z 1 n 0					z 1		4 n 0	4
	1					1
	1					1
			z 1							4

Объединить их нельзя, так как в одной части отрицательные степени, а в другой части положительные, это главная и правильная часть ряда соответственно.

§4. Ряды Фурье.

Скалярное произведение функций.

Вспомним скалярное произведение векторов (a, b) a1b1 ...anbn .

Для функций можно построить обобщение. Если заданы 2 функции f (x), g(x) , то очевидно, их можно умножить в каждой точке. Затем

все эти произведения надо проинтегрировать, так как точек на интервале бесконечное количество. Получается как бы бесконечное количество координат.

Итак, определим скалярное произведение пары функций на интервале

(a, b) по формуле: ( f , g) f (x)g(x)dx .

Можно считать, что это верно и на отрезке [a,b] , ведь две граничные точки не влияют на величину интеграла.

Пример. Найти скалярное произведение f (x) x и g(x) x 2 на интервале (0,1).

1	1	x	4	1	1

Решение. ( f , g) x x2 dx =	x3dx =					.
		4			4
0	0			0

Свойства скалярного произведения, которые легко следуют из свойств линейности интеграла:

( f , g) (g, f )

138

( f g, h) ( f , h) (g, h) , ( f , g h) ( f , g) ( f , h) (cf , g) c( f , g) , ( f , cg) c( f , g)

Вспомним, что для векторов есть понятие модуля,

a 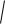a12 ...an 2 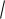(a, a) . Аналогичное понятие для функций называется нормой функции:

Очевидно, что этот квадратный корень существует, ведь f 2 (x) 0 , а

значит и f 2 (x)dx 0 .

Ортогональные функции.

Две функции называются ортогональными на интервале (a, b) , если

( f , g) 0 , то есть f (x)g(x)dx 0 .

Здесь нет такого простого геометрического смысла, как в случае перпендикулярных векторов, для функций ортогональность значит, что произведение функций где-то больше, а где-то меньше нуля так, чтобы эти части компенсировались и уничтожились при интегрировании.

Пример. Доказать, что функции f sin x , g cosx ортогональны на интервале (0, ) .

	1			1

sin x cos xdx =		sin 2xdx	=		cos2x
	2			4		0
0		0

= 14 (cos2 cos0) = 0.

Замечание. Если одна из функций в произведении тождественно равна 0, то интеграл очевидно, равен 0. Поэтому тождественный 0 это ортогональная всем функция.

Ортогональные системы. Если любая пара функций в системе ортогональна, то система называется ортогональной.

139

0 ,1 ,2 ,..., n , ,... ортогональна, если (i , j ) 0										для любых i j .
Система функций на отрезке [l, l]:
1		x		x		n x		n x
	,sin		, cos		,...,sin		, cos		,...
	,sin		, cos		,...,sin		, cos		,...
2		l		l		l		l

ортогональна, еѐ подробно рассмотри позже, с помощью неѐ как раз и строятся тригонометрические ряды Фурье.

Формулы коэффициента (Фурье) разложения по ортогональной

системе: с	( f ,n )	или с		( f , n )			.

n	(n ,n )	n			n	2

Доказательство. Пусть функция f						представлена в виде суммы:
f c0 0 c1 1 ...cn n ...			найдѐм коэффициенты .
Можно скалярно домножить на n . Получим
( f ,n ) (c0 0 c1 1		...cn n ..., n ) =

c0 (0 ,n ) c1 (1 ,n ) ...cn (n ,n ) ...

среди этих слагаемых, лишь одно отлично от нуля, ведь система

ортогональна, и при i n будет

(i ,n ) 0 .

Тогда ( f ,

) c

(

) , тогда

( f ,n )

то есть

( f , n )

(n ,n )

f (x) n (x)dx

Можно записать и с помощью интегралов: с

2 (x)dx

Аналогичное равенство верно и для векторов:

(a, e1 )

140

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 1814 15 16 17 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.20234.98 Mб6Математика для гуманитарных, экологических и экономико-юридических специальностей. Часть 2.pdf
#
05.02.202311.03 Mб10Математика-2-й семестр (курс лекций)..pdf
#
05.02.20234.95 Mб6Математика-3-й семестр(курс лекций)..pdf
#
05.02.20231.56 Mб4Математика. Дополнительные главы.pdf
#
05.02.2023984.92 Кб13Математика. Математический анализ.pdf
#
05.02.20232 Mб5Математика.-1.pdf
#
05.02.20232.61 Mб4Математика.-2.pdf
#
05.02.20232.05 Mб3Математика.-3.pdf
#
05.02.20232.49 Mб3Математика.-4.pdf
#
05.02.20233.03 Mб3Математика.-5.pdf
#
05.02.20232.78 Mб3Математика.-6.pdf