
Математика.-1
.pdf
1
Доказательство очевидно: они эквивалентны интегралам 1 x a dx , про
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
которые известно, что при a 1 есть сходимость. Итак, |
|
1 |
, |
1 |
, |
|||||||||
2 |
3 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
n 1 n |
n 1 n |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
сходятся, а вот |
1 |
, |
1 |
|
расходятся, здесь степень |
|
|
||||
3 |
|
|
|
|
|
|
|
|||||||
n 1 n |
2 |
n 1 n |
n 1 |
|
n |
|
|
|
|
|
|
|
||
меньше или равна 1.
Но не всегда удаѐтся подобрать такую функцию, чтобы применить интегральный признак Коши. Например, в ряде может содержаться n! Поэтому нужны и другие признаки.
Если исследовать внутреннюю структуру ряда, а именно отношение следующего слагаемого к предыдущему, то например, для геометрической прогресмсии это число всегда одно и то же q
(называется знаменатель прогрессии). А вот если ряд не является прогресией, то оно как-то варьируется, для сходимости важно, чтобы оно оказалось меньше какого-то q , то есть было меньше сходящейся прогрессии.
Теорема 3. Признак Даламбера в конечной (не-предельной) форме. Если при всех n n0 (то есть начиная с некоторого номера)
выполняется условие |
| an 1 | |
q 1 , то ряд абсолютно сходится. |
|
| an | |
|||
|
|
Доказательство. Во-первых, сходимость ряда равносильная сходимости его остатка, т.е. можем рассмотреть остаток ряда и заново перенумеровать члены ряда, начиная с n0 , поэтому можно доказывать
даже при том условии, что |
| an 1 | |
q 1 |
верно, даже начиная с |
|
|||
| an | |
|
||||||
|
|
|
|
|
|
||
первого номера. Обратите внимание, что условие |
| an 1 | |
q 1 |
это не |
||||
| an | |
|||||||
|
|
|
|
|
|
||
111

то же самое что |
| an 1 | |
1 . В нашем случае все они меньше q , |
|
| an | |
|||
|
|
которое само меньше 1, т.е. отделено от 1 некоторым расстоянимем на числовой прямой, т.е. предел этих величин не может быть равен 1, от любой из них до 1 остаѐтся некоторое расстояние (1 q) !
|
| a2 | |
q |
| a2 |
| q | a1 | , |
|
|
|
|
|
|||||||||||
|
| a1 | |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
| a3 | |
q | a |
|
| q | a |
|
| |
| a | q2 | a | . |
|
|
|
|
|||||||||
|
|
|
|
3 |
2 |
|
|
|
|
|||||||||||
|
| a2 | |
|
|
|
|
|
|
|
|
|
3 |
1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Продолжая таким образом, можно модуль каждого члена ряда |
|
|||||||||||||||||||
оценить с помощью | |
a1 | |
и какой-то степени числа q . |
|
|
||||||||||||||||
Итак, | a |
| | a |
2 |
| | a |
3 |
| ... | a |
| q | a | q2 |
| a | ... = |
|
|
|||||||||||
|
|
|
|
1 |
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|||||
| a | 1 q q 2 ... получилось, что ряд, состоящий из модулей, |
||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
меньше некоторой убывающей геометрической прогрессии. |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| a1 | 1 q q 2 ... | a1 | |
|
1 |
|
|||
|
|
an |
|
= | a1 | | a2 | | a3 |
| ... |
|
. |
|||||||||||||
|
|
|
||||||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
q |
|||||||||||||||||
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Итак, сумма меньше некоторого конечного числа, т.е. ряд an
n 1
сходится, а значит, исходный ряд сходится абсолютно.
Теорема 4. Признак Даламбера в предельной форме.
Если lim |
| an 1 |
| |
q 1 то ряд абсолютно сходится, если при этом |
|
|
|
|||
n |
| a |
n |
| |
|
|
|
|
|
|
q 1 то ряд расходится.
Доказательство. Следует из предыдущей теоремы таким образом. Если предел равен q и оно строго меньше 1, то для всякого 0 ,
112
начиная с некоторого номера, все отношения вида |
| an 1 |
| |
входят в |
| an | |
|
||
|
|
|
окрестность (q , q ) , а если заранее возьмѐм 1 q , то все эти элементы окажутся левее, чем q2 q , при этом q2 1.
То есть, они всѐ равно будут отделены от 1 неким расстоянием. А тогда выполняются условия прошлой теоремы, и ряд абсолютно сходится.
1
Пример. Исследовать сходимость ряда n .
n 1 3
Поделим n+1 й член ряда на n-й. На практике лучше пользоваться предельным признаком, т.е. сразу перейти к пределу и получить q .
|
| a |
n 1 |
| |
|
1 |
|
1 |
|
|
3n |
|
1 |
|
|
|
lim |
|
|
lim |
|
: |
|
= |
lim |
|
= |
|
|
1 |
. Ответ: ряд сходится. |
|
|
|
|
|
|
|
|
|
||||||||
n |
| an | |
|
n 3n 1 |
|
3n |
n 3n 1 |
|
3 |
|
|
|||||
Замечание. Сходимость здесь сразу абсолютная, так как все слагаемые и так положительны.
1
Пример. Исследовать сходимость ряда .
n 1 n!
|
|
| a |
n 1 |
| |
|
1 |
|
|
1 |
|
|
n! |
|
|
|
1 2 ... n |
|
|||
lim |
|
|
lim |
|
|
: |
|
|
= |
lim |
|
|
= |
lim |
|
|
= |
|||
n | an | |
|
|
(n 1)! |
|
|
|
|
n (n 1)! |
|
n 1 2 |
... n (n 1) |
|
||||||||
|
n |
|
n! |
|
|
|
||||||||||||||
lim |
|
1 |
|
0 . Итак, q 0 |
1, ряд сходится. |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
n n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Замечание. Если было бы знакочередование, для признака Даламбера всѐ равно надо было бы рассмотреть по модулю, т.е. отбросить ( 1) n .
|
( 1)n |
|
|
n! |
|
n 1 |
|
тоже сходится абсолютно. Знакочередование - вовсе не |
|
|
|
значит, что сходимость условная. Если исследовать здесь ряд даже без знакочередования, то он сходится.
113

Теорема 5. Радикальный признак Коши в конечной форме.
|
|
|
|
|
|
|
|
|
|
|||
Если при всех n n |
0 |
выполнено условие |
n | a |
n |
| q 1, то ряд |
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
an абсолютно сходится. |
|
|
|
|
|
|
|
|
|
|||
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| qn . Таким образом, |
||||
Доказательство. Если n | a |
n |
| q , то |
| a |
n |
||||||||
|
|
|
|
|
|
|
|
|
|
|||
начиная с некоторого номера, остаток ряда меньше или равен, чем убывающая геометрическая прогрессия.
| a | | a |
|
| | a |
|
|
| ... |
q q 2 q3 ... |
|
q |
. Эта сумма конечна, то |
||||
2 |
3 |
|
|
||||||||||
|
|
||||||||||||
1 |
|
|
|
|
|
|
1 |
q |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
есть ряд абсолютно сходится. |
|
|
|||||||||||
Теорема 6. Радикальный признак Коши в предельной форме. |
|||||||||||||
|
|
|
|
|
|
|
|||||||
Если |
lim n | a |
n |
| q 1 |
то ряд абсолютно сходится, если q 1 |
|||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
расходится.
Доказательство следует из предыдущей теоремы, аналогично тому, как Т.4 из Т.3.
|
|
|
|
|
|
|
|
|
|
|
1 |
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример. Выяснить сходимость ряда 1 |
|
|
. |
|
|||||||||||
|
|
||||||||||||||
|
|
|
|
|
|
|
|
n 1 |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
n2 |
|
|
|
|
|
|
n |
|
|
|
|
|
|
1 |
n |
|
|
|
|
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|||||||
Рассмотрим lim |
n | an | lim 1 |
|
|
|
= lim 1 |
|
|
e 1 |
|||||||
|
|
||||||||||||||
n |
|
|
n |
|
n |
n |
|
|
n |
|
|
||||
(использовали 2-й замеч. предел) ряд расходится.
Замечание. При q 1 признак Даламбера и радикальный признак
Коши не дают никакого ответа, в этом случае надо применять какиелибо другие признаки.
114
ЛЕКЦИЯ № 11. 25. 04. 2017
Далее следует серия признаков, основанных не на внутренней структуре ряда, а на сравнении с каким-то внешним, «эталонным» рядом.
Теорема 7. Признак сравнения в конечной форме.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Даны 2 ряда, |
an |
и |
bn , причѐм, |
начиная с какого-то номера n0 |
||||||||||||||
|
n 1 |
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
||||
верно an bn . Тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1) Из сходимости bn следует сходимость an , |
||||||||||||||||||
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
n 1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2) Из расходимости an |
следует расходимость bn . |
|||||||||||||||||
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
n 1 |
||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||
Пример. Выяснить сходимость |
|
|
|
|
|
. |
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
n |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
n 3 2 |
|
ln n |
||||||||
Заметим, что |
1 |
|
|
1 |
при n 3 , |
так как ln n ln e 1. |
||||||||||||
|
|
|
2n |
|||||||||||||||
|
|
2n ln n |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
В то же время ряд |
, с помощью которого мы ограничили сверху, |
|||||||||||||||||
n |
||||||||||||||||||
|
|
|
n 3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
это сходящаяся геометрическая прогрессия, поэтому тот исходный |
||||||||||||||||||
ряд тоже сходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Теорема 8. Признак сравнения в предельной форме. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
an |
|
|
|||||
Даны 2 ряда, |
an |
и |
bn , причѐм lim |
|
C , где C константа, |
|||||||||||||
|
|
|||||||||||||||||
|
n 1 |
|
|
n 1 |
|
n b |
n |
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
C 0, , т.е. an , bn - бесконечно малые одного порядка, тогда ряд |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
an сходится тогда и только тогда, |
когда bn сходится. |
|||||||||||||||||
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|||||
Пример. Выяснить, сходится ли ряд |
|
|
. |
|||||||||||||||
n3 2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
115

Пусть a |
|
|
|
|
n 1 |
, |
тогда возьмѐм b |
||||||
n |
|
|
|
||||||||||
|
|
|
|
|
n3 2 |
|
|
|
n |
||||
|
|
|
|
|
|
|
|
|
|
||||
этих величин равен 1. |
|
|
|
||||||||||
n 1 |
|
|
1 |
|
|
(n 1)n |
2 |
|
|||||
lim |
|
|
|
|
: |
|
= |
lim |
|
|
= lim |
||
|
|
|
|
|
|
|
|||||||
n n3 2 |
|
|
n2 |
|
n n3 2 |
|
n |
||||||
n |
|
1 |
. Предел отношения |
|
n3 |
n2 |
|||
|
|
n3 n 2 1. n3 2
|
|
|
|
|
|
|
|
|
1 |
|
Поэтому для исследования сходимости, можно рассматривать |
||||||||||
2 |
||||||||||
|
|
|
|
|
|
|
|
n 1 n |
||
|
|
|
|
n 1 |
|
|||||
вместо |
|
|
|
, они эквивалентны в смысле сходимости. В то же |
||||||
n3 |
2 |
|||||||||
|
|
n 1 |
|
|
|
|
|
|
||
|
|
|
1 |
|
|
|
|
|||
время |
|
|
уже легко сравнить с несобственным интегралом |
|
||||||
|
2 |
|
|
|||||||
|
|
n 1 n |
|
|
|
|||||
|
1 |
|
|
|
|
|
|
|
|
|
|
dx , который в свою очередь сходится. Ответ: ряд сходится |
|
||||||||
2 |
|
|||||||||
1 |
x |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
(абсолютно, т.к. слагаемые все положительны).
Теорема 9. Признак Лейбница. Если выполнены 2 условия: 1) Ряд знакочередующийся, 2) an монотонно убывает к нулю.
|
|
|
Тогда ряд an сходится. |
|
|
n 1 |
|
|
Идея доказательства. У нас есть ряд вида a1 a2 |
a3 a4 |
... |
Сначала объединим так: (a1 a2 ) (a3 a4 ) ... в каждой скобке положительное число, так как вычитаемое меньше по модулю, из-за
монотонности. |
Получается, |
что |
подпоследовательность |
в |
|
последовательности частичных сумм возрастает. |
|
|
|||
А теперь перегруппируем так: |
|
a1 (a2 a3 ) (a4 |
a5 ) ... |
из |
|
элемента a1 вычитаются какие-то положительные числа, то есть частичный суммы меньше, чем a1 . Итак, последовательность
частичных сумм монотонно возрастает и ограничена сверху, а значит, у неѐ есть предел. тогда ряд сходится.
116
|
1 |
|
1 |
|
|
1 |
|
1 |
|
( 1) |
n 1 |
|
Пример. 1 |
|
|
|
|
... = |
|
условно сходится. |
|||||
2 |
3 |
4 |
5 |
n |
|
|||||||
|
|
|
|
n 1 |
|
|
||||||
§2. Функциональные ряды.
Ряд вида fn (x) называется функциональным рядом.
n 1
Для функций комплексного переменного fn (z) .
n 1
Если фиксировать ту или иную точку из области определения, будет получать различные числовые ряды. Фактически, здесь имеется бесконечное множество числовых рядов, так как бесконечное множество точек в области определения.
Например, рассмотрим ряд x x2 x3 ... мы можем зафиксировать различные точки, и будем получать различные числовые ряды:
x 0 |
|
0 0 0 ... сходится, сумма равна 0. |
|||||||
x 1 |
1 1 1 ... расходится, сумма . |
||||||||
x |
1 |
|
1 |
|
1 |
|
1 |
... сходится, это геометрическая прогрессия, |
|
|
|
|
|
|
|||||
2 |
|
2 |
4 |
8 |
|
||||
сумма равна 1.
Область сходимости функционального ряда.
Определение. Множество D называется областью сходимости, если
для каждой точки z0 D соответствующий числовой ряд f n (z0 )
n 1
сходится.
Если ряды из комплексных функций, то D это область в плоскости, например круг, а если действительные функции, то D какой-либо интервал или объединение интервалов на действительной прямой.
Метод нахождения области сходимости. применять те же самые признаки (Даламбера, Коши) но только для «произвольного» x .
117
То есть, в пределе так до конца и остаѐтся переменная. а затем решить неравентво.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
Пример. Найти область сходимости ряда |
x |
. |
||||||||||||||||||||||||||||||
n |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
2 |
|
|
|
x |
|
n 1 |
|
|
x |
|
n |
|
|
|
x |
|
n 1 |
2 |
n |
|
|
|
x |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
lim |
|
|
|
|
: |
|
|
|
|
= |
lim |
|
|
|
|
|
|
= |
|
|
|
|
q(x) < 1. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
n |
|
2n 1 |
|
|
2n |
|
n |
2 |
n 1 |
|
x |
|
n |
|
|
2 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Если раньше, в теме «числовые ряды» мы просто получали в пределе какое-то число q и могли сказать, что оно больше либо меньше 1, то
теперь получили функцию от x , т.е. при одних значениях больше 1, а при других меньше. Надо решить неравенство и найти, где это выражение меньше 1.
x |
|
1 |
|
|
x |
|
2 |
x ( 2,2) это интервал, где есть абсолютная |
|
|
|
|
|||||||
|
|||||||||
2 |
|
||||||||
|
|
|
|
|
|
|
|
сходимость.
Там, где q(x) 1, то есть x ( , 2) (2, ) ряд расходится. При q(x) 1 признак Даламбера не даѐт ответа, надо проводить
исследование поведения ряда в граничных точках в ручном режиме.
|
|
n |
|
|
|
|
Подставим x 2 . Получим ряд |
2 |
1 он расходится. |
||||
|
n |
|||||
n 1 |
2 |
n 1 |
|
|||
|
|
( 2) |
n |
|
||
Подставим x 2 . Получим ряд |
|
|
( 1)n он тоже |
|||
|
|
|
||||
n 1 |
2n |
|
|
n 1 |
||
расходится, не выполнен необходимый признак, т.е. слагаемые не
уменьшаются к 0. Итак, граничные точки не добавятся к области сходимости, и ответ остаѐтся таким: x ( 2,2) .
Пример. Найти область сходимости ряда
|
|
|
x |
|
n 1 |
|
|
x |
|
n |
|
|
|
|
|
x |
|
n 1 |
n |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
lim |
|
|
|
|
: |
|
|
|
|
= lim |
|
|
|
|
|
|
= |
|
x |
|
lim |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
n n |
|
1 |
|
|
n |
|
n |
|
x |
|
n |
(n 1) |
|
|
|
|
n |
|||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
||||||||
|
x |
|
. |
|
|
|
|
||
|
|
|
|||||||
n 1 n |
|||||||||
n |
= |
|
x |
|
. |
||||
|
|
||||||||
|
|
|
|
||||||
n 1 |
|||||||||
|
|
|
|
|
|
||||
118

Теперь решим неравенство x 1. Это означает x ( 1,1) - вот
область абсолютной сходимости. Исследуем граничные точки.
|
|
|
|
|
|
|
|
|
При x 1: ряд |
1 |
, он расходится (гармонический ряд, изучали |
||||||
|
||||||||
|
n 1 n |
|
|
|
|
|
|
|
|
|
|
|
|
( 1)n |
|
||
|
x 1: ряд |
|
n |
|
||||
ранее). При |
n 1 |
|
, знакочередующийся, сходится по |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
признаку Лейбница, но условно, так как |
1 |
это и есть ряд из его |
||||||
|
||||||||
|
|
|
|
|
|
n 1 n |
|
|
модулей а он расходится. итак, ответ: область сходимости x [ 1,1) .
|
|
|
|
|
|
|
(x 1) |
n |
|
|
|
|
|
|
|
|||
Пример. Найти область сходимости |
|
|
. |
|
|
|
|
|
|
|
||||||||
|
2n |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Извлечѐм корень n порядка из модуля. Получим |
|
|
x 1 |
|
|
. |
||||||||||||
|
|
|||||||||||||||||
|
|
|||||||||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||
|
|
|
x 1 |
|
|
1 , т.е. |
|
|
|
|
||||||||
Решим неравенство |
|
|
|
|
x 1 |
|
2 , |
что равносильно |
||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|||||||||||||||||
|
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 x 1 2 , то есть |
|
1 x 3 . |
Решением |
неравенства будет |
||||||||||||||
множество ( 1,3) . Подставляя граничные точки, получаем расходимость:
|
|
2 |
n |
|
2 |
n |
|
|
При x 3: |
|
|
|
|
1 |
|||
(3 1)n |
2n |
|||||||
|
n 1 |
n 1 |
n 1 |
|||||
слагаемые не стремятся к 0, не выполнен необходимый признак, ряд расходится.
|
|
2 |
n |
|
2 |
n |
|
|
При x 1: |
|
|
|
|
( 1)n по той же причине ряд |
|||
( 1 1)n |
( 2)n |
|||||||
|
n 1 |
n 1 |
n 1 |
|||||
расходится.
Ответ. область сходимости ( 1,3) .
119
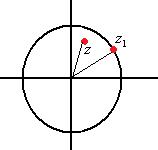
§3. Степенные ряды.
|
|
Общий вид степенного ряда: an (z z0 )n , где an числовые |
|
n |
0 |
коэффициенты. В этом ряде только положительные степени одного и того же выражения (z z0 ) и константа (что получается при нулевой
степени). Возможно, что часть коэффициентов равна 0, то есть некоторые степени пропущены.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема 1 (Абеля). 1) Если ряд an zn |
|
сходится в точке z1 , то он |
||||||||||||||
|
|
|
|
|
|
|
|
n 0 |
|
|
|
|
|
|
|
|
сходится в любой точке z , для которой |
|
z |
|
|
|
z1 |
|
, причѐм абсолютно. |
||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) Если ряд an zn |
|
расходится в точке z1 то он расходится в любой |
||||||||||||||
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
точке, для которой |
|
z |
|
|
|
z1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство. Сходимость в точке z1 |
|
ряда an zn означает, что |
||||||||||||||
n 0
an z1n С . Если этот ряд сходится, то согласно необходимому
n 0
признаку, слагаемые стремятся к 0. Тогда среди них есть максимальное по модулю, и таким образом, они ограничены в
совокупности, некоторой константой M , т.е. |
a |
z n |
M . |
|
|
n 1 |
|
|
|
|
|
Теперь рассмотрим ряд an zn в произвольной точке z , которая |
|||
n 0 |
|
|
|
ближе к началу координат на комплексной плоскости.
120
