
Дополнительные главы математики
..pdf
X ( p) |
1 |
||
2 |
|
||
( p 1) |
( p 2) |
||
|
|||
кратности больше 1.
отличие в том, что здесь возникает полюс
e2t
1
|
|
e |
pt |
|
|||
Re s |
|
|
|
||||
( p 1) |
2 |
( p |
|||||
|
|
||||||
|
|
|
|
||||
|
te pt ( p 2) e |
||||||
|
( p 2) |
2 |
|||||
|
|
||||||
=
2)
pt
p 1
e |
pt |
|
|
|
|
|
|
( p 1) |
2 |
||
|
|||
= e |
2t |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
p 2 |
|
||
te |
t |
( 1) |
|
|
|||
|
|
|
1 |
e |
pt |
|
et
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
p 1 |
||
|
|
||
= e |
2t |
||
|
|||
=
e |
t |
|
tet
.
Ответ.
x(t) e |
2t |
e |
t |
|
|
te |
t |
|
.
Задача 70.
уравнение
Решить линейное неоднородное дифференциальное
|
1. |
x x cost с условиями Коши x(0) 2, x (0) |
Решение.
p pX ( p)
p pX ( p) x(0) x (0) |
|||
2 1 X ( p) |
p |
||
2 |
1 |
||
p |
|||
|
|||
X
( p) |
|
( p |
2 |
|
|
|
p |
|
p |
2 |
|
|
||
1) X ( |
||
|
|
|
|
|
1 |
|
|
|
|
p) |
p |
2 p 1 |
||
2 |
1 |
|||
p |
|
|||
|
|
|||
X ( p) |
|
|
p |
|
|
2 p 1 |
. Обратное преобразование Лапласа можно |
|||
( p |
2 |
1) |
2 |
p |
2 |
1 |
||||
|
|
|
||||||||
|
|
|
|
|
|
|||||
найти отдельно для каждого слагаемого (вследствие линейности).
|
|
|
|
|
|
pe |
pt |
|
|
|
|
|
|
|
pe |
pt |
|
|
||||||
Для 1-го: Re s |
|
|
|
|
|
Re s |
|
|
= |
|||||||||||||||
( p i) |
2 |
( p i) |
2 |
( p i) |
2 |
( p i) |
2 |
|||||||||||||||||
|
|
|
|
p i |
|
|
p i |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
p |
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
pt |
|
|
|
|
|
|
|
|
|
|
pt |
|
|
|
|
|
|
|
||
|
( p i) |
2 e |
|
|
|
( p |
i) |
2 |
|
e |
|
|
= |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
p i |
|
|
|
|
|
|
|
|
|
|
p i |
|
|
|
|
|
||
71
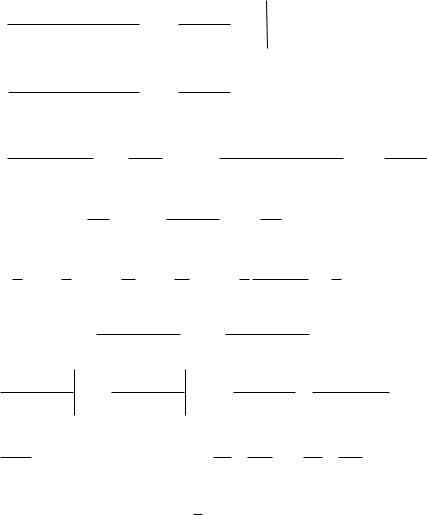
1( p i) |
2 |
|
2( p |
i) p |
|
|
|
|||||||||||
|
|
|
e |
pt |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
( p i) |
4 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1( p i) |
2 |
|
2( p |
i) p |
|
|
|
|||||||||||
|
|
|
e |
pt |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
( p i) |
4 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
(2i) |
2 |
2(2i)i |
|
|
|
|
|
i |
|
|
||||||||
|
e |
it |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
(2i) |
4 |
|
|
|
|
|
|
|
|
2 |
|||||||
|
|
|
|
|
|
|
|
(2i) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
4 4 |
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|||
e |
it |
|
|
|
|
te |
it |
|
+ |
|
||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
||||||||
(2i) |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
p |
|
|
|
|
|
|
|
|
te |
pt |
|
+ |
( p i) |
2 |
|
|
|||
|
|
|
|
|
p i |
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
te |
pt |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|||||
( p i) |
2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
p i |
|
|
||||||
|
|
|
|
|
|
( 2i) |
2 |
2( 2i |
||||||
te |
it |
|
+ |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
( 2i) |
4 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
( 4) 4 |
e |
it |
|
i |
te |
it |
||||||||
|
|
|
|
|
|
|
|
|||||||
( 2i) |
4 |
|
|
4 |
|
|||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
)(i) |
|
it |
|
i |
|
|
it |
|
|
|
|
e |
|
|
|
te |
|
||
|
|
|
|
2 |
|
||||
|
|
|
|
|
( 2i) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=
i teit
4
i |
te |
it |
|
||
4 |
|
|
|
|
=
1 |
te |
it |
|
||
4i |
|
|
|
|
1 |
te |
it |
|
||
4i |
|
|
|
|
=
t |
e |
it |
e |
|
|||
2 |
|
|
2i |
it
=
t |
sin t |
|
2 |
||
|
.
Для 2-го:
(2 p 1)e p i
Re s
p i
pt
p i
(2 p 1)e |
pt |
|
|
|
|
||
( p i)( p i) |
|||
|
(2 p 1)e |
pt |
|
|
|
||
p i |
|
|
|
|
|
|
|
p
Re s |
( |
p i |
|
= |
|
i |
|
(2 p 1)e |
pt |
|
|
||
p i)( p i) |
||
(2i 1)e |
it |
|
|
|
|
2i |
|
|
|
|
|
=
( 2i 1)e2i
it
=
2ieit
2i
Ответ.
Задача
2ie |
it |
|
e |
it |
|
e |
it |
|
|
|
e |
it |
|
e |
it |
|
|
|
e |
it |
|
e |
it |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2cost |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
= 2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
2i |
|
2i |
|
2i |
|
|
|
2 |
|
|
2 |
|
2i |
|
2i |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x(t) |
2 cos t sin t |
t |
sin t . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
71. Решить линейное неоднородное дифференциальное
sin
t
.
уравнение x 2x 2x 10e2t с условиями Коши
x(0)
0 ,
x (0)
0
.
Решение. Преобразуем левую и правую часть. |
|
|
p pX ( p) x(0) x (0) 2 pX ( p) x(0) 2X ( p) |
10 |
|
|
||
p 2 |
72
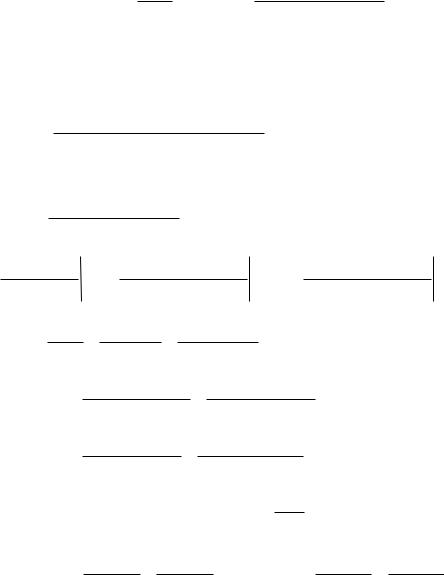
p |
2 |
2 p 2 X ( p) |
10 |
|
|||
|
p 2 |
||
|
|
|
X ( p) |
p |
|
10 |
|
2 |
2 p 2 ( p 2) |
|||
|
||||
|
|
.
Первый множитель знаменателя не имеет действительных корней.
D 4
X ( p)
8 4 , корни |
p |
2 2i |
1 i |
|
2 |
||||
|
|
|
||
|
10 |
|
|
|
( p ( 1 i))( p ( 1 i))( p 2) |
||||
Найдём обратное преобразование с помощью суммы вычетов.
Re s |
p |
|
|
10e |
||||
2 |
2 p |
|||||||
|
|
|
||||||
|
|
|
|
|||||
|
|
10e |
pt |
|
|
|
|
|
|
|
|
|
|
|
|
||
p |
2 |
2 p |
2 |
|||||
|
||||||||
|
p 2 |
|||||||
|
|
|
|
|
|
|
||
pt |
|
= |
|
2 ( p 2) |
|
10e |
pt |
|
|
( p ( 1 i))( p 2) |
|
|
|
10e |
pt |
|
|
|
|
|
( p ( 1 i))( p 2) |
||
p 1 i |
|
||
|
|
|
|
=
p 1 i
10e |
2t |
|
10e |
t |
e |
it |
|
10e |
t |
e |
it |
|
|
|
|
|
|
|
|
||||||
10 |
2i( 3 i) |
( 2i)( 3 i) |
||||||||||
|
|
|||||||||||
=
e
e
2t
2t
|
|
2t |
|
( 3 i)10e |
t |
e |
it |
|
|
( 3 i)10e |
t |
e |
it |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
e |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
2i( 3 i)( 3 i) |
2i( 3 i)( 3 i) |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
2t |
|
( 3 i)10e |
t |
e |
it |
|
( 3 i)10e |
t |
e |
it |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
e |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2i 10 |
|
|
|
|
|
|
|
|
|
2i 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
t |
|
3e |
it |
|
|
|
|
3e |
it |
|
|
ie |
it |
|
|
ie |
it |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
e |
2t |
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
2i |
|
|
|
|
2i |
|
|
2i |
|
|
|
2i |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
t |
|
|
e |
it |
e |
it |
|
|
|
e |
it |
|
e |
it |
|
|
|
|
|
|
|
|
t |
|
|
e |
it |
e |
it |
|
e |
it |
e |
it |
|
||||||
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= e |
2t |
e |
|
3 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
3 |
|
|
|
2i |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2i |
|
|
|
2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
e t 3sin t cost . |
|
|
|
Ответ. |
|
e2t e t 3sin t cost . |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
=
73
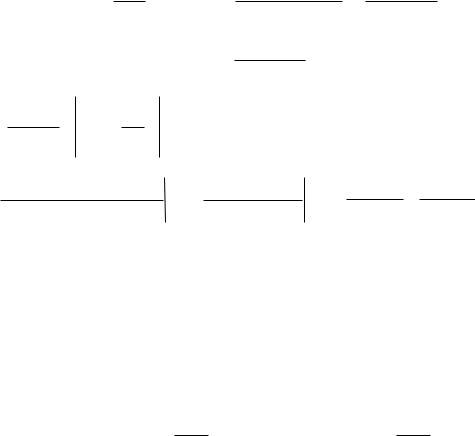
Задача 72. Решить линейное неоднородное дифференциальное
уравнение 3 порядка |
|
x |
|
e |
t |
с условиями Коши |
x |
|
|
x(0) 0, x (0) 0, x (0) 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решение. Так как условия Коши нулевые, то сразу запишем |
|
|||||||||||||||||
p |
3 |
p |
2 |
X ( p) |
|
1 |
|
X ( p) |
|
|
1 |
|
= |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
p 1 |
( p |
3 |
p |
2 |
)( p 1) |
p |
2 |
( p 1) |
2 |
|||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
.
Обратное преобразование:
Re s |
|
|
e |
pt |
|
|
|
|
|
|
|||
p |
2 |
( p 1) |
2 |
|||
|
||||||
|
|
|
||||
=
|
e |
pt |
|
|
|
||||
|
|
|
|
|
|
( p 1) |
2 |
|
|
|
|
|
||
p 0
e |
pt |
|
|
||
|
|||||
|
|
|
2 |
|
|
|
p |
|
|
||
|
|
|
|
||
p 1
=
te |
pt |
( p 1) |
2 |
2( p 1)e |
pt |
|
te |
pt |
p |
2 |
|
2 pe |
pt |
||
|
|
|
|
|
|
|
|||||||||
|
|
( p 1) |
4 |
|
|
|
|
|
p |
4 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
p 0 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=
p 1
t 2( 1) |
|
te |
t |
|
2e |
t |
|
|
|
||||
1 |
|
|
1 |
|
|
|
|
|
|
|
|
=
t 2 tet
2et
.
Ответ.
x(t) t 2 te |
t |
|
2e |
t |
|
.
Задача 73.
уравнение
Решение.
p pX ( p)
Решить линейное неоднородное дифференциальное
x x e |
3t |
с условиями Коши x(0) |
3, x (0) |
1 . |
|
p pX ( p) x(0) x (0) X ( p) |
1 |
|
|
|
|
|||||
|
|
|
|
|||||||
p 3 |
|
|
||||||||
3 1 X ( p) |
1 |
|
p |
2 |
1 X ( p) 3 p 1 |
|
1 |
|||
|
|
|||||||||
p 3 |
|
p 3 |
||||||||
|
|
|
|
|
|
|
|
|
||
74
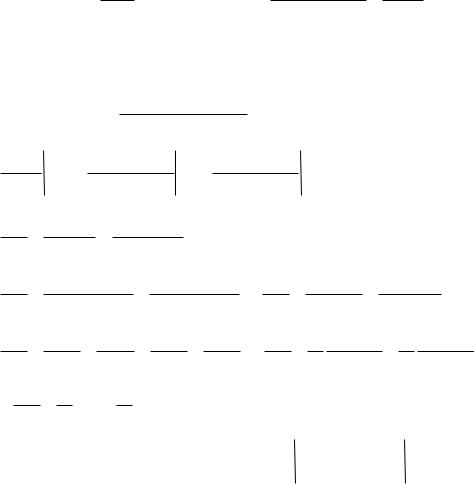
p |
2 |
1 X ( p) |
1 |
3 p 1 |
|
||||
|
p 3 |
|||
|
|
|
|
X ( p) |
1 |
|
|
|
3 p 1 |
|||
( p 3)( p |
2 |
1) |
p |
2 |
1 |
|||
|
|
|||||||
|
|
|
|
|||||
.
Обратное преобразование можно найти для каждого слагаемого по отдельности, и затем сложить результаты.
|
|
|
|
|
|
|
|
Re s |
|
|
|
|
e |
pt |
|
|
|
|
|
|
|
|
|||||||||
Для 1-го: |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|||||||||||||||
|
|
|
3)( p i)( p i) |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
( p |
|
|
|
|
||||||||||||||
|
e |
pt |
|
|
|
|
|
|
|
|
e |
pt |
|
|
|
|
|
|
|
|
|
|
e |
pt |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
p |
2 |
1 |
|
|
|
( p 3)( p i) |
|
|
|
|
( p 3)( p i |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
p 3 |
|
p i |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
e |
3t |
|
|
e |
it |
|
|
|
|
|
|
e |
it |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|||||||
10 |
(3 i)2i |
(3 i)( 2i) |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
e |
3t |
|
|
(3 i)e |
it |
|
|
|
|
|
|
(3 i)e |
it |
|
|
e |
3t |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
||||||||||||||||||
10 |
(3 i)(3 i)2i |
(3 i)(3 |
i)2i |
|
10 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
e |
3t |
|
3e |
it |
|
3e |
it |
|
|
|
|
ie |
it |
|
|
ie |
it |
|
|
|
e |
3t |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
||||||||||||||
10 |
10 2i |
10 |
2i |
|
10 |
2i |
10 2i |
|
10 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
e |
3t |
|
3 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= |
|
|
|
sin t |
|
|
cos t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
10 |
|
10 |
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Для 2-го: Re s |
|
(3 p 1)e pt |
|
|
= |
(3 p 1)e pt |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
( p i)( p i) |
|
|
|
p i |
|
|||||||||||||
) |
= |
|
p i |
||
|
|
(3 i)e |
it |
|
(3 i)e |
it |
|
|||||||
|
|
|
|
|
= |
||||||||
10 2i |
|
|
10 |
2i |
|||||||||
|
|
|
|
|
|||||||||
|
3 |
e |
it |
e |
it |
|
1 |
e |
it |
e |
|||
|
|
|
|
|
|
||||||||
10 |
|
|
2i |
|
|
10 |
|
|
|
2 |
|||
|
|
|
|
|
|
|
|
|
|||||
|
(3 p 1)e pt |
= |
|
p i |
|||
p i |
p i |
||
|
it
( 1 3i)eit |
|
( 1 3i)e it |
|||||
|
2i |
|
|
2i |
|
||
|
|
|
|
|
|||
|
eit e it |
|
3 |
eit |
e it |
= |
|
2i |
|
2 |
|||||
|
|
|
|
|
|||
= eit
2i
sin t
|
e it |
|
3ieit |
3ie |
it |
|
|
|
2i |
|
|
|
2i |
= |
|
|
|||||||
|
|
2i |
|
||||
3cost . |
|
|
|
|
|
|
|
75

|
|
|
|
e |
3t |
|
|
В сумме, |
|
|
|||||
10 |
|||||||
|
|
|
|
|
|||
1 |
e |
3t |
|
7 |
sin t |
||
|
|
||||||
10 |
|
|
|||||
|
|
|
10 |
|
|||
Ответ. x(t) 101
3 |
sin t |
1 |
||||
|
|
|
||||
10 |
|
|
10 |
|||
|
|
29 |
cos t . |
|||
10 |
||||||
|
|
|
|
|||
e 3t |
|
7 |
sin |
|||
|
||||||
|
|
|
10 |
|
||
cos t
t 1029
sin t
cos t
3cost
.
=
Задача 74. Решить линейное однородное дифференциальное
уравнение
y 10 y 9 y 0
с условиями Коши
y(0)
1, y (0)
7
.
Решение. Найдём преобразование Лапласа левой и правой части.
p( pY ( p) y(0)) y (0) 10( pY ( p) y(0)) 9Y ( p) 0 |
|
|
|
|
|
|||||||||||||||||
p( pY ( p) 1) 7 10( pY ( p) 1) 9Y ( p) 0 |
|
|
|
|
|
|
|
|||||||||||||||
p 2 10 p 9 Y ( p) p 7 10 0 |
|
p 2 10 p 9 Y ( p) 17 p |
||||||||||||||||||||
Y ( p) |
|
|
|
17 p |
|
|
= |
|
17 p |
. Обратное преобразование: |
||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||
|
|
p |
10 p 9 |
|
( p 1)( p 9) |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Re s |
|
(17 p)e pt |
|
это суммы вычетов в полюсах |
p 1 |
и p 9 . |
||||||||||||||||
|
( p 1)( p 9) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
(17 p)e pt |
|
|
(17 p)e pt |
16e pt |
|
8e pt |
= 2e |
t |
e |
9t |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
. |
|||||
p |
9 |
|
|
1 |
|
|
p 1 |
8 |
|
8 |
|
|
|
|||||||||
|
p |
|
|
|
p 9 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ. |
|
y e |
9t |
|
2e |
t |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
76
Задача 75. Решить линейное однородное дифференциальное
уравнение |
|
y |
|
|
3y |
|
2 y |
|
0 |
с условиями Коши |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
5 . |
|
|
|
|
|
|
|
|
||||||
y(0) 4, y (0) |
3, y (0) |
|
|
|
|
|
|
|
|
||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
p p( pY( p) y(0)) y (0) y (0) 3 p( pY ( p) y(0)) y (0) 2( pY( p) y(0)) 0 |
|||||||||||||||||||||||||||
|
|
p p( pY ( p) 4) 3 5 3 p( pY ( p) 4) 3 2( pY ( p) 4) 0 |
|
||||||||||||||||||||||||
( p |
3 |
3 p |
2 |
2 p)Y ( p) 4 p |
2 |
3 p 5 12 p 9 |
8 0 |
|
|||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||
( p3 3 p 2 2 p)Y ( p) 4 p 2 9 p 4 |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
4 p |
2 |
9 p 4 |
|
|
|
4 p |
2 |
9 p 4 |
|
4 p |
2 |
9 p 4 |
|
|||||||||||
Y ( p) |
|
= |
|
|
|
= |
|
|
|||||||||||||||||||
|
|
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||
|
|
|
p |
3 p |
2 p |
|
|
p( p |
3 p 2) |
p( p 1)( p 2) |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
обратное преобразование:
Re s |
(4 p |
2 |
9 p 4)e |
pt |
|
|
|
||||
p( p 1)( p 2) |
|||||
|
|||||
=
(4 p |
2 |
9 p 4)e |
pt |
|
(4 p |
2 |
9 p 4)e |
pt |
|
(4 p |
2 |
9 p 4)e |
pt |
|
|
|
|
|
|
|
|
||||||
( p 1)( p 2) |
|
|
|
p( p 2) |
|
|
|
p( p 1) |
|
||||
|
p 0 |
|
|
|
p 1 |
|
|
p 2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
4 |
|
4 9 4 |
e |
t |
|
16 18 4 |
e |
2t |
= 2 e |
t |
e |
2t |
. |
||
|
|
|
|
|
|||||||||||
|
1( 1) |
|
|
|
|
|
|
||||||||
( 1)( 2) |
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
Ответ. |
y 2 e |
t |
e |
2t |
. |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||||
Задача 76. Решить линейное однородное дифференциальное
уравнение |
y 9 y 0 |
с условиями Коши y(0) 2, y (0) 0 . |
=
Решение. p( pY ( p) y(0)) y (0) 9Y ( p) 0
77

p( Y (
pY ( p) 2) 9Y ( p)
p) |
2 p |
. |
||
( p 3)( p |
||||
|
3) |
|||
|
2 pe |
pt |
|
|
Re s |
|
|
||
( p 3)( p |
3) |
|||
|
||||
|
0 |
|
( p |
2 |
9)Y ( p) 2 p |
|
|
|
|
|
|||||
|
|
|
|
|
|||||||||||
Обратное преобразование: |
|
|
|
|
|
||||||||||
|
2 pe |
pt |
|
|
|
2 pe |
pt |
|
|
6e |
3t |
|
6e |
pt |
|
= |
|
|
|
|
|
|
= |
|
|
|
|||||
|
p 3 |
|
|
p 3 |
|
6 |
6 |
||||||||
|
|
p |
3 |
|
p 3 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
=
e |
3t |
|
e |
3t |
|
. Ответ. y e3t e 3t .
Задача 76-Б. Решить линейное неоднородное дифференциальное уравнение y 9 y et с условиями Коши y(0) 0, y (0) 0 .
Решение. В отличие от прошлой задачи, здесь есть функция в правой части, но нулевые условия Коши. Посмотрим, как это отразится на
решении.
p( pY ( p) y(0)) y (0) 9Y ( p) |
1 |
|
p 1 |
||
|
( p |
2 |
9)Y ( p) |
1 |
|
|||
|
p 1 |
||
|
|
|
Y ( p) |
1 |
|
( p 1)( p 3)( p 3) |
||
|
Re s |
|
|
|
e |
pt |
|
|
||||
|
|
|
|
|
|
||||||
( p |
1)( p 3)( |
||||||||||
|
|
|
|
||||||||
|
e |
pt |
|
|
|
|
|
e |
pt |
||
|
|
|
|
|
|
|
|
|
|||
p |
2 |
9 |
|
|
( p 1)( p |
||||||
|
|
|
|||||||||
|
p 1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|||
et |
|
e3t |
|
|
e 3t |
|
|
||||
8 |
2 |
6 |
( 4)( 6) |
||||||||
|
|
||||||||||
|
= |
|
|
|
|
|
|
|
|
||
p 3) |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
e |
pt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3) |
|
|
( p |
1)( p 3) |
|
||||||
p 3 |
|
p 3 |
|||||||||
|
|
|
|
|
|
|
|
||||
= |
1 |
et |
|
|
1 |
e3t |
1 |
e 3t . |
|||
8 |
12 |
24 |
|||||||||
|
|
|
|
|
|
|
|||||
=
Ответ. y 18 et 121 e3t 241 e 3t .
78
Задача 77.
уравнение
Решение.
Решить линейное однородное дифференциальное
y |
|
2 y |
|
y 0 |
с условиями Коши |
|
|
|
y(0) 2, y (0) |
||||
p( pY ( p) y(0)) y (0) 2( pY ( p) y(0)) Y ( p) 0 |
||||||
1
.
p( pY ( p) 2) 1 2( pY ( p) 2) Y ( p) 0 |
|
( p |
2 |
2 p 1)Y ( p) 2 p 1 |
4 0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
( p 2 2 p 1)Y ( p) 2 p 5 |
Y ( p) |
2 p 5 |
|
= |
2 p 5 |
. |
|||
|
|
|
|
|
p 2 2 p 1 |
|
( p 1)2 |
||
Здесь всего один полюс, но он 2-го порядка.
|
(2 p 5)e |
pt |
|
Re s |
|
||
( p 1) |
2 |
|
|
p 1 |
|
||
|
|
||
= (2 p 5)e |
pt |
|
|
|
|||
|
p 1
(причём производная
подразумевается по переменной |
p |
|||||
2e |
pt |
(2 p 5)te |
pt |
|
= 2et 3tet |
|
|
|
|||||
|
|
|
|
|
p 1 |
|
).
.
Ответ.
y 2e |
t |
|
3te |
t |
|
.
Задача 78. Решить линейное неоднородное дифференциальное
|
|
|
5y |
|
4 y e |
3t |
|
|
|
|
|
уравнение |
y |
|
|
|
с условиями Коши |
y(0) 1, y (0) |
|||||
Решение. |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
p( pY ( p) y(0)) y (0) 5( pY ( p) y(0)) 4Y ( p) |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
p |
|
p( pY ( p) 1) 2 5( pY ( p) 1) 4Y ( p) |
1 |
|
|
|
|||||||
|
|
|
|||||||||
p 3 |
|
||||||||||
2
3
.
( p2 5 p 4)Y ( p) p 2 5 |
1 |
|
|
|
|
|
|||
p 3 |
||||
|
|
|||
|
79 |
|
||
( p |
2 |
5 p 4)Y ( p) |
|
1 |
p 3 |
||||||
|
|||||||||||
|
p 3 |
||||||||||
|
|
|
|
|
|
|
|
|
|
||
Y ( p) |
|
1 |
|
|
|
|
|
|
|||
( p 3)( p |
2 |
|
5 p 4) |
( p |
2 |
||||||
|
|
|
|
||||||||
|
|
|
|
|
|
||||||
p3
5 p 4)
. Дальше можно сделать
разными способами: как найти обратное преобразование для каждого слагаемого отдельно, так и объединить их сначала в одну дробь.
|
|
|
|
1 ( p |
3) |
2 |
|
|
|
|
|
|
|
p |
2 |
6 p |
10 |
|||||||||
Y ( p) |
|
|
|
|
|
= |
|
|
||||||||||||||||||
( p 3)( p |
2 |
5 p 4) |
( p 3)( p 1)( p |
|||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Re s |
( p |
2 |
6 p |
|
10)e |
pt |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
= |
|
|
|
|
|
|
|
|
|||||||||||||||
( p 3)( p 1)( p 4) |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
( p |
2 |
6 p |
10)e |
pt |
|
|
|
|
( p |
2 |
|
6 p 10)e |
pt |
|
( |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
( p 1)( p 4) |
|
|
|
|
|
|
( p 3)( p 4) |
|
|
|||||||||||||||||
|
|
|
p |
3 |
|
|
p 1 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(9 18 10)e |
3t |
|
|
(1 |
6 10)e |
t |
|
|
(16 24 10)e |
4t |
||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
|
2( 1) |
|
|
|
|
|
( 2)( 3) |
|
|
|
|
|
|
3 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
. 4)
p |
2 |
6 p 10)e |
|||||
|
|||||||
( p 3)( p 1) |
|||||||
|
= |
1 |
e |
3t |
|
5 |
|
|
|
|
|||||
|
2 |
|
6 |
||||
|
|
|
|
|
|
||
pt
e |
t |
|
|
|
= |
|
|
p 4 |
|
|
|
|
|
2 |
e |
4t |
. |
|
||||
3 |
|
|||
|
|
|
|
|
Ответ.
y(t) |
1 |
e |
3t |
|
|||
2 |
|
||
|
|
|
5 et
6
2 |
e |
4t |
|
||
3 |
|
|
|
|
.
80
