
Дополнительные главы математики
..pdf
|
|
|
|
|
|
|
|
p |
3 |
p |
2 |
2 p 2 |
|
|
|
||||||||
Задача 61. F ( p) |
|
|
|
|
, найти оригинал. |
||||||||||||||||||
p |
3 |
( p |
2 |
|
2 p 2) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Решение. Разложим на простейшие дроби. |
|
||||||||||||||||||||||
p |
3 |
p |
2 |
2 p 2 |
|
A |
|
|
|
B |
|
|
|
C |
|
Dp E |
|
||||||
|
|
|
|
|
|
|
|
|
|
, после приведения к |
|||||||||||||
p |
3 |
( p |
2 |
2 p 2) |
p |
|
p |
2 |
|
p |
3 |
2 |
2 p 2 |
||||||||||
|
|
|
|
|
|
p |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
общему знаменателю, числитель будет иметь вид:
Ap2 ( p2 2 p 2) Bp( p2 2 p 2) C( p2 2 p 2) p3 (Dp E) =
Ap |
4 |
2 Ap |
3 |
2 Ap |
2 |
Bp |
3 |
|
2Bp |
2 |
2Bp Cp |
2 |
2Cp 2C Dp |
4 |
Ep |
3 |
|||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
( A D) p |
4 |
(2 A |
B E) p |
3 |
(2 A 2B C) p |
2 |
(2B |
2C) p 2C . |
|
||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
Приравняем к исходному числителю, где 0 p |
4 |
1p |
3 |
1p |
2 |
2 p 2 . |
|
||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
=
Система уравнений:
|
|
A D 0 |
|
|
2 A B E 1 |
||
|
|||
|
|
||
|
|
2B C 1 |
|
2A |
|||
|
2B 2C 2 |
||
|
|||
|
|
||
|
|
C 2 |
|
|
|
|
|
Из последнего сразу C 1, из предпоследнего B 0 |
, |
из 3-го |
A 0 . |
|||||||||||
Тогда из 1-го D 0 |
, и тогда из 2-го E 1. Итак, |
1 |
|
|
|
1 |
. |
|||||||
|
3 |
|
2 |
|
||||||||||
|
|
|
|
|
|
|
p |
|
|
p |
2 p 2 |
|||
|
|
|
|
|
|
|
|
|
|
|
||||
Далее преобразуем, |
1 |
|
1 |
|
. В 1-м слагаемом можно найти |
|||||||||
|
3 |
|
2 |
|||||||||||
|
p |
|
( p 1) |
1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
вычет в 0:
|
e |
pt |
||
Re s |
|
|
||
p |
3 |
|||
p 0 |
||||
|
||||
=
1 |
e pt |
|
|
|
|
2! |
|
p |
|
p 0 |
|
|
|
=
1t 2e pt 
2p 0
= 12 t 2 .
61
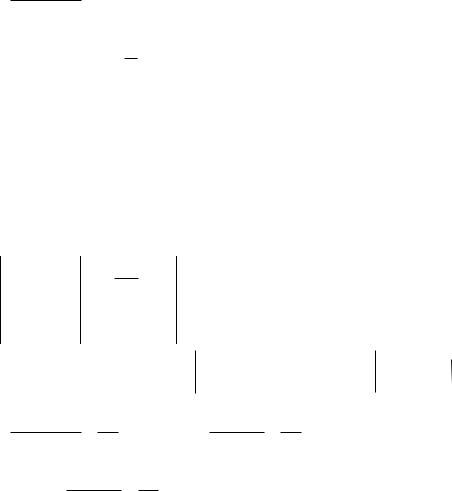
во втором по теореме смещения и известной формуле для синуса,
1 |
|
( p 1) |
2 |
|
Ответ.
Задача
|
|
является преобразованием от |
e |
t |
sin t . |
|||
1 |
|
|||||||
|
|
|
|
|
|
|
||
|
t |
|
t |
2 |
|
|
|
|
e |
sin t |
|
(t) . |
|
|
|
||
|
|
|
|
|
||||
|
2 |
|
|
|
||||
|
|
|
|
|
|
|
||
62. Найти преобразование Лапласа для функции:
2t 3если t (0,1) |
||
f (t) |
0 |
если t (1, ) |
|
||
Решение.
1 |
|
|
(2t 3)e |
pt |
dt |
|
вычисляем «по частям».
0
u 2t 3 |
v |
1 |
e |
pt |
|
|
|||
|
p |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
u 2 |
|
v |
|
e |
pt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2t 3 |
|
|
|
|
|
2 |
1 e pt dt = |
2t 3 |
|
|
2 |
e pt 1 = |
|||||||||||
|
(2t 3)e pt dt |
|
= |
e pt |
|
|
e pt |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
p |
|
|
|
|
|
p |
|
|
|
|
p |
2 |
0 |
||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
0 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5e |
p |
|
3e |
0 |
2 |
|
|
p |
|
|
|
0 |
|
|
3 5e |
p |
2 |
|
|
p |
|
|
|
|
|
||||||||
|
|
(e |
e |
) |
= |
|
(1 e |
) |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
p |
|
|
|
2 |
|
|
|
|
|
p |
|
2 |
|
|
|
|
|
|
|||||||||||||
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
3 5e |
p |
|
|
2 |
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответ. |
|
|
|
|
(1 e |
) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
p |
|
|
|
p |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Задача 63. Найти преобразование Лапласа для функции:
f (t) te2t sin t
62

Решение. Можем воспользоваться набором свойств, доказанных в лекциях, тогда можно даже обойтись без вычисления интегралов.
1) |
Известно, что |
L(sin at) |
|
|
a |
|
, при |
||
p |
2 |
a |
2 |
||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||
2) |
Можно воспользоваться свойством |
L( |
|||||||
a 1 |
: |
|
|
f (t)e |
at |
) |
|
|
|
||
L(sin t)F ( p
a
p ) ,
1 |
. |
||
2 |
1 |
||
|
|||
|
|
||
чтобы
найти
L(sin t)
L(e |
2t |
sin t |
|
|
1 |
||
2 |
1 |
||
p |
|||
|
|||
) .
L(e
2t
sin t) |
1 |
|
|
|
( p 2) |
2 |
1 |
||
|
||||
|
|
=
p |
2 |
|
14 p
.
5
3) Теперь наращивается 3-й множитель: в качестве базовой части
|
2t |
|
|
|
пусть будет L(e |
|
sin t) , вспомним свойство: |
F ( p) L(t f (t)) . |
|
В нашем случае, это означает, что |
|
|
||
L(t f (t)) F ( p) , то есть |
||||
|
|
|
|
|
|
|
|
1 |
|
|
0 (2 p 4) |
|
|
|
|
2 p 4 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2t |
|
|
|
|
|
|
|
= |
|
|
|
|
|
||||||
L(te |
sin t) |
= |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|||
|
p |
2 |
4 p 5 |
( p |
2 |
4 p 5) |
2 |
( p |
2 |
4 p 5) |
2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ. |
|
2 p 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
( p 2 4 p 5)2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Задача 64. Найти преобразование Лапласа для функции:
t f (t) u sin udu
0
.
Решение. |
Здесь функция f (t) - это первообразная от t sin |
||
вычислять её не требуется, ведь существует свойство: |
|||
Если h(t) |
есть первообразная от f (t) , то L(h(t)) |
F ( p) |
. |
|
|||
|
|
p |
|
t
. Но
63

Сначала мы должны узнать преобразование Лапласа от
t sin
t
, а затем
перейти к первообразной, поделив на |
p . |
|
|
|||||||||||
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||||
L(sin t) |
|
|
|
|
|
|
|
= |
|
|||||
|
|
|
|
|
|
|
|
|||||||
|
p |
2 |
1 |
|
|
p |
2 |
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда преобразование от её первообразной: |
1 |
|||||||||||||
p |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 2 p |
||
( p |
2 |
1) |
|
||
2 p |
||
p |
2 |
1 |
|
||
2
=
=
( |
|
( p |
2 |
|
|
|
2 p |
|
|
||
p |
2 |
|
1) |
2 |
|
|
|
||||
2 |
|
|
|
. |
|
1) |
2 |
|
|||
|
|
||||
|
|
|
|
|
|
Ответ. |
|
|
2 |
|
. |
|
|
|
|
( p |
2 |
1) |
2 |
|
|
|
|||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||
Задача 65. Найти обратное преобразование от |
F ( p) |
|
p 6 |
||||||
2 |
8 p 25 |
||||||||
|
|
|
|
|
|
p |
|||
|
|
|
|
|
|
|
|||
Решение.
Способ 1. С помощью свойств и известных функций.
Выделим полный квадрат. |
F ( p) |
|
p 6 |
= |
p 6 |
|
. |
||||||||
2 |
8 p 25 |
( p 4) |
2 |
3 |
2 |
||||||||||
|
|
|
|
|
|
p |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
Если бы в числителе было |
p 4 , то можно было бы использовать |
||||||||||||||
формулу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L(cos at) |
|
|
p |
|
, а учитывая свойство смещения, это значит: |
||||||||||
p |
2 |
a |
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
.
L(e |
4t |
cos at) |
|
p 6
( p 4)2 32
|
p 4 |
|
|||
( p 4) |
2 |
a |
2 |
||
|
|||||
|
|
|
|||
=
p 4
( p 4)2 32
. Разобьём на 2 слагаемых.
|
2 |
. |
|
||
( p 4)2 32 |
Обратное преобразование от 1-го это e 4t cos3t .
64

Во втором,
L(e |
4t |
sin at |
|
если бы в числителе было 3, то как раз было бы
) |
a |
|
|
. Там не 3, но мы домножим и поделим, |
||
( p 4) |
2 |
a |
2 |
|||
|
|
|||||
|
|
|
|
|||
чтобы было. |
|
|
|
|
|
|
|
|
|
|||
Итак, |
|
p 4 |
|
2 |
|
|
3 |
|
|
|
является преобразованием |
|
( p 4)2 32 |
3 ( p 4)2 |
32 |
||||||||||
|
|
|
||||||||||
Лапласа от |
f (t) e |
4t |
cos 3t |
2 |
e |
4t |
sin 3t . |
|||||
|
||||||||||||
|
3 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
Способ 2. С помощью вычетов. Этот способ лучше тем, что не нужно догадываться, к какой форме привести функцию для использования свойств. Просто ищем 2 корня знаменателя, и вычисляем вычеты в этих двух полюсах.
D 64 4 25 36 |
, корни |
p |
8 6i |
4 3i . |
||||
2 |
||||||||
|
|
|
|
|
|
|
||
Re s |
( p 6)e pt |
= Re s |
( p 6)e pt |
|||||
|
|
|
|
= |
||||
|
2 |
|
|
|||||
|
p |
8 p 25 |
|
( p ( 4 3i))( p ( 4 3i)) |
||||
|
|
|
|
|
||||
( p |
6)e |
pt |
|
|
|
|
|
|
|
|
( p 6)e |
pt |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
||||||||||||||
p ( 4 3i) |
|
|
|
|
p ( 4 3i) |
|
|
||||||||||||||||||||
p 4 3i |
p 4 3i |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
(2 3i)e |
4t |
e |
3it |
|
(2 |
3i)e |
4t |
e |
3it |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|||||||||||||
|
|
|
|
6i |
|
|
|
|
|
|
|
|
6i |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2e |
4t |
e |
3it |
|
|
2e |
4t |
e |
3it |
|
3ie |
4t |
e |
3it |
|
3ie |
4t |
e |
3it |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
6i |
|
|
|
|
|
|
6i |
|
|
|
6i |
|
|
|
|
6i |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
=
65
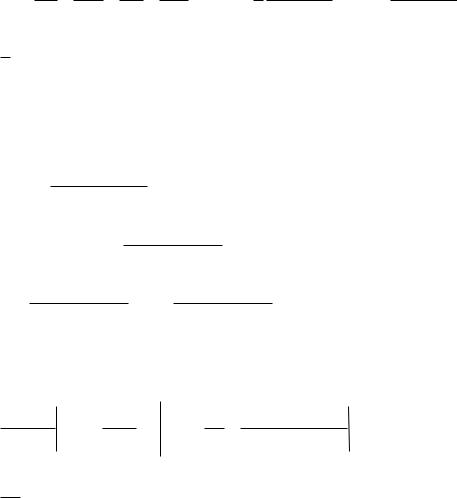
|
|
|
|
e |
|
|
4t |
|
3it |
||
e |
|
||||
|
|
|
|
||
|
|
|
|
|
3i |
|
|
|
|
|
|
2 |
e |
4t |
sin |
||
|
|
||||
3 |
|
|
|||
|
|
|
|
||
Ответ.
|
e |
3it |
e |
3it |
|
e |
3it |
|
|
4t |
2 e |
3it |
e |
3it |
|
|
4t |
e |
3it |
e |
3it |
|
||
|
|
|
|
|
|
|
|
|
|
|
= e |
|
|
|
|
|
e |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
3i |
|
2 |
|
2 |
|
|
|
|
|
2i |
|
|
|
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||||
3t e |
4t |
cos 3t . Получили то же самое. |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
f (t) e 4t |
cos 3t |
2 |
e 4t sin 3t (t) . |
|
|
|
|
|
|
|
|
|
||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 66. Найти обратное преобразование Лапласа от
F ( p) |
1 |
|
. |
|
|
|
||
|
2 |
|
|
|
|
|||
( p 2) |
( p |
3) |
|
|
|
|||
|
|
|
|
|||||
|
Re s |
e |
pt |
|
||||
Решение. |
|
|
= |
|||||
( p 2) |
2 |
( p 3) |
||||||
|
|
|
|
|
||||
|
|
|
|
|
|
|||
=
|
e |
pt |
|
e |
pt |
|||
Re s |
|
|
Re s |
|
|
|||
( p 2) |
2 |
( p 3) |
( p 2) |
2 |
( p 3) |
|||
p 3 |
p 2 |
|||||||
|
|
|||||||
. Полюс p 3 первого
порядка, а |
p 2 |
- 2-го порядка, там нужно сначала найти |
|||||||||||||||||||||||
производную по |
|
p . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
e |
pt |
|
|
|
|
|
|
|
e |
pt |
|
|
|
|
|
e |
3t |
|
te |
pt |
( p 3) e |
pt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
= |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
( p 2) |
2 |
|
|
p |
|
3 |
|
|
|
1 |
|
|
( p 3) |
2 |
|||||||||||
p 3 |
|
|
|
|
p |
|
p 2 |
|
|
|
|
p 2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
3t |
|
|
2te |
2t |
e |
2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
= e3t te2t e2t . |
|
|
|
|
|
||||||||||||||
1 |
|
|
( 1) |
2 |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ.
3t |
2t |
e |
te |
e |
2t |
|
.
66
3.2. Решение дифференциальных уравнений с помощью преобразования Лапласа.
Задача 67. |
Решить |
линейное однородное дифференциальное |
|
уравнение |
|
|
|
x 3x 2x 0 с условиями Коши: x(0) 2 , x (0) 3 . |
|||
Решение. |
|
Раньше, |
во 2 семестре, мы сначала находили сначала |
общее решение, затем частное. Напомним данный метод.
Характеристическое уравнение:
k |
2 |
3k 2 |
0 |
|
(k 1)(k 2) 0 |
, корни 1 и |
|||
|
|||||||||
|
|
|
|
t |
|
|
2t |
|
|
x(t) |
C1e |
|
C2 e |
|
. Далее, при этом x (t) C1e |
||||
тогда из условий Коши получается система:
2, общее решение
t |
2C2e |
2t |
, |
|
|
x(t) C e |
t |
C |
e |
2t |
|
|
|||
1 |
|
2 |
|
|
,
x(0) 2
С С |
2 |
2 |
1 |
|
|
t |
2C2e |
2t |
, |
|
|
|
3 |
|
С1 |
2С2 3 . |
||
x (t) C1e |
|
|
x (0) |
|
|||||||||
Вычитая одно из другого, получим С2 1, |
затем С1 1. |
||||||||||||
Частное решение |
x(t) e |
t |
e |
2t |
. |
|
|
|
|
||||
|
|
|
|
|
|
||||||||
Теперь рассмотрим способ с помощью преобразования Лапласа.
Преобразуем правую и левую часть, зная из теории, как преобразуется производная:
L( f |
|
pF ( p) f (0) . |
|
(t)) |
|
||
L( f |
|
= p pF( p) f (0) f |
|
(t)) |
(0) |
В данном случае, L(x(t)) будет обозначаться X ( p) .
Дифференциальное уравнение превратится в алгебраическое.
L(x 3x 2x) L(0)
67

|
|
|
3( pX ( p) x(0)) |
2 X ( p) = 0 |
|||
p pX ( p) x(0) x (0) |
|||||||
p pX ( p) 2 3 3( pX ( p) 2) 2X ( p) 0 |
|
|
|||||
p |
2 |
3 p 2 X ( p) 2 p |
3 6 0 |
|
|
|
|
|
|
|
|
|
|||
p |
2 |
3 p 2 X ( p) 2 p 3 X ( p) |
|
2 p 3 |
. |
||
|
|
|
|||||
|
2 |
3 p 2 |
|||||
|
|
|
p |
|
|||
|
|
|
|
|
|||
Обратите внимание, что характеристическое уравнение само
получилось слева, как множитель при |
X ( p) . Итак, мы получили |
преобразование Лапласа от искомой функции. А теперь найдём обратное преобразование Лапласа.
X ( p)Re
s (
|
|
2 p 3 |
|
p |
2 |
3 p 2 |
|
|
|||
(2 p 3)e |
pt |
||
|
|||
p 1)( p 2) |
|||
=
=
(
2 p 3 |
, |
|
|
|
|
|
|
|
|
|
|
||
p 1)( p 2) |
|
|
|
|
||
|
|
|
|
|
|
|
(2 p 3)e |
pt |
|
|
(2 p 3)e |
pt |
|
|
|
|
|
|
||
p 2 |
|
|
p 1 |
|
|
|
|
p 1 |
|
|
p 2 |
||
|
|
|
|
|
||
= et e2t .
Причём, условия Коши мы здесь учитываем автоматически, сразу получая частное решение без общего. Умножать на функцию Хевисайда здесь не нужно, т.к. общее решение существует в том числе и на левой полуоси, а оригинал здесь играл лишь вспомогательную роль.
Ответ. x(t) e |
t |
e |
2t |
. |
|
|
|
|
|
|
|
|
|
|
|||
Задача 68. Решить линейное неоднородное дифференциальное |
||||||||
|
|
|
|
3t |
с условиями Коши |
x(0) 0 , |
|
0 . |
уравнение x 3x 2x e |
x (0) |
|||||||
68

Решение. Сначала вспомним метод решения неоднородных уравнений (по виду правой части) из 2 семестра.
Характеристическое уравнение |
k |
2 |
3k 2 |
0 |
, корни 1 и 2, общее |
||
|
|||||||
решение однородного x(t) C1e |
t |
C2 e |
2t |
. |
|
|
|
|
|
|
|
||||
Правая часть b(t) e3t . Но корня 3 нет среди харакреристических, т.е.
не нужно домножать дополнительно ни на какую степенную, а
частное решение неоднородного искать в виде x(t) Ae |
3t |
|
||||||||||||||
|
||||||||||||||||
|
|
3Ae |
3t |
, |
|
|
9 Ae |
3t |
. |
|
|
|
|
|||
x (t) |
|
x (t) |
|
|
|
|
|
|||||||||
Подставляя в дифференциальное уравнение, получим |
|
|
||||||||||||||
|
3t |
|
|
|
3t |
|
|
3t |
|
|
|
3t |
|
1 |
|
|
9Ae |
3 3Ae |
2Ae |
e |
, откуда 2A 1, |
A . |
|
|
|||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
Сумма решений однородного и неоднородного, т.е. общее решение:
x(t) C1e |
t |
C2 e |
2t |
|
1 |
e |
3t |
. Далее надо определить константы из |
||||||||
|
||||||||||||||||
|
|
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
условий Коши. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x(t) C et |
C |
e2t |
|
1 |
e |
3t , |
x(0) 0 |
|
C |
C |
|
1 |
0 |
|||
|
2 |
|||||||||||||||
1 |
|
2 |
|
|
|
2 |
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x (t) C e |
t |
2C |
|
e |
2t |
|
3 |
e |
3t |
|
|
||||||||
|
2 |
|
|
|
|||||
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
,
x (0) 0
C |
2C |
|
|
3 |
0 |
2 |
|
||||
1 |
|
|
2 |
|
|
|
|
|
|
|
Это приводит к системе уравнений, из которой следует |
С2 1 0 |
||||||||
(если из 2-го вычесть 1-е уравнение), С |
|
1 |
С |
1 |
. |
||||
2 |
|
||||||||
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
Итак, ответ: x(t) |
et |
e2t |
e3t |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
2 |
|
|
|
|
|
|
||
69
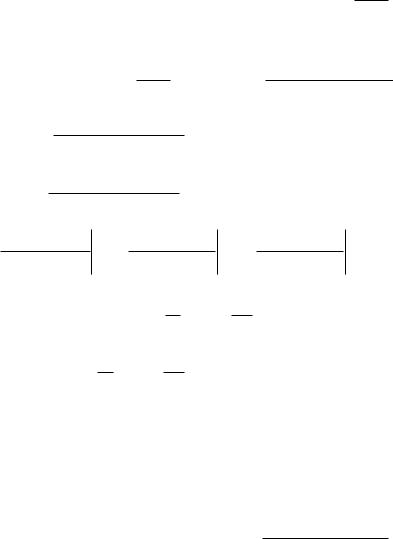
Решим то же самое методом преобразования Лапласа.
p pX ( p) x(0) x
учитывая тот факт,
(0) |
3( pX ( p) x(0)) 2X ( p) |
1 |
|
p 3 |
|||
|
|
что все условия коши здесь нулевые,
, но
получим:
p |
2 |
3 p 2 X ( p) |
1 |
|
|||
|
p 3 |
||
|
|
|
X ( p) |
p |
|
1 |
|
2 |
3 p 2 ( p 3) |
|||
|
||||
|
|
X ( p) |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
. Ищем обратное преобразование: |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
( p 1)( p 2)( p 3) |
|
|
|
|
|
|
||||||||||||||
Re s |
|
|
|
e |
pt |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|||||
|
|
|
|
|
2)( p 3) |
|
|
|
|
|
|||||||||||
|
( p 1)( p |
|
|
|
|
|
|
||||||||||||||
e |
pt |
|
|
|
|
|
|
|
|
|
|
|
e |
pt |
|
|
|
e |
pt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
||||
( p 2)( p 3) |
|
|
|
|
|
|
1)( p 3) |
( p 1)( p 2) |
|||||||||||||
p 1 |
|
( p |
p 2 |
p 3 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
et |
|
|
e2t |
|
|
|
e3t |
|
= |
et |
e2t |
e3t . |
|
|
|
||||||
( 1)( 2) |
|
|
|
|
|
|
|
|
|
|
|||||||||||
1( 1) |
|
|
2 |
|
|
|
2 |
|
2 |
|
|
|
|
||||||||
|
|
|
|
|
e |
t |
|
|
|
|
|
|
e |
3t |
|
|
|
|
|
|
|
Ответ. |
x(t) |
|
|
|
e |
2t |
|
|
. |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2 |
|
|
|
|
2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Задача 69. Решить линейное неоднородное дифференциальное
уравнение |
x 3x 2x e |
t |
с условиями Коши x(0) |
0, x (0) |
0 . |
|
Решение. Как и в прошлой задаче, получается
p2 |
3 p 2 X ( p) |
1 |
|
|
|||
p 1 |
|||
|
|
X ( p) 1
p 2 3 p 2 ( p 1)
70
