
Дополнительные главы математики
..pdf
Заметим, что по теореме смещения, если
L(sin at) |
|
|
a |
|
|
p |
2 |
a |
2 |
||
|
|||||
|
|
|
при
a 7 |
является |
|
7 |
, то домножение на e |
5t |
|||||
|
|
|||||||||
2 |
49 |
|
||||||||
|
|
p |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
F ( p 5) |
, то есть в данном случае |
7 |
|
|
||||||
|
|
|
|
|||||||
( p 5) |
2 |
49 |
||||||||
|
|
|
|
|
|
|||||
полученной функцией.
приведёт к функции
, что и совпадает с
Ответ.
( p
Задача 49.
F ( p) ( p
Решение.
7 |
. |
||
5) |
2 |
||
49 |
|||
|
|||
Найти обратное преобразование Лапласа для
7 |
|
. |
|
|
|
|
|
||
|
2 |
|
|
|
|
|
|
||
5) |
49 |
|
|
|
|
|
|||
|
|
|
|
|
|
||||
F ( p) |
7 |
= |
|
7 |
. Найдём полюсы. |
||||
|
|
|
|
||||||
( p 5) |
2 49 |
p 2 |
10 p 74 |
||||||
|
|
|
|
|
|||||
D 100 4 74 100 296
196
,
p |
10 14i |
|
2 |
||
|
5
7i
.
|
|
|
7e |
pt |
F ( p)e |
pt |
|
|
|
|
|
|||
|
7i))( p (5 7i)) |
|||
|
|
( p (5 |
||
двух особых точках.
, затем найдём сумму вычетов в
51

|
|
7e |
pt |
|
|
|
|
|
|
|
7e |
pt |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
||||
p (5 7i) |
|
|
|
p (5 7i) |
|
|
|
|
|
|
|
|
|
|
||||||||||||
p 5 7i |
|
|
|
p 5 7i |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
7e |
(5 7i)t |
|
|
|
|
|
7e |
(5 7i)t |
|
|
7e |
5t |
e |
7it |
|
7e |
5t |
e |
7it |
||||
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|||||||||
(5 |
7i) |
(5 7i) |
(5 7i) (5 7i) |
14i |
|
14i |
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
5t |
e |
7it |
e |
7it |
|
|
5t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
e |
|
|
|
|
= e |
sin 7t . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
2i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=
Ответ. (t) e5t sin 7t .
Задача 50. Найти преобразование Лапласа
Решение. По свойству линейности, |
L(ch(at |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
at |
|
|
|
at |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
e |
|
e |
|
pt |
|
|
|
|
|
1 |
e |
|
|
|
pt |
|
at |
|
pt |
dt |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
at |
|
e |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
e |
dt |
= |
|
|
|
e |
e |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
||||||||
|
|
|
|
|
(a p)t |
dt |
|
|
(a p)t |
|
|
|
|
|
|
|
|
(a p)t |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
e |
|
e |
dt |
|
= |
|
|
|
|
|
|
e |
|||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
a p |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1 |
|
|
0 1 |
|
|
|
0 1 |
|
= |
1 |
|
|
|
1 |
|
|
|
1 |
|
= |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
a |
|
|
(a p) |
|
|
p a |
p a |
|
|||||||||||||||||||||||||||||
1 |
|
|
|
|
|
2 p |
|
|
= |
|
|
|
p |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
|
p |
2 |
|
a |
2 |
p |
2 |
a |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Ответ. L(ch(at)) = |
|
|
|
|
|
p |
|
|
|
. |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
p 2 a 2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
L(ch(at)) . |
||||
)) |
|
|
at |
|
|
e |
|
||
|
= L |
|
||
|
|
|
|
|
|
|
|
|
|
= |
|
|
||
|
|
1 |
||
0 |
(a |
|||
|
||||
1 |
|
( p a) |
||
|
|
|
|
|
2 |
|
( p a |
||
|
||||
e at |
= |
|
|
|
|
2 |
|
|
|
|
|
e |
(a p)t |
|
|
||
|
|
|
p) |
|
0 |
( p a) |
||
|
|
|
)( p a) |
|
|
|
||
|
= |
|
|
|
|
|
|
=
52
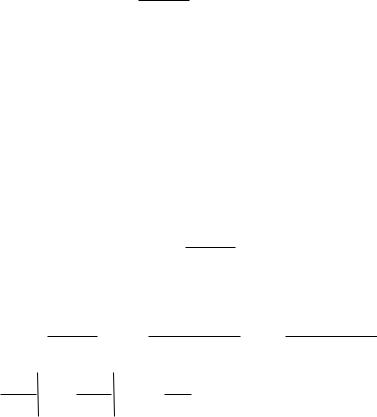
Замечание. Для обычного (не гиперболического) косинуса ранее мы
получали результат
|
|
p |
|
p |
2 |
a |
2 |
|
|
. Для гиперболического - в знаменателе
разность, а не сумма квадратов.
Задача 51.
|
F ( p) |
p |
|
Найти обратное преобразование Лапласа: |
|
. |
|
p2 a2 |
|||
Решение. Чтобы ещё раз повторить метод нахождения обратного преобразования с помощью вычетов , вычислим обратное
преобразование от
F ( p) |
|
|
p |
|
|
p |
2 |
a |
2 |
||
|
|||||
|
|
|
, и убедимся, что при этом
получим |
ch(at) . |
|
|||||||
Re s |
pe |
pt |
|
|
|
|
|||
|
|
|
= Re s |
||||||
2 |
a |
2 |
|
||||||
|
|
p |
|
|
p a |
||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
pe |
pt |
|
|
|
pe |
pt |
|
||
|
|
|
|
|
|||||
p a |
|
p |
a |
|
|||||
p a |
|
|
p a |
||||||
|
|
|
|
|
|
|
|
||
Ответ. ch(at) |
(t) . |
||||||||
|
|
pe |
pt |
|
|
||
|
|
|
|
|
|||
|
|
|
|
|
|
||
( p a)( p a) |
|||||||
|
ae |
at |
|
|
ae |
at |
|
= |
|
|
|
||||
2a |
2a |
||||||
|
|
|
|||||
|
|
|
|
pe |
pt |
|
||
Re s |
|
|
|
|
|
|||
( p a)( p |
||||||||
p a |
||||||||
|
eat |
e at |
|
|||||
= |
|
|
|
|
|
|
= |
|
|
2 |
2 |
|
|
||||
|
|
|
|
|
|
|||
a) ch
=
(at)
.
Аналогично, можно решить задачу для гиперболического синуса.
Меняется лишь знак между двумя слагаемыми.
Задача 52. Найти преобразование Лапласа L(sh(at)) .
53

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
at |
e |
at |
|
|
|
|
e |
at |
e |
at |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pt |
|
|
|
|||||||||
Решение. |
|
L(sh(at)) |
= |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
dt = |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
e |
at |
e |
pt |
e |
at |
e |
pt |
dt |
|
= |
|
|
e |
(a p)t |
dt |
e |
(a p)t |
dt |
|
|
= |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
|
|
1 |
|
|
e |
(a p)t |
|
|
|
|
|
1 |
|
|
|
e |
(a p)t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 |
|
|
p |
|
|
|
|
|
|
|
(a p) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
a |
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
0 1 |
|
0 1 |
|
|
= |
1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
= |
1 |
|
( p a) ( p a) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2 |
|
|
p |
|
|
(a |
p) |
|
|
|
2 |
|
|
|
|
a |
p a |
|
|
|
|
2 |
|
( p a)( p a) |
|
||||||||||||||||||
a |
|
|
|
|
|
p |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
1 |
|
2a |
|
|
|
= |
|
|
a |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
p |
2 |
a |
2 |
|
|
2 |
a |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Ответ. |
L(sh(at)) |
= |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
p |
2 |
|
a |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Задача 53. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Найти обратное преобразование Лапласа от |
F ( p) |
|
a |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||
p2 a2 |
|
||||||||||||||||||||||||||||||||||||||||||
=
Решение.
Re s
ae |
pt |
|
|
|
|
p a |
p |
|
|
|
|
Ответ.
|
ae pt |
|
= Re s |
|||
p |
2 |
a |
2 |
|||
|
|
|
p a |
|||
|
|
|
|
|
|
|
|
|
|
ae |
pt |
|
|
|
|
|
|
|||
|
p |
a |
|
|||
a |
|
|
p a |
|||
|
|
|
|
|
||
sh(at) (t) .
|
|
ae |
pt |
|
|
||
|
|
|
|
|
|||
( p a)( p a) |
|||||||
|
ae |
at |
|
|
ae |
at |
|
= |
|
|
|
||||
2a |
2a |
||||||
|
|
|
|||||
Re s |
|||
|
p a |
||
|
e |
at |
|
= |
|
||
2 |
|||
|
|||
|
|
ae |
pt |
|
|
|
|
( p a)( p |
|||
|
e |
at |
|
|
|
= |
|
|
2 |
||
|
|
|
|
=a)
sh(at) .
54

Задача 54. Найти преобразование Лапласа |
L(t |
2 |
e |
5t |
) . |
|
|
Решение. Наиболее рационально здесь не вычислять интегралы по
определению, а воспользоваться свойствами.
Есть 2 способа.
1)По свойству 4 (теорема смещения)
2)По свойству 7 (дифференцирование изображения).
Способ 1. Зная, что L(t 2 ) |
= |
|
2 |
|
, и свойство L(eat |
f (t)) F( |
|||||||||||||||||||||||||||||
|
p |
3 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
получим |
L(t |
2 |
e |
5t |
) = |
|
|
2 |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
( p |
5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5t |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
||
Способ 2. Зная, что |
L(e |
) |
= |
|
|
|
|
|
|
, и свойство |
F |
|
( p) L(t |
||||||||||||||||||||||
|
|
p |
5 |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
||||||
|
|
2 |
|
|
|
5t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
получим |
L(t |
e |
) = |
|
|
|
|
|
|
|
= |
|
|
|
|
|
= |
|
|
|
|
. |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
( p 5) |
( p |
5) |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Ответ. F ( p) |
|
|
2 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
( p 5)3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Задача 55. Найти обратное преобразование Лапласа для |
|
||||||||||||||||||||||||||||||||||
F ( p) |
2 |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
( p 5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решение. Re s |
|
|
|
2e |
pt |
|
= |
|
1 |
2e pt p |
|
|
|
= t 2e pt |
|
|
= t2e5t . |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
( p |
5) |
3 |
2! |
|
|
|
p 5 |
|
|||||||||||||||||||||||||||
|
p 5 |
|
|
|
|
|
|
|
|
|
|
|
p 5 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ. t2e5t (t) .
p
|
f |
a) ,
(t))
,
55
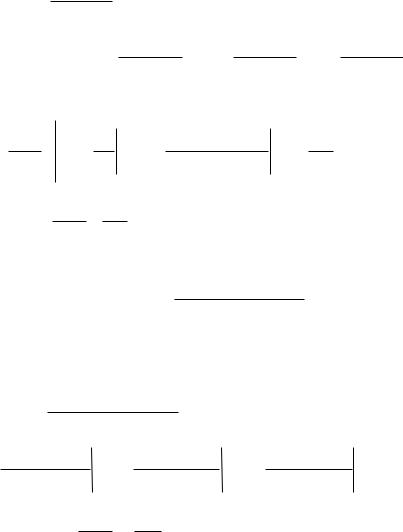
Задача 56. Найти обратное преобразование Лапласа для функции
F ( p) |
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
2 |
( p 3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Re s |
|
|
e |
pt |
|
|
|
e |
pt |
|
|
|
e |
pt |
Решение. |
|
|
|
= Re s |
|
|
|
Re s |
|
|
|
||||||
p |
2 |
( p 3) |
p |
2 |
( p 3) |
p |
2 |
( p 3) |
|||||||||
|
|
|
|
|
p 0 |
|
p 3 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Один из полюсов 2-го порядка, другой 1-го порядка.
|
e |
|
|
|
|
|
e |
|
|
|
|
pt |
|
|
|
|
|
pt |
|||||
|
|
|
|
|
|
|
|
|
2 |
||
|
p |
3 |
|
|
|
|
p |
||||
|
|
|
|
|
|
p |
|||||
|
|
|
p 0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3t 1 |
|
|
e |
3t |
||
Ответ. |
|
|
|||||||||
9 |
|
|
|
9 |
|||||||
|
|
|
|
|
|
|
|
|
|
||
Задача 57. Дано:
|
te |
pt |
( p 3) |
|
= |
|
|||
|
|
( p 3) |
2 |
|
|
|
|
||
3 |
|
|
|
|
|
|
|
|
|
(t) . |
|
|
|
|
F ( p) |
p |
|
( p 1)( p |
||
|
e |
pt |
|
|
||
|
||
|
p 0 |
2)( p 3)
e 3t |
3t 1 |
|
e 3t |
||
= |
|
|
|
. |
|
9 |
|
9 |
|||
9 |
|
|
|
||
. Найти обратное
преобразование Лапласа.
Решение. Способ 1. С помощью суммы вычетов.
Re s |
|
|
|
pe |
pt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= Re s Re s Re s |
= |
|
|
|||||||||||||
( p 1)( p 2)( p 3) |
|
|
|
||||||||||||||||||||
|
|
|
|
p 1 |
|
p 2 |
|
|
p 3 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
pe |
pt |
|
|
|
|
pe |
pt |
|
|
|
|
|
|
|
|
|
pe |
pt |
|
|
|
||
|
|
|
|
+ |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
= |
|||
( p 2)( p 3) |
|
( p 1)( p 3) |
|
|
( p |
1)( p |
2) |
||||||||||||||||
p 1 |
|
p 2 |
|
p 3 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
et |
|
+ |
2e2t |
+ |
3e3t |
= |
1 |
e |
t |
2e |
2t |
|
3 |
e |
3t |
. |
|
|
|
|
|||
|
|
1( 1) |
2 1 |
|
|
|
|
|
|
|
|
|
|
||||||||||
( 1)( 2) |
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||
Способ 2. С помощью разложения на простейшие дроби.
56

p ( p 1)( p 2)( p 3)
знаменателю,
=
A |
|
B |
|
|
p 1 |
p 2 |
|||
|
|
C p 3
, приводим к общему
A( p 2)( p 3) B( p 1)( p 3) C( p 1)( p 2) |
= |
|
|
|
p |
|||||||||
|
|
|
|
( p 1)( p 2)( p 3) |
|
|
( p 1)( p 2)( p 3) |
|||||||
|
|
|
|
|
|
|
||||||||
откуда следует |
|
|
|
|
|
|
|
|
|
|
||||
A( p 2)( p 3) B( p 1)( p 3) C( p 1)( p 2) p |
|
|
||||||||||||
A( p |
2 |
5 p 6) B( p |
2 |
4 p 3) C( p |
2 |
3 p 2) p |
|
|
|
|
||||
|
|
|
|
|
|
|||||||||
( A B C) p |
2 |
( 5A 4B 3C) p (6 A 3B 2C) 0 p |
2 |
1p 0 |
||||||||||
|
|
|||||||||||||
Отсюда получается система линейных уравнений на A, B,C : |
||||||||||||||
|
|
|
|
|
|
|
A B C 0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
5A 4B |
3C 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6A 3B 2C 0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решим её методом Гаусса, преобразую расширенную матрицу.
|
1 |
1 |
1 |
0 |
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
5 |
4 |
3 1 |
|
0 |
1 |
|||
|
6 |
3 |
2 |
0 |
|
|
|
0 |
3 |
|
|
|
|
||||||
Система преобразована к виду:
1 |
0 |
|
|
|
|
|
|
||
1 |
1 |
1 |
0 |
||||||
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
0 |
1 |
2 |
1 |
|
|
4 0 |
|
|
0 |
0 |
2 |
3 |
|
||
|
|
|
|||||||
|
|
|
|
|
|
||||
A B C 0B 2C 1
2C 3
57

Отсюда
С3 2
,
B
2
,
A
1 2
. Тогда обратное преобразование надо
найти для функции |
1 |
|
1 |
2 |
1 |
|
3 |
1 |
. Зная при этом, что |
|
|||||||||||||||||||
2 p 1 |
p 2 |
2 p 3 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
` |
1 |
L(e |
at |
) , с помощью линейности получим |
1 |
e |
t |
2e |
2t |
|
3 |
e |
3t |
. |
|||||||||||||||
|
|
|
|||||||||||||||||||||||||||
p a |
|
2 |
|
|
2 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ. |
1 |
e |
t |
2e |
2t |
|
3 |
e |
3t |
(t) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
||
Задача 58. Дано: |
|
F ( p) |
|
. Найти обратное преобразование |
||||||||||||||||||||||||||
|
p |
4 |
1 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Лапласа. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
p |
2 |
3 |
|
|
|
|
|
p |
2 |
3 |
|
|
p |
2 |
3 |
|||||
Решение. |
|
F ( p) |
|
|
= |
|
|
|
|
|
|
= |
|
|||||||||||||||||
|
|
p |
4 |
1 |
( p |
2 |
1)( p |
2 |
1) |
( p 1)( p 1)( p i)( p i) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Здесь 4 полюса 1-го порядка, |
|
1 |
|
и i . |
|
|
|
|
||||||||||||||||||||||
Re s |
|
|
( p |
2 |
3)e |
pt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
||||||||||||
1)( p 1)( p i)( p i) |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
( p |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
( p2 3)e pt |
|
|
|
|
|
( p2 3)e pt |
|
|
|
|
+ |
|
|
|
|
|
|||||||||||||
|
( p 1)( p2 |
1) |
p 1 |
( p 1)( p2 |
1) |
|
p 1 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
( p |
2 |
3)e |
pt |
|
|
|
|
|
|
( p |
2 |
3)e |
pt |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
||||||||||||
|
( p |
2 |
1)( p i) |
|
|
|
|
2 |
1)( p |
i) |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
( p |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
p i |
|
|
|
|
|
p |
i |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
58
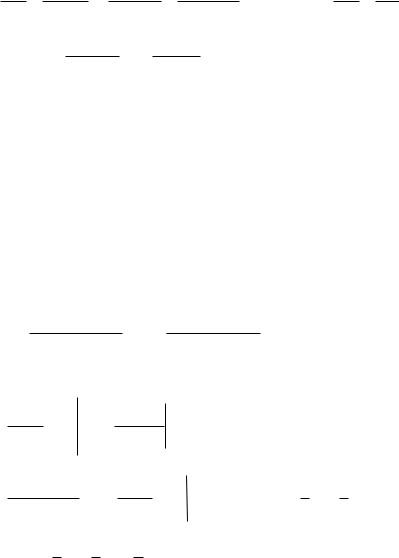
|
t |
|
|
|
4e |
t |
|
2e |
it |
|
|
|
2e |
it |
|
|
|
|
|
e |
it |
|
e |
it |
||
4e |
|
|
|
|
+ |
|
|
|
|
|
= |
t |
e |
t |
+ |
|
|
|
||||||||
2 2 |
( 2) |
|
( 2)(2i) |
|
|
|
e |
|
2i |
|
|
|||||||||||||||
|
|
2 |
|
( 2)( 2i) |
|
|
|
|
|
|
2i |
|||||||||||||||
t |
|
|
t |
|
e |
it |
e |
it |
|
e |
t |
e |
t |
|
|
|
|
|
|
|
|
|
|
|
||
e |
|
|
= |
2 |
|
sin t |
= 2sht sin t . |
|
|
|
|
|||||||||||||||
e |
|
|
|
|
|
2i |
|
|
2 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ. 2sht sin t (t) ..
=
Задача 59. Дано: F ( p) |
p |
. Найти обратное |
|
||
( p 1)2 ( p 2) |
||
преобразование Лапласа. |
|
|
Решение. |
Re s |
pe pt |
|
|
= |
|
||||||
( p 1) |
2 |
( p 2) |
|
|||||||||
|
|
|
|
|
|
|
|
|||||
|
pe |
pt |
|
|
pe |
pt |
|
|||||
Re s |
|
Re s |
|
|
|
|||||||
( p 1) |
2 |
( p 2) |
( p 1) |
2 |
( p |
2) |
||||||
p 1 |
p 2 |
|||||||||||
|
|
|||||||||||
Здесь полюсы 2-го и 1-го порядка, далее.
|
|
|
|
|
|
|
|
|
|
|
pt |
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
pe |
|
|
|
|
|
|
|
|
|||
e |
pt |
|
|
|
|
|
|
|
|
= |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
( p 1) |
2 |
|
|
|
|
|
|
|||||
p 2 |
|
|
|
p 1 |
|
p 2 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
( p 2) p |
|
pt |
|
|
p |
|
|
|
pt |
|
|
|
2e |
2t |
||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
e |
|
|
|
|
te |
|
|
|
|
= |
|||
|
( p 2) |
2 |
|
|
p 2 |
|
|
|
9 |
||||||||||
|
|
|
|
|
|
|
|
|
|
p 1 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ. |
2 |
e |
t |
|
1 |
t |
|
2 |
e |
2t |
(t) . |
|
|
||||||
9 |
|
3 |
te |
9 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
e |
t |
|
1 |
t |
|
2e |
9 |
|
3 |
te |
9 |
|||
|
|
|
|
|
2t
.
59
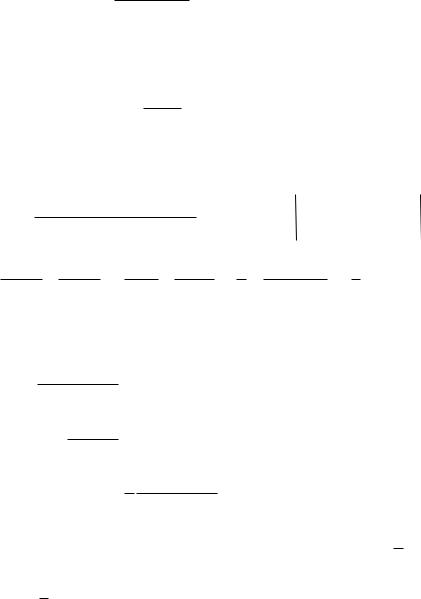
Задача 60. |
F ( p) |
|
1 |
, найти обратное преобразование |
|
2 |
2 p 5 |
||||
|
p |
|
|||
|
|
|
|
Лапласа.
Решение. Способ 1. С помощью вычетов. Найдём корни знаменателя.
D 4 4 |
5 16. |
p |
2 4i |
1 2i . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F ( p) |
|
|
1 |
|
|
= |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
, |
|
тогда |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
p2 |
2 p 5 |
( p (1 2i))( p (1 2i)) |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
e pt |
|
|
|
|
|
|
|
|
|
e pt |
|
|
|
|
|
|
|
|
|
e pt |
|
||||
Re s ( p (1 2i))( p (1 2i)) = |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
p (1 2i) |
p |
|
p (1 2i) |
p 1 2i |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2i |
|
|
|
||||
|
e |
(1 2i)t |
e |
(1 2i)t |
t |
e |
2it |
|
t |
e |
2it |
|
|
1 |
|
|
e |
2it |
e |
2it |
1 |
|
|
|
|||||||
= |
|
|
|
= |
e |
|
|
e |
|
= |
e |
t |
|
= |
|
t |
sin 2t . |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
e |
|
||||||||||
|
|
4i |
|
4i |
|
4i |
|
|
4i |
|
|
2 |
|
|
|
|
2i |
|
|
|
|
|
|
||||||||
Способ 2. Выделить полный квадрат и сгруппировать таким образом:
F ( p) |
1 |
|
|
, затетим, что здесь можно применить формулу |
|||||||
|
2 |
|
2 |
||||||||
( p 1) |
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
L(sin( at)) |
|
|
a |
|
, но не хватает 2 в числителе, поэтому домножим |
||||||
p |
2 |
a |
2 |
||||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||
и поделим. |
F ( p) |
1 |
2 |
|
|
, кроме того, сдвиг на 1 означает, |
|||||
2 |
( p 1) |
2 |
2 |
2 |
|||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||
что в оригинале есть умножение на
e |
t |
|
. Получается в итоге
1 |
e |
t |
sin 2t |
|
|||
2 |
|
||
|
|
|
.
Ответ. 12 et sin 2t (t) .
60
