Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Дополнительные главы математики

..pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

1.98 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 105 6 7 8 9 10 > Следующая >>>

i x

Решение.

i a

sin( a )

2 sin( a ) .

1e i x

=	2	e
=	2
	2

a a

i a

	=
	=

e	i a	1
e		1
2i

Ответ.	2	sin( a )	.

Задача 35. Найти преобразование Фурье от функции:

cos x , x [ , ]
f (x)	0	, x [ , ]

Решение. Здесь мы можем не считать интегралы заново, а

воспользоваться предыдущим примером и свойством

f (x) cos x 12 F ( ) F ( ) .

В качестве базовой части можно считать f (x) 1, и она домножена на cos(1x) , то есть 1. При a , в прошлой задаче ответ бы

выглядел так:

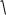
sin( )

. Тогда 12 F ( ) F ( ) =

1	2	sin( ( 1))		sin( ( 1))
					. Далее воспользуемся формулами
			1	1	. Далее воспользуемся формулами
2			1	1

синуса суммы и разности: sin( ) sin( ) cos( ) cos( ) sin( ) .

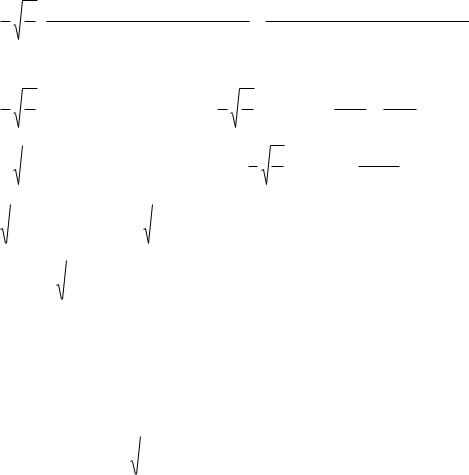
1	2	sin( ) cos( ) cos() sin( )		sin( ) cos( ) cos() sin( )
			1	1
2

учтём, что

sin( )

cos( )

, получится

1	2	sin( )		sin( )
			1	1
2

1	2		1	1
		( sin( ))	1	1
2			1	1

1	2		( 1) ( 1)
		( sin( ))		=
		( sin( ))		=
2			( 1)( 1)
2			( 1)( 1)

1	2	( sin( ))	2
2				2	1

sin( )

sin( ) .

1 2

Ответ.

2 sin( )

1 2

Задача 36. Найти косинус-преобразование Фурье

FС

для функции

1 x , x [0,1]

f (x)

, x [1, )

Решение.

FС ( )

(1 x) cos( x)dx

, здесь нужно

интегрирование по частям.

u 1 x

sin( x)

u 1

v cos( x)

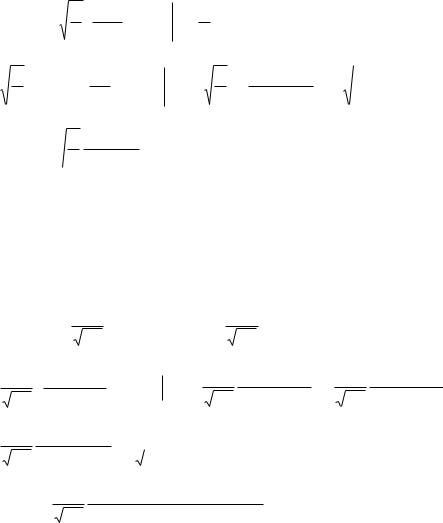
	2	1 x	1
F ( )			sin( x)

С
			0

2			1		1
2	(0	0)	1		cos(x)
	(0	0)			cos(x)
				2
					0

1	1
1	sin( x)dx


	0
	0
	2	cos( )


		2

=	2	1 cos	.

		2

Ответ.

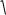
1 cos
	2

Задача 37. Найти преобразование Фурье от функции:

	3x , x [0,2]
e
f (x)	0	, x [0,2]
		, x [0,2]

				1		2											1			2
Решение.						e		3x		e		i x			dx	=				e	(3 i ) x					=
Решение.				2		e				e					dx	=	2			e				dx		=
				2	0												2		0
					0														0
1			1				(3 i ) x						2			1	e	2(3 i )				1			1		1 e	2(3 i )
					e								2		=								=
					e										=								=

2		(3 i)											0			2	(3 i)								2		3 i
2		(3 i)											0			2	(3 i)								2		3 i
1	1 e		6 e 2i				=	1						1 e 6 (cos(2 ) i sin( 2 ))											.
		3 i															3 i
2									2
2									2
			1	1 e			6	(cos(2 ) i sin( 2 ))
Ответ.			1	1 e				(cos(2 ) i sin( 2 ))												.
Ответ.			2								3 i									.
			2								3 i

ГЛАВА 3. Преобразование Лапласа (операционное исчисчление).

3.1. Нахождение оригинала и изображения.

Задача 38.

Найти преобразование Лапласа

L(e

) .

Решение.

F ( p) e

(a p)t

a p

далее обратите внимание на область существования

(a p)t

	0
Re( p)

, иначе

на верхнем пределе получалось бы

e

	1	e
	a p	e
	a p

Ответ.

(a p)t
(a p)t
	0
L(e	at
L(e

)

e		e	0
e		e
	a p
	1	.
		.
p a

0 1 a p

1 p a

Задача 39. Найти обратное преобразование Лапласа для

Решение. Здесь единственный полюс

p a .

F ( p)

1 p a

	Re s	e pt
	Re s	p a
	p a	p a

Ответ. (t

Задача 40.


=	lim e			pt	= e	pt	=	e	at	.
=	lim e				= e		=	e		.
	p a						p a
) e		at	.
) e			.

Найти преобразование Лапласа

t	)
L(te

Решение.

		pt
t		pt
F ( p) te	e		dt
0


=		te	(1 p)t	dt
			(1 p)t

	0

. Далее «по частям»:

u t	v	1	e	(1 p)t
				(1 p)t
		p
	1	p

u 1

v e

(1 p)t

1 p

p 1

0 1

(1 p)t

p 1

1 p

p 1

1 p

( p 1)

Ответ.

L(te

)

( p 1)2

Задача 41. Найти обратное преобразование Лапласа,

F ( p)

( p

Решение. Здесь единственный полюс p 1

, он 2-го порядка.

1
	1)	2
	1)

	e	pt
Re s
	( p 1)		2
p 1

lim e	pt
lim e
p 1


	p

	te	pt
	te	p 1
		p 1

=	t
	te

Производная именно по переменной p ,

p 1	а не t 1. В конце домножаем на
	t	.
Ответ. (t) te

а не t , потому что полюс функцию Хевисайда.

Задача 42. Найти преобразование Лапласа для

1,t (2,3) f (x) 0, t (2,3)

Решение.	F ( p) e pt dt	=	1 e pt	3	=	e 3 p e 2 p	= e 2 p e 3 p .
	3
	2		p	2		p		p
	2

Ответ.

e	2 p	e	3 p
e		e
		p

Задача 43. Найти преобразование Лапласа для

f (x)

0, t (0, a)

1,t (a, )


Решение.		F ( p)			e	pt	dt
						pt

				a
Ответ.	1	e	pa
			pa
	p
	p

1e pt

p a

0e pa

1	e	pa

p

Задача 44. Найти преобразование Лапласа для

f (x)

1,t (0,1)
			(1,3)
t 2,t			(1,3)

	1,t	(1,	)
	1,t	(1,	)

Решение.

F ( p)

( 1)e

(t 2)e

слагаемом интегрирование по частям

u t 2

u 1

v e

, здесь во 2-м

	1			1	t 2			3	1	3			1
				1				3		3
F( p)		e	pt			e	pt			e	pt	dt		e	pt
			pt				pt				pt				pt
	p				p				p				p
	p				p				p				p
				0				1		1						3
				0				1		1						3

3 p

здесь далее взаимоуничтожаются

3 p

F ( p)

e	3 p
e
		p
e	3 p
e
		p
e			3
e
p		2
p

0e 3 p p

e p

, остаётся

Ответ.	1	e p e 3 p	.
	p	p 2

Задача 45. Найти преобразование Лапласа для

	2	, t (0,1)
t		, t (0,1)
f (t)
1, t (1, )

		1
Решение.	F ( p)		t	2	e	pt	dt		e	pt	dt
				2		pt				pt

		0						1

интегрирование по частям в 2 шага.

, здесь в первом слагаемом

u t	2

u 2t

v	1		e	pt

	p

v e		pt

F ( p)

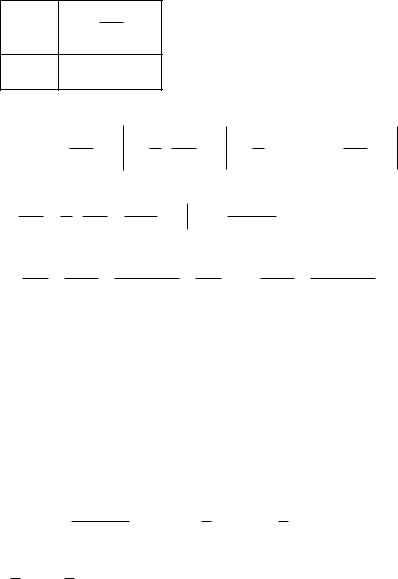
В оставшемся интеграле также «по частям»:

u	2	t
	2
u		1
	2

v				1	e	pt
						pt
	2		p
	2

v		e		pt
v		e
	2

Тогда получаем следующее:

F ( p)

p 2

2(e

Ответ.

2e p

(e p

p 2

1		1		1
		1		e		pt	dt
		p		e			dt
		p
0				0
0 e			p
0 e					=
	p				=
	p
			2e		p			2(
=			2e					2(
=				p	2
					2

			1
			1	e
			p	e

e	p		1)

	p	3

pt

Задача 46.

Решение.

Найти преобразование Лапласа для						f (t) cos	2	t .


F ( p)	cos	2	t e	pt	dt . По формуле понижения степени,

сначала преобразуем квадрат косинуса.

			1		cos 2t				1					1
F ( p)			1		cos 2t	e	pt	dt =	1	e	pt	dt		1	cos 2t e				pt	dt =
							pt				pt								pt
					2				2					2
		0			2				2	0				2	0
		0								0					0
1	L(1)	1		L(cos 2t) , далее можно воспользоваться готовыми
2	L(1)	2		L(cos 2t) , далее можно воспользоваться готовыми
2		2
формулами, выведенными в лекциях:													L(1)			1	,	L(cos at)			p	, в
формулами, выведенными в лекциях:													L(1)				,	L(cos at)			p 2 a 2	, в
																p					p 2 a 2
											48

данном случае												a 2							. Получаем (исходя из линейности
преобразования), что:
							1 1				1					p								1			1					p					1			( p	2		4) p			2
	F ( p)						1 1				1					p					=			1			1					p				=	1			( p			4) p				=
	F ( p)													2							=									2						=							2				=
							2 p				2		p	2					4					2					p	2							2			p( p			2	4)
							2 p				2		p						4					2		p			p			4					2			p( p				4)
1			2 p			2	4						p			2		2
1			2 p				4			=			p					2						.
2		p( p				2	4)			=		p( p					2			4)				.
						2											2


								p	2		2
Ответ.								p			2					.
Ответ.							p( p			2	4)					.
										2

Задача 47. Найти обратное преобразование Фурье для
	F ( p)							p 2 2						.
	F ( p)						p( p		2 4)					.
							p( p		2 4)
Решение.								Re s							( p 2 2)e pt												= Re s									( p 2			2)e pt						нужно
Решение.								Re s													2		4)				= Re s								p( p				2i)( p						нужно
																p( p							4)												p( p				2i)( p				2i)
вычислить по 3 особым точкам: 0,																																2i ,			2i .
Re s								( p 2 2)e pt																=
Re s							p( p		2i)( p											2i)				=
							p( p		2i)( p											2i)
	( p		2			2)e		pt						( p				2		2)e					pt						( p			2	2)e			pt
	( p					2)e								( p						2)e											( p				2)e							=
			p	2	4											p( p 2i)																	p( p 2i)									=
				2
									p 0																		p 2i													p 2i
									p 0																		p 2i													p 2i
	2			( 4 2)e2it											( 4 2)e 2it													=	1				2e2it						2e 2it					=
4						2i(4i)										( 2i)( 4i)												=	2							8				8				=
4						2i(4i)										( 2i)( 4i)													2							8				8
	1			1 e2it				e 2it					=				1				1			cos 2t				=	1 cos 2t								= cos2 t .
	2			2				2					=				2					2		cos 2t				=					2				= cos2 t .
	2			2				2									2					2											2

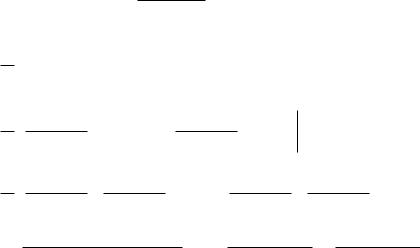
Также домножим на функцию (t) , чтобы обнулить на левой полуоси.

Ответ. f (t) (t) cos		2	t .
Ответ. f (t) (t) cos			t .
Задача 48. Найти преобразование Лапласа для								f (t) e		5t	sin 7t .
Задача 48. Найти преобразование Лапласа для								f (t) e			sin 7t .

Решение. F ( p) e	5t	sin 7t e		pt	dt	=	sin 7t e	(5 p)t	dt , далее можно
Решение. F ( p) e		sin 7t e			dt	=	sin 7t e		dt , далее можно

рассматривать как циклический интеграл, но это нерационально,

лучше представить sin через экспоненты.

7it

sin 7t e

(5 p)t

(5 p 7i)t

5 p

p 7i

0 1

5 p 7i

5 p

p 7i

1 (5 p 7i) (5 p 7i)

14i

(5 p 7i)(5 p 7i)

(5 p)

( p 5)2 49

=
1		=
		=

p 7i
=	7
=		2
(5 p)		2	49
(5 p)			49

<<< < Предыдущая 1 2 3 45 / 105 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.2023650.24 Кб1Дополнительные главы макроэкономики..pdf
#
05.02.2023428.66 Кб3Дополнительные главы математики. Математические модели в экономике-1.pdf
#
05.02.2023371.47 Кб6Дополнительные главы математики. Математические модели в экономике.pdf
#
05.02.2023324.51 Кб1Дополнительные главы математики.-1.pdf
#
05.02.20231.6 Mб0Дополнительные главы математики.-2.pdf
#
05.02.20231.98 Mб1Дополнительные главы математики..pdf
#
05.02.2023827.15 Кб0Дополнительные главы микроэкономики.-1.pdf
#
05.02.20231.1 Mб1Дополнительные главы микроэкономики..pdf
#
05.02.20232.38 Mб8Еnglish for students of Engineering Faculties (basic level)..pdf
#
05.02.2023122.97 Кб3Жанровая организация PR-текста.-1.pdf
#
05.02.2023290.82 Кб2Жанровая организация PR-текста..pdf