
Дополнительные главы математики
..pdf
Но если |
z i |
то |
dz id |
т.е. d |
dz |
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||
i |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
1 |
i |
1 |
|
|
1 |
|
|
1 |
|
|
1 |
e |
zx |
||
Тогда |
|
|
|
|
|
e |
i x |
d = |
|
e |
zx |
dz |
= |
2 |
i Re s |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
2 |
|
1 |
i |
|
2 |
|
|
i |
2 |
i 1 |
z |
||||||||||||||||
|
|
|
|
|
|
i |
1 z |
|
|
|
|
z 1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
e |
zx |
|
|
= e x . Обратите внимание, что это совпало с исходной |
|
|
||||||||||||||||||||
Re s |
|
|
|
|
|
||||||||||||||||||||||
1 z |
|
|
|
||||||||||||||||||||||||
z 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
функцией из задачи 16 в тех точках, где она отлична от 0. |
|
|
|
|
|||||||||||||||||||||||
Ответ. |
e |
x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Более того, даже если бы мы вычислили преобразование Фурье от
0 |
, x A |
при любой граничной точке А, и получили бы |
f (x) |
|
|
e x , x A |
|
|
|
|
|
|
1 |
|
|
1 |
|
e |
(1 i ) x |
|
|
1 |
1 |
(0 e |
(1 i ) A |
) = |
||
|
|
|
|
|
|
= |
|
|
||||||||
i |
2 |
|
i |
2 |
|
|||||||||||
1 |
|
|
A |
1 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
1 |
|
e (1 i ) A , и затем искали обратное преобразование, то |
|||||||||||
|
|
|
|
|
|
|||||||||||
1 i |
|
|
||||||||||||||
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
всё равно получили бы то же самое:
1 |
|
1 |
|
|
|
|
|
1 |
|
i |
1 |
(1 z) A |
|
zx 1 |
|
|
|
|
e (1 i ) Aei x d |
= 2 |
|
1 z e |
|
e |
i dz |
= |
|||||
2 |
1 i |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
i Re s |
1 e (1 z) Ae zx |
= Re s |
e (1 z) Ae zx |
= e x . |
|
||||||||
|
|
|
|
|
|
|
|
||||||||
2 |
i 1 z |
|
1 z |
|
|||||||||||
|
z 1 |
|
z 1 |
|
|
|
|
|
|||||||
=
21
В следующей серии задач мы повторим комплексный ряд Фурье, а также будем находить преобразование Фурье для тех же самых функций, чтобы сравнить.
Задача 18. Представить в виде комплексного ряда Фурье функцию:
f (x) 1
на интервале
( 1,1)
.
Решение. Вспомним формулы:
f
c0
1 n
(x) c |
||||
|
|
|
0 |
|
|
1 |
1 |
|
|
|
dx |
|||
2 |
||||
|
1 |
|||
|
|
|||
e |
in |
e |
||
|
|
|||
|
|
|
2i |
|
|
|
in x |
|
|
|
|
||
cn e |
l |
, где c0 |
||||||
|
|
|||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
= 1. |
cn |
|
|
e |
in x |
dx |
||
|
|
|||||||
|
|
|
||||||
|
2 |
|
|
|||||
|
|
|
|
1 |
|
|
||
|
|
|
|
|
|
|
||
in |
|
1 |
|
|
|
|
|
|
|
= |
|
sin( n ) 0 |
|||||
|
n |
|||||||
|
|
|
|
|
|
|
||
1 |
|
l |
|
|
|
|
f ( |
||
2l |
||||
l |
|
|||
|
|
|
||
= |
|
1 |
||
|
||||
|
|
2in |
||
. Итак,
|
|
|
|
|
1 |
|
l |
|
|
in x |
|
||
x)dx , cn |
|
|
|
|
|
l |
dx . |
||||||
|
|
|
f (x)e |
|
|||||||||
|
|
|
|
|
|||||||||
2l |
|
|
|
|
|||||||||
|
|
|
|
|
l |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
in x |
1 |
|
|
|
|
e |
in |
e |
in |
|
|
|
e |
= |
|
|
|
= |
|||||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
2in |
|
|
|||||||
|
|
1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
cn |
0 |
, ряд состоит лишь из |
|||||||||||
одной константы. Ответ. 1.
Задача 19. Найти преобразование Фурье от функции:
f (x)
1 |
, |
|
, |
0 |
|
|
|
x x
( 1,1)( 1,1)
.
|
|
1 |
|
|
|
Решение. F ( ) |
|
|
f (x)e i x dx = |
||
|
|
|
|||
2 |
|||||
|
|
|
|
||
|
|
|
|
1 |
1 |
|
|
|
e |
i x |
dx |
||
|
||||
2 |
|
|||
1 |
|
|
||
|
|
|
=
|
1 |
|
2 |
||
|
1 |
e |
i x |
1 |
|
|
||
i |
|
1 |
|
|
|
=
1 |
e |
i |
e |
i |
|
|
|||
2 |
|
i |
|
|
=
2 |
e |
i |
e |
|
|||
2 |
|
|
2i |
i
= |
2 |
|
|
||
|
sin
.
В отличие от 18-А, здесь не sin( n ) , а sin( ) |
для произвольного |
действительного числа , и он не равен 0.
Задача 19-Б. Представить эту же функцию интегралом Фурье.
22

Решение. Если мы нашли преобразование Фурье, то нетрудно записать интеграл Фурье следующим образом: подставить найденное
преобразование Фурье в формулу |
f ( |
||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
f (x) |
|
|
F ( )e |
i x |
d |
f (x) |
|||||
|
|
|
|||||||||
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
sin |
|
|
|
|
|
|
|
|
f (x) |
|
e |
i x |
d . |
|
|
|||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
x)
1 
 2
2
1 |
|
|
|
|
|
|
|
|
|
F ( )e |
i x |
d . |
|||||
|
|
|||||||
2 |
|
|
||||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
|
2 sin |
|
|
|
|
|
||
|
e |
i x |
d |
|||||
|
|
|||||||
|
|
|
|
|||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
Замечание. Это интеграл Фурье в комплексной форме. А можно ещё преобразовать экспоненту по формуле Эйлера и свести к интегралу Фурье в действительной форме:
|
1 |
|
sin |
|
|
|
|
f (x) |
|
e |
i x |
d |
|||
|
|
||||||
|
|
|
|||||
|
|
|
|
|
|||
|
|
|
|
|
|
|
1 |
|
sin |
|
|
1 |
|
sin |
|
||
f (x) |
|
cos( x)d i |
|
sin( x)d |
|||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||
Но функция |
sin |
чётна по |
(отношение двух нечётных), тогда |
||||||||
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||
нечётная функция по за счёт sin( x) во 2-м слагаемом, и оно = 0.
А в 1-м чётная, сводится к удвоенному интегралу по полуоси.
|
1 |
|
sin |
|
|
f (x) |
|
cos( x)d |
|||
|
|
||||
|
|
|
|||
|
|
|
|
||
f (x)
2
|
sin |
|
|
||
|
||
0 |
||
|
cos(x)d
.
Задача 20. Представить в виде комплексного ряда Фурье функцию:
23

f (x) x
на интервале
( 1,1)
.
Решение. Найдём коэффициенты. c0 |
|
1 |
|||||||
2 |
|||||||||
|
|
|
|
|
|
|
|
||
|
1 |
1 |
|
|
|
|
|
|
|
cn |
|
xe |
in x |
dx |
нужно интегрирование |
||||
|
|
||||||||
2 |
|
|
|||||||
|
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
2 |
1 |
|
xdx |
= |
1 |
x |
|
|
|
2 |
|
2 |
|
||||
|
|
||||||
|
|
|
|
||||
1 |
|
|
|
1 |
|||
|
|
|
|
|
|||
|
|
|
|
|
|
||
«по частям».
= 0.
u x u 1
v |
|
1 |
e |
in x |
|
|
|||
in |
|
|||
|
|
|
||
v e |
in x |
|
|
|
|
|
|
||
|
|
|
1 |
1 |
|
|
|
|
|
1 |
|
|
x |
|
|
|
1 |
|
|
|
1 |
|
1 |
|
|
|
|
|
|
cn |
|
xe |
in x |
dx |
= |
|
|
e |
in x |
|
|
|
|
e |
in x |
dx |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
2 |
|
2 |
in |
|
|
|
|
in |
|
|
|||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
e |
in |
( 1)e |
in |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
1 |
|
e |
in |
e |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
in x |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
2 e |
|
|
= |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
in |
|
|
i |
2 |
|
2 |
|
|
|
|
|
|
|
|
in |
|||||||||
2 |
|
|
|
|
|
|
|
n |
|
|
|
|
1 |
|
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1-е слагаемое можно преобразовать к cos, 2-е к sin.
=
in |
|
e |
in |
|
e |
in |
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
n |
|
|
|
||
|
|
|
|
|
|
|
||
1 |
ein |
e in |
2 |
|
ein |
e in |
|
|
2i |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
2 |
|
|
||||
2 |
|
2 |
|
in |
|
|
2i |
|
n |
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|||||||
1 |
|
2 |
sin( n ) |
2i |
|
|
|
2 |
cos(n ) |
in |
2 |
|
2 |
|
|
|
n |
|
|||||
|
|
|
|
|
|
||
=
1 |
|
2 |
0 |
|
|
cos(n ) |
in |
|
|
2 |
|
|
|
=
|
i |
|
i( 1)n |
|
i( 1)n |
|
cos(n ) |
|
= |
|
. Тогда ряд: f (x) |
|
ein x . |
n |
n |
n |
||||
|
|
|
|
n |
|
|
|
|
|
|
n 0 |
|
|
24
|
|
i( 1) |
n |
|
|
|
Ответ. |
f (x) |
e |
in x |
. |
||
|
||||||
n |
|
|||||
|
n |
|
|
|
||
|
|
|
|
|
||
|
n 0 |
|
|
|
|
Задача 21. Найти преобразование Фурье от функции:
x , x ( 1,1) |
|
f (x) |
. |
0 , x ( 1,1) |
|
Решение.
|
1 |
|
|
|
|
|
F ( ) |
|
f (x)e |
i x |
dx |
||
|
||||||
2 |
|
|||||
|
|
|
|
|
||
|
|
|
|
|
=
1 |
1 |
|
|
|
xe |
i x |
dx |
||
|
||||
2 |
|
|||
1 |
|
|
||
|
|
|
здесь тоже, как и в прошлом примере, нужно интегрирование по частям, но в конце получится слагаемое с sin , и оно не исчезает, в
отличие от sin( n ) .
u x |
|
|
|
|
v |
1 |
e i x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
u 1 |
|
v e |
i x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
x |
|
|
|
|
|
|
|
1 |
|||||||
|
|
xe i x dx |
= |
|
|
|
|
|
|
|
|
e i x |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
2 |
1 |
|
|
|
|
|
|
|
|
2 |
i |
|
|
|
|
1 |
|
|
i |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
e |
i |
( 1)e |
i |
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
e |
i x |
|
|
|
= |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2 |
|
|
|
i |
|
|
|
|
i |
2 |
|
2 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
|
|
|
ei |
e i |
|
|
ei e i |
|
|
1 |
|
|
e |
||||||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
2 |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
1 |
|
|
|
|
e |
i x |
dx |
|
= |
|
|
|||
1 |
|
|
|
|
1 |
e |
i |
e |
i |
|
e |
i |
e |
i |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
i |
|
|
|
|
|
||||
|
|
|
|
|
|
||||||
i e i |
2 |
|
ei e i |
|
2i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||
2 |
i |
|
2i |
|
|
|
|
|
|
|
|
||||
25
= |
1 |
|
2 |
2 |
|
i |
|
|
|
2i |
cos |
|
2 |
|
|
|
||
Ответ. F (
cos |
2i |
|
= |
1 |
|
|
2 |
sin |
2 |
||
|
|
|
|||
|
|
|
|||
|
sin |
= |
2 |
cos |
|
||||||||
|
|
2 |
|
|
|
i |
|
|
|||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||
) |
|
2 |
cos |
|
sin |
|
|||||||
|
|
i |
|
|
|
|
2 |
. |
|||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2i |
cos |
2i |
|
|
|
|
|
2 |
sin |
|
|
|
|
|||
|
|
|
|
|
|
sin |
|||
|
2 |
. |
|
|
|||
|
|||
=
Задача 21-Б. Представить эту же функцию интегралом Фурье.
Решение. Используя найденное в прошлом пункте преобразование
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
Фурье и формулу |
|
|
f (x) |
|
|
|
|
F ( )e |
i x |
d , получим: |
|||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
2 |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
cos |
|
sin |
|
|
|
|
||||||||||||
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
f (x) |
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
ei x d |
|
||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||||||||
|
2 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
cos |
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
f (x) |
|
|
|
|
i x |
d . |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
2 |
|
e |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
cos |
|
sin |
|
|
|
|
|||||||||||||
|
f (x) |
|
|
|
i x |
d . |
|||||||||||||||||||||
Ответ. |
|
|
|
|
|
|
2 |
|
|
e |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
В лекции было доказано (свойство 5): если для непрерывной |
|||||||||||||||||||||||||||
функции |
lim |
f (x) 0 |
то |
Ф f |
|
|
|
|
|
||||||||||||||||||
|
(x) i F( ) . Но если функция |
||||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
задана только на конечном интервале, то слагаемое, которое исчезало в 0 в том случае, не исчезает.
26
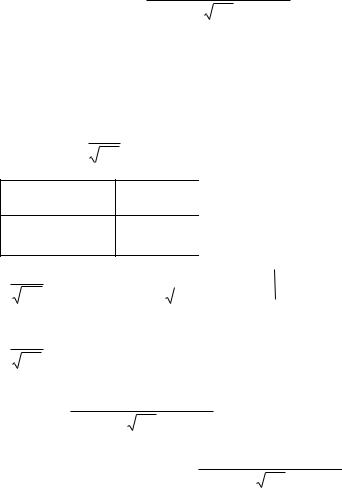
Задача 22. Доказать формулу:
Ф f (x) i F ( ) |
f (b)e |
i b |
f (a)e |
i a |
|||
|
|
|
|||||
|
|
|
|
2 |
|
||
|
|
|
|
|
|
|
|
для функции: |
|
f (x) , x (a,b) |
|||||
f (x) |
0 |
, x (a,b) |
|||||
|
|
|
|||||
Решение.
Ф f |
|
1 |
|
||
(x) = |
2 |
|
|
|
u e i x
u i e i x
b |
|
|
|
i x |
|
|
|
f |
|
|
dx . Интегрирование по частям: |
||
|
|
|
||||
|
(x)e |
|
|
|||
a |
|
|
|
|
|
|
v |
|
|
||||
f (x) |
|
|
||||
v |
f (x) |
|
|
|||
|
|
|
|
|
|
|
1 |
b |
|
i x |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
(x)e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
dx = |
|
|
|
|
|
f (x)e |
||||
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|||
a |
|
|
|
|
|
|
|
|
|
|||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( f (b)e |
i b |
f (a)e |
i a |
) i |
|
||||||||
2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
f (b)e |
i b |
f (a)e |
i a |
|
||||||||
F ( ) |
|
|
|
|
|
|
. |
|
||||||
|
|
|
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
f (b)e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ. Ф f (x) i F ( ) |
|
|
|
|||||||||||
i x b |
|
b |
|
i f ( |
|||
a |
|||
|
a |
||
|
|
||
|
i x |
|
|
f (x)e |
dx |
||
|
|||
|
|
|
|
|
|
|
|
i b |
f (a)e |
i a |
|
|
|
|
2 |
|
|
|
|
x)e |
i x dx |
= |
|
|
|
|
|
|
= |
|
|
Существует понятие свёртки функций, определяемое следующим
образом: f g f ( )g(x )d .
27

Задача 23. Доказать, что если рассматривать преобразование Фурье
свёртки без коэффициента
1 
 2
2
(обозначим
Ф |
, F |
1 |
1 |
соответственно),
то оно равно произведению аналогичных преобразований двух исходных функций: Ф1 f g F1 ( )G1 ( ) .
Решение.
|
|
|
|
|
f |
|
|
|
|
|
|
( )g(x )d
|
i x |
|
|
e |
dx |
||
|
|||
|
|
|
|
|
|
|
. Это двойной интеграл. Мы
можем изменить порядок интегрирования. Причём здесь не надо пересчитывать границы, ведь оба интеграла по всей оси.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i x |
|
|
|
|
|
|
|
|
i x |
|
|
|
|
|
|
f ( )g(x )e |
|
dx |
|
d |
= |
|
g(x )e |
|
|
dx |
|
d . |
|||||
|
|
|
|
|
f ( ) |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Вынесли f ( ) |
во внешний интеграл, как величину, не зависящую от |
|||||||||||||||||
переменной x . |
Здесь во внутреннем интеграле можно применить |
|||||||||||||||||
свойство 3 - сдвиг по аргументу: |
Ф1 g(x a) e |
i a |
G1 |
( ) . |
||||||||||||||
|
|
|||||||||||||||||
|
f ( ) e |
|
G1 ( ) d |
|
|
|
|
|
|
i |
= G1 ( ) |
|
f ( )e |
i |
d |
||
|
|
|||||||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
= G1 ( )F1 ( )
.
Замечание.
Ф f
g |
2 F ( )G( ) |
, если рассматривать исходное
определение с коэффициентом
1 
 2
2
.
28
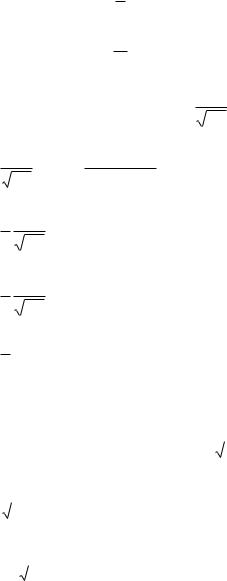
Задача 24. Доказать свойства:
[ f (x) cos x] |
1 |
[F ( ) F ( )] |
|
|
|
|
|
|
|
||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
[ f (x) sin x] |
1 |
[F ( ) F ( )] |
|
|
|
|
|
|
|
||||||||||||||||||||||
2i |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
[ f (x) cos x] = |
|
|
f (x) cos( x)e |
i x |
dx |
|||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
|
2 |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
|
|
e |
i x |
|
e |
i x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
f (x) |
|
|
|
e |
i x |
dx = |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x)e |
i x |
e |
i x |
dx |
|
|
f (x)e |
i x |
e |
i x |
dx |
|
= |
|
|
||||||||||
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
f (x)e |
i( ) x |
dx |
|
|
f (x)e |
i( ) x |
dx |
|
= |
|
|
||||||||||||||
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
[F ( ) F ( )] . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=
Аналогично,
[ f (x) sin x]
|
|
1 |
|
|
|
= |
|
|
f (x) sin( x)e i x dx = |
||
|
|
|
|||
2 |
|||||
|
|
|
|
||
|
|
|
|
1 |
|
|
|
|
|
ei x |
e i x |
|
|
|
|
|
|
|
|||||||
|
|
|
f (x) |
e i x dx = |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
2i |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
f (x)e |
i x |
|
i x |
dx |
f (x)e |
i x |
|
i x |
|
|
||
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
e |
|
dx |
= |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2i |
2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
29
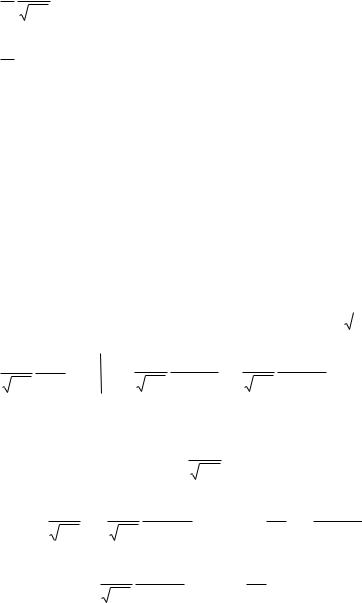
1 |
1 |
|
|
|
|
|
|
|
|
f |
|
2i |
2 |
|
|
||
|
|
||||
|
|
|
|||
1 |
[F ( ) |
||||
2i |
|||||
|
|
|
|
||
Задача 25.
(x)e |
i( ) x |
dx |
|
||
F ( )]. |
||
Дана функция
f
f (x)e |
i( |
|
1 |
, x |
(x) |
, x |
0 |
|
|
|
|
|
|
|
) x |
dx |
|
= |
|
|
||
|
|
|
|
|
|
|
|
(0,1) |
. |
|
(0,1) |
||
|
1)Найти её преобразование Фурье
2)Представить эту функцию в виде интеграла Фурье.
Решение. Найдём преобразование Фурье.
1 |
1 |
|
|
1 |
1 |
e |
i |
1 |
|
i |
e |
|
i x |
|
|
||||||||
e |
= |
|
= |
||||||||
|
|
|
|
|
|
|
|
||||
2 |
i |
|
2 |
|
i |
2 |
|
||||
|
|
0 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Представим в виде интеграла Фурье.
|
|
|
1 |
1 |
||
F () = |
|
|
e i x dx = |
|||
|
|
|
||||
2 |
||||||
|
|
|
0 |
|||
|
|
|
|
|||
i |
1 |
|
|
|
||
|
|
|
|
|||
|
|
|
|
|
|
|
Используя формулу
|
1 |
|
|
i |
|
|
|||
f (x) |
|
|
|
|
2 |
|
2 |
||
|
|
|
||
Ответ. |
F () = |
|
i |
|
|
2 |
|||
|
|
|
|
|
e
f (x) |
|
|
1 |
||||
|
|
2 |
|||||
|
|
|
|
|
|
||
e |
i |
1 |
|
|
i x |
||
|
|
|
|
|
e |
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
i |
1 |
|
|
|
|
||
|
|
, |
|
f (x |
|||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
F ( |
|
|
|
d = |
|
) |
i |
|
2 |
)e |
i x |
d , получим: |
|
||||||||||
|
|
|
|
||||||||||
i |
|
|
e |
i |
1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
i x |
d |
|
|
|
|
|
|
|
|
|
|
|||||
2 |
|
|
|
|
|
e |
|
||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||
|
e i |
1 |
|
|
|
|
|
|
|||||
|
i x |
|
|
|
|||||||||
|
|
|
|
|
|
|
d . |
||||||
|
|
|
|
|
e |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
.
30
