Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Дополнительные главы математики

..pdf

Скачиваний:

Добавлен:

05.02.2023

Размер:

1.98 Mб

Скачать

☆

1 / 101 2 3 4 5 6 7 8 9 10 > Следующая >>>

Томский государственный университет систем управления и радиоэлектроники

Приходовский М.А.

Дополнительные главы математики Курс практических занятий (Семестр 4)

Учебное пособие

для специальности 09.03.01

Томск

ТУСУР

2019

Электронное учебное пособие составлено по материалам практических занятий, проведённых на ФСУ в группах 437-1,2,3 весной 2019 года.

Охвачены следующие темы. Интегралы, зависящие от параметра. Интеграл и преобразование Фурье. Преобразование Лапласа.

Оглавление по темам
ГЛАВА 1. Интегралы, зависящие от параметра ..................................	4
1.1. Вычисление интегралов, зависящих от параметра......................	4
1.2. Формула Лейбница и её применение..........................................	14
ГЛАВА 2. Интеграл Фурье и преобразование Фурье.......................	19
2.1. Вычисление интеграла Фурье и преобразования Фурье............	19
2.2. Синус-преобразование и косинус-преобразование Фурье.........	32
ГЛАВА 3. Преобразование Лапласа (операционное исчисление)....	44
3.1. Нахождение оригинала и изображения.........................................	44
3.2. Решение дифференциальных уравнений с помощью
преобразования Лапласа.........................................................................	67
3.2. Решение интегральных уравнений с помощью преобразования
Лапласа......................................................................................................	83

ГЛАВА 1. Интегралы, зависящие от параметра

1.1. Вычисление интегралов, зависящих от параметра

Задача 1. Вычислить А).

Решение.

I ( y)

1
xy	2	dx
xy		dx
0

. Б)

I ( y)

xy2 dx

		1						x	2			1
		1

А). I ( y)				xy	2	dx	=			y	2		, формула Ньютона-Лейбница



		0						2				0
		0

применяется здесь по переменной																			x , получим						1	y	2	0 =
																											2
																									2
																									2
y		2										y	2
y								x2								( y 2 )2							y 2	y 2 = y 6 y 4
Б) I ( y)				xy2 dx			=	x2		y 2				=		( y 2 )2						y 2	y 2
Б) I ( y)				xy2 dx			=			y 2				=								y 2
								2									2					2						2
	y							2				y					2					2						2
												y
Ответ. А)			y 2		. Б)			y 6		y 4			.
Ответ. А)				2	. Б)					2			.
				2						2
														1			2			2
																	2			2
Задача 2.		Вычислить								I ( y)					xe		x	y			dx .
																	x	y

y	2

2

Решение. В данном случае вовсе не требуется интегрирование по

частям, ведь в степени экспоненты 2-я степень от					x , а другом
множителе есть 1-я степень можно подвести под знак
дифференциала.
1	1	1	1	1		1	1
I ( y) xex2 y2 dx =		e x2 y2 2xdx =		e y2 x2 d (x 2 )	=		e y2t dt
	2		2			2
0		0		0			0

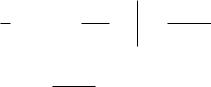
Обратите внимание, что при замене t x	2

меняется, хотя для какого-нибудь другого изменились.

интервал (0,1) не интервала границы бы

1	1							1					1
	1	2										2
	e	2	t									2	t
		y	t	dt	=						e	y	t
2				dt	=		2 y			2	e
2	0												0



				e	y	2	1
					y
Ответ.									.
Ответ.					2 y		2		.
							2

Задача 3. Вычислить

e	y	2


	2 y		2

x	y	ln	3

1	.

xdx

Решение. Интегрирование по частям здесь не упрощает интеграл. Но может помочь дифференцирование или интегрирование по параметру.

Заметим, что (x

) y

ln x (производная по y здесь считается, как

от показательной, а не степенной функции). Тогда (x

) yy

x ,

(x y )

x y ln 3

x . Таким образом, внутри того интеграла, который

yyy

нам надо найти, 3-я производная по параметру от x y . Тогда то, что

нам надо найти, можно обозначить так:

1		ln
I ( y) x	y	ln	3
	y		3
0

xdx

. Можно

воспользоваться формулой Лейбница для случая постоянных границ и

сначала найти I ( y) x y dx , а затем полученный результат

продифференцировать 3 раза по y .

I ( y

т.е.

	1					x	y 1	1		1
							y 1

)		x	y	dx	=				=
			y
						y	1			y 1
	0					y	1	0		y 1
	0

действия как со степенной,

здесь интегрируется по переменной

а не показательной функцией.

I ( y)	1	I ( y)	1		I ( y)	2
	y 1
			( y 1)	2		( y 1)	3

I ( y)

Ответ.

Задача

6		.
( y 1)	4	.
	4

6		.
( y 1)	4	.
	4

4. Вычислить

1	y	b	y	a
				dy
		ln y
0

при

b a

Решение. Воспользуемся переходом к двойному интегралу и сменой порядка интегрирования в нём. Заметим, что выражение внутри интеграла напоминает результат применения формулы Ньютона-

Лейбница в границах от a до b . Его можно переписать в виде:

ln y

Теперь надо установить, первообразная от какой функции там

присутствует. Заметим, что

( y x )

y x

ln y

(производная по

данном случае, как

от показательной функции).

А первообразная

тогда имеет вид

. Значит,

= y

dx dy .

ln y

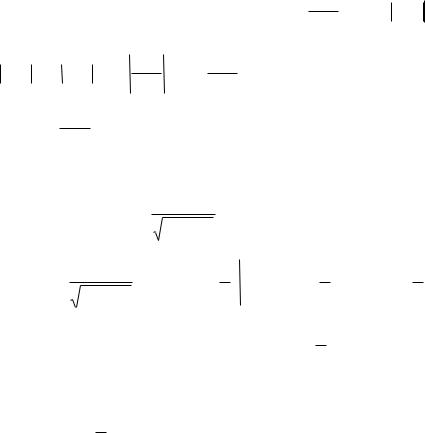
Теперь получили двойной интеграл по прямоугольной области.

Сменим порядок интегрирования, чтобы во внутреннем интеграле было действие по переменной y . Это удобнее в данном случае тем,

что в таком случае сначала действие происходит с данной функцией как со степенной, а не показательной.

1 b

b 1

dx dy =

0 a

a 0

x 1

ln b 1 ln a 1 = ln

b 1

a 1

= ln

a 1

b 1

Ответ. ln

a 1

Задача 5. Вычислить

dx .

		b	1
dx	=		1
dx	=		x 1
			x 1
		a
		a

(учитывая b

	= ln x 1	b
	= ln x 1	a
		a
	0).

Решение.

1			1
				dx
		2
1	y		x	2

= arcsin

x


	y

= arcsin

	1
		arcsin

y

1 y

  

, что

из-за нечётности арксинуса приводит к

2arcsin

1 y

  

Область определения этой функции: y ( , 1] [1, ) .

Ответ.

2arcsin

1 y

  

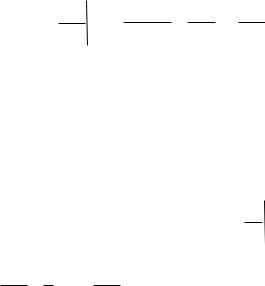
Задача 6. Вычислить

I ( y)

xydx

. Вычислить производную

I ( y)

двумя способами: без формулы Лейбница и по формуле Лейбница.

			2 y				x	2	y	2 y		(2 y)	2	y	y	2	y		3 y	3
			2 y

Решение.		I ( y)		xydx =							=							=		.
								2				2				2			2

			y							y
			y							y
	3y3		9 y		2
I ( y)						.
I ( y)						.
		2	2
		2	2

b( y)

I ( y)

f (x, y)dx b ( y) f (b( y), y) a ( y) f (a( y), y)

a( y)

2 y

(xy) y dx 2 (2 y) y 1 y y

xdx 4 y

4 y 2 y 2

3y 2

9 y

. Результаты совпадают.

Замечание. Во многих случаях можно обойтись без формулы Лейбница, однако она всё же бывает очень необходима в тех случаях,

когда сам исходный интеграл чрезвычайно сложный, а интеграл с производной по параметру оказывается проще.

Ответ.	I ( y)	3y3	,	I ( y)	9 y 2		.
Ответ.	I ( y)		,	I ( y)			.
		2			2
									1
Задача 7. Вычислить I ( y)									1		dx .

						x		2	y	2
						x			y

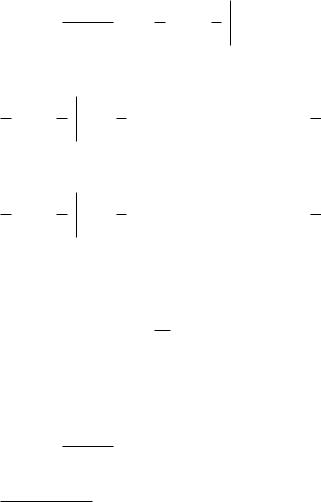
Решение. Способ 1. Без вычетов.

I ( y)

При

				1
				1		dx
	x		2	y	2	dx
	x			y

0		:

1
	arctg
y
y

1	x
	arctg
y
	y

При y 0 :

=	1	arctg( ) arctg( )
	y

1

	2
y	2	2

1	x
	arctg
y
	y

=	1	arctg( ) arctg( )
	y

1

y	2	2

При y 0

четверти,а

значения тоже больше нуля, то есть график в 1-й и 2-й

не в 1-й и 3-й как гипербола. Можно записать эту функцию

таким образом:

I ( y)

Способ 2. С помощью вычетов.

				1
I ( y)				1			dx
I ( y)		x	2	y		2	dx
		x		y

	1				. При
(z iy)(z iy)					. При
(z iy)(z iy)

полуплоскости, это


	1
. Рассмотрим функцию f (z)			=
		z 2 y 2
y 0	один полюс 1-го порядка в верхней
z iy	. При y 0 наоборот, z iy .

При y 0 :

		1			1
I ( y)				dx = 2 i Re s		=

	2	y	2		(z iy)(z iy)
x				z iy

2 i	1	=	2
	z iy
		z iy

Аналогично, При			y

1	=		.
2iy		y

получилось бы

Ответ.

I ( y)

Задача 8. Вычислить

I ( y)



ye	yx	dx

Решение. Здесь не нужно интегрирование по частям, так как зависимость от x только в одном, а не в двух множителях.

					1


I ( y)		ye yx dx =					= e

				y	y	e yx
	0				y		0
							0
Но это получается только при							y 0 .
было бы e			. Область сходимости y
было бы e			. Область сходимости y

yx		= (e	e

	0

В другом случае,

(0, ) .


0	)	= (0 1)		=1.

вместо e			там

Ответ.

I ( y)

, существует при

Задача 9. Вычислить I ( y) xe yx dx .

Решение. В отличие от прошлой задачи, здесь нужно интегрирование

по частям.

1 / 101 2 3 4 5 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.02.2023650.24 Кб1Дополнительные главы макроэкономики..pdf
#
05.02.2023428.66 Кб4Дополнительные главы математики. Математические модели в экономике-1.pdf
#
05.02.2023371.47 Кб7Дополнительные главы математики. Математические модели в экономике.pdf
#
05.02.2023324.51 Кб1Дополнительные главы математики.-1.pdf
#
05.02.20231.6 Mб1Дополнительные главы математики.-2.pdf
#
05.02.20231.98 Mб2Дополнительные главы математики..pdf
#
05.02.2023827.15 Кб0Дополнительные главы микроэкономики.-1.pdf
#
05.02.20231.1 Mб2Дополнительные главы микроэкономики..pdf
#
05.02.20232.38 Mб8Еnglish for students of Engineering Faculties (basic level)..pdf
#
05.02.2023122.97 Кб3Жанровая организация PR-текста.-1.pdf
#
05.02.2023290.82 Кб2Жанровая организация PR-текста..pdf