составляющих реакций противоположны направлениям, выбранным нами.

Не нужно вносить изменения в чертеж или ответ: знаки в ответе получились в соответствии с выбранными и показанными на схеме направлениями, и при анализе полученных результатов это сразу понятно.

4. Проверяется решение. В большинстве задачников ответ обычно приводится. Когда ответа нет, можно рекомендовать для проверки несколько вариантов.

4.1 Проверяется размерность получаемых величин. Не всегда совпадение размерности означает правильность решения, но несовпадение означает точно наличие ошибки.

4.2 Рассматриваются т.н. асимптотические случаи, когда в задаче можно предположить, что заданные величины могут приобретать некоторые «крайние» значения (углы в 0 или 90 градусов, силы стремятся к нулю или бесконечности и т.д.), причем для этих вариантов решение становится тривиальным (очевидным). Если для таких случаев полученное решение не пригодно, скорее всего, оно ошибочно.

1.2. Плоская система сил

Система сил называется плоской, если линии их действия лежат в одной плоскости. В этом случае все силы – активные и реакции связей – действуют в этой плоскости, и при составлении уравнений равновесия следует вводить и использовать двумерную систему координат. В общем случае равновесие тела требует выполнения шести уравнений в

проекциях (три проекции главного вектора и три проекции главного момента на оси системы координат должны быть равны нулю). В плоском случае остается два уравнения в проекциях главного вектора и одно уравнение для главного момента, т.е. три уравнения (так называемая основная форма условий равновесия).

Рассмотрим примеры решения задач.

Пример 1.1

На гладкой горизонтальной поверхности стоит цилиндр весом Р, вертикально вниз на него действует сила Q, линия действия которой направлена по оси. Найти давление N цилиндра на плоскость.

Решение

В этой задача цилиндр находится в равновесии потому, что сила тяжести Р и дополнительная сила Q уравновешиваются реакцией опоры N. Когда в условии говорится «гладкая» поверхность, это означает, что нет сил трения, а реакция опоры может быть направлена только по нормали к ней, в данном случае вверх. Выбирая для вертикальной оси направление вверх за положительное, получим

8

N – P – Q = 0, или N = P + Q.

Пример 1.2.

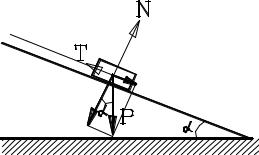
На гладкой наклонной поверхности, образующей угол α с горизонтальной поверхностью, груз Р удерживается нитью, параллельной наклонной поверхности. Найти давление груза на поверхность и натяжение нити.

Решение

В этом примере на груз действуют сила тяжести и две реакции – нити и реакция опоры. Направления этих реакций определяются сразу: для гладкой поверхности, как и в предыдущем примере, реакция опоры направлена по нормали к ней, а реакция нити может быть направлена только вдоль нити в сторону ее закрепления.

Сила тяжести может быть разложена на две взаимно перпендикулярные составляющие, в данном случае по нормали к поверхности и вдоль нее. Тогда реакция плоскости равна нормальной составляющей, а натяжение нити – касательной, причем в силу ортогональности этих направлений проекции реакций не влияют друг на друга. Итак:

T = P sinα, N = P cosα.

Разложение сил по заданным направлениям

В рассмотренном примере 2 сила тяжести относительно просто представляется ее составляющими вдоль двух ортогональных направлений. Однако очень часто встречаются ситуации, когда разложение необходимо сделать вдоль двух произвольных направлений. По существу это означает, что по известной диагонали параллелограмма и заданным направлениям его сторон нужно построить сам параллелограмм. Такого рода разложения необходимо строить в задачах, когда, например, ищутся напряжения в двух стержнях или нитях, на которых подвешен груз.

9

На рисунке приведены примеры разложения вектора P вдоль двух произвольных (непараллельных) направлений на составляющие S1 и S2.

Пример 1.3.

Груз Р висит на двух тросах, образующих с горизонталью углы α и β. Найти натяжения тросов.

Решение

Разложим вектор силы тяжести Р на составляющие, направленные вдоль тросов – величины S1 и S2.

Рассмотрим два способа решения такого типа задач.

1 способ.

Величины Р, S1, S2 образуют систему сходящихся сил – они все проходят через точку В. Для равновесия системы необходимо, чтобы силовой многоугольник был замкнут, т.е. из векторов Р, S1, S2 можно построить треугольник BDE. Но из теоремы синусов для этого треугольника следует

10

Отсюда

2 способ.

Проектируем силы на горизонтальную и вертикальную оси, и суммируем соответствующие проекции, причем при равновесии эти суммы равны нулю. Получаем

S2 cosα − S1 cosβ = 0, S2 sin α + S1 sinβ = P.

Решение этой системы дает тот же результат, что и ранее.

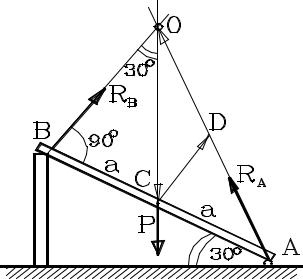
Пример 1.4.

Однородная балка весом Р наклонена к горизонту под углом 30о и опирается правым концом на шарнир, а левый конец балки лежит на выступе стены, причем трением можно пренебречь. Найти реакции шарнира и выступа стены.

Решение

В этом примере известны направления и линии действия двух сил: сила тяжести балки проходит через ее середину вертикально, а реакция выступа стены действует по нормали к балке, так как трением пренебрегаем. По

теореме о трех силах линия действия третьей силы– реакции шарнира – должна проходить через ту же точку О, где пересекаются линии действия двух известных сил. В силу равновесия системы силовой треугольник должен быть замкнут. Направления же всех сил известны, поэ тому силовой

11

треугольник подобен геометрическому треугольнику CDO. Из этого подобия следует

OCP = CDRB = ODRA ,

и для решения необходимо найти соотношения между сторонами в треугольнике OCD. Линия CD – средняя для треугольника AOB.

Обозначим длину балки AB = 2a. Тогда

OC = BC/sin30o = 2a, CD = OB/2 = a√3/2,

DO = AD = ((AB2 + OB2)1/2)/2 = a√7/2.

После определения всех сторон можно найти величины реакций RB,

RA:

RA = P ODOC = 0,66P, RB = P OCCD = 0,43P.

Пример 1.5.

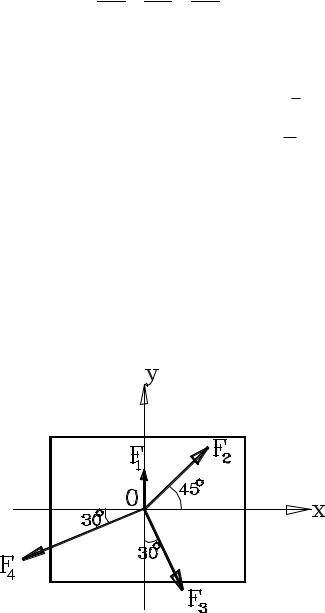
В точке О твердого тела приложены четыре силы, направления которых указаны на рисунке, при этом величины сил: F1 = 2 H, F2 = F3 = 4 H,

F4 = 6 H. Найти величину и направление силы Р, которую нужно приложить в точке О, чтобы тело было в равновесии.

Решение

Найдем равнодействующую R этой системы сходящихся сил с помощью проектирования всех их на оси системы координат. Получим

Rx = F1 cos90 + F2 cos 45 + F3 cos60 − F4 cos30 = −0,37(H ), Ry = F1 sin 90 + F2 sin 45 − F3 sin 60 − F4 sin 30 = −1,64(H ).

Модуль вектора R будет определен по теореме Пифагора R = 1,68 (H). Направление вектора можно определить углами

12