
Атомная физика и физика твёрдого тела
..pdfМинистерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
Томский государственный университет систем управления и радиоэлектроники
Кафедра физики
А.В. Лячин, Ю.П. Чужков
АТОМНАЯ ФИЗИКА И ФИЗИКА ТВЁРДОГО ТЕЛА
Учебно-методическое пособие по аудиторным практическим занятиям
и самостоятельной работе для студентов всех направлений подготовки
Томск
2018
Рецензент Ремпе Н. Г., д-р техн. наук, профессор кафедры физики
Томск. гос. ун-та систем упр. и радиоэлектроники
Лячин, Александр Владимирович
Атомная физика и физика твёрдого тела: учеб.-метод. пособие по аудиторным практ. занятиям и самостоятельной работе для студентов всех направлений подготовки / А.В. Лячин, Ю.П. Чужков. – Томск: Томск. гос. ун-т систем упр. и радиоэлектроники, 2018. – 147 с.
Содержит краткую теорию, примеры решения задач, тестовые задания, задачи для аудиторных практических занятий и самостоятельного решения, список рекомендуемой литературы, а также вопросы для самоконтроля по разделу «Атомная физика и физика твёрдого тела» дисциплины «Физика» («Физика для информатики», «Физика и естествознание» и т.п.).
Для студентов очной, очно-заочной и заочной форм образования всех направлений подготовки.
© Лячин А.В., Чужков Ю.П., 2018 © Томск. гос. ун-т систем упр.
и радиоэлектроники, 2018
ОГЛАВЛЕНИЕ
Введение........................................................................................................... |
5 |
|
1 МОДЕЛЬ АТОМА. ТЕОРИЯ БОРА. ХАРАКТЕРИСТИЧЕСКОЕ |
|
|
РЕНТГЕНОВСКОЕ ИЗЛУЧЕНИЕ |
|
|
1.1 |
Краткая теория........................................................................................... |
6 |
1.2 |
Примеры решения задач........................................................................... |
9 |
1.3 |
Задачи для решения на практических занятиях................................... |
18 |
1.4 |
Задачи для самостоятельного решения................................................. |
20 |
1.5 |
Вопросы для самоконтроля.................................................................... |
22 |
2 ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ |
|
|
2.1 |
Волновые свойства вещества. Волны де Бройля. Соотношение |
|
неопределенностей........................................................................................ |
24 |
|
2.1.1 Краткая теория..................................................................................... |
24 |
|
2.1.2 Примеры решения задач..................................................................... |
27 |
|
2.1.3 Задачи для решения на практических занятиях............................... |
34 |
|
2.1.4 Задачи для самостоятельного решения............................................. |
36 |
|
2.1.5 Вопросы для самоконтроля................................................................ |
38 |
|
2.2 |
Уравнение Шредингера. Частицы в потенциальной яме.................... |
39 |
2.2.1 Краткая теория..................................................................................... |
39 |
|
2.2.2 Примеры решения задач..................................................................... |
42 |
|
2.2.3 Задачи для решения на практических занятиях............................... |
46 |
|
2.2.4 Задачи для самостоятельного решения............................................. |
49 |
|
2.2.5 Вопросы для самоконтроля................................................................ |
52 |
|
2.3 |
Потенциальный барьер. Туннельный эффект...................................... |
52 |
2.3.1 Краткая теория..................................................................................... |
52 |
|
2.3.2 Примеры решения задач..................................................................... |
55 |
|
2.3.3 Задачи для решения на практических занятиях............................... |
59 |
|
2.3.4 Задачи для самостоятельного решения............................................. |
62 |
|
2.3.5 Вопросы для самоконтроля................................................................ |
66 |
|
2.4 |
Квантовые числа...................................................................................... |
66 |
2.4.1 Краткая теория..................................................................................... |
66 |
|
2.4.2 Примеры решения задач..................................................................... |
74 |
|
2.4.3 Задачи для решения на практических занятиях............................... |
83 |
|
2.4.4 Задачи для самостоятельного решения............................................. |
85 |
|
2.4.5 Вопросы для самоконтроля................................................................ |
86 |
|
3 ЭЛЕМЕНТЫ КВАНТОВОЙ СТАТИСТИКИ |
|
|
3.1 |
Краткая теория......................................................................................... |
88 |
3.2 |
Примеры решения задач......................................................................... |
91 |
3.3 |
Задачи для решения на практических занятиях................................... |
95 |
3.4 |
Задачи для самостоятельного решения................................................. |
97 |
3.5 |
Вопросы для самоконтроля.................................................................... |
99 |
|
3 |
|
4 ЭЛЕМЕНТЫ ФИЗИКИ ТВЁРДОГО ТЕЛА |
|
4.1 Тепловые свойства твёрдых тел.......................................................... |
101 |
4.1.1 Краткая теория.................................................................................. |
101 |
4.1.2 Примеры решения задач ................................................................... |
109 |
4.1.3 Задачи для решения на практических занятиях............................ |
116 |
4.1.4 Задачи для самостоятельного решения.......................................... |
118 |
4.1.5 Вопросы для самоконтроля ............................................................. |
120 |
4.2 Электропроводность твердых тел....................................................... |
121 |
4.2.1 Краткая теория.................................................................................. |
121 |
4.2.2 Примеры решения задач.................................................................. |
130 |
4.2.3 Задачи для решения на практических занятиях............................ |
135 |
4.2.4 Задачи для самостоятельного решения.......................................... |
138 |
4.2.5 Вопросы для самоконтроля ............................................................. |
140 |
5 ОТВЕТЫ К ЗАДАНИЯМ ДЛЯ ПРАКТИЧЕСКИХ ЗАНЯТИЙ |
|
И САМОСТОЯТЕЛЬНОЙ РАБОТЫ........................................................ |
142 |
Рекомендуемая литература........................................................................ |
146 |
4
Введение
Учебно-методическое пособие содержит краткую теорию, примеры решения задач, задачи для самостоятельного решения, тестовые задания и список рекомендуемой литературы по каждой теме практических занятий, а также вопросы для самоконтроля по разделу «Атомная физика и физика твёрдого тела» дисциплины «Физика» и предназначено для студентов очной формы, обучающихся по всем направлениям подготовки.
В разделе «Атомная физика и физика твёрдого тела» дисциплины «Физика» предметом изучения являются: строение атомов, их свойства и спектральные характеристики; представление об атомах и микрочастицах с точки зрения квантовой механики; статистические представления о коллективах микрочастиц и использование этих представлений для описания механизмов электропроводности и теплопроводности твёрдых тел. Знание раздела «Атомная физика и физика твёрдого тела», необходимо не только для общего представления о строении и свойствах вещества, но и пригодится в последующих специальных дисциплинах при решении конкретных прикладных задач.
Темы практических занятий: «Модель атома. Теория бора. Характеристическое рентгеновское излучение», «Волны де-Бройля. Соотношение неопределенностей», «Уравнение Шредингера. Частицы в потенциальной яме. Туннельный эффект», «Квантовые числа», «Квантовые статистики», «Тепловые свойства твёрдых тел», «Электропроводность твёрдых тел».
Процесс изучения раздела «Атомная физика и физика твёрдого тела» дисциплины «Физика» направлен на формирование у студентов всех направлений подготовки необходимых компетенций.
5
1 МОДЕЛЬ АТОМА. ТЕОРИЯ БОРА. ХАРАКТЕРИСТИЧЕСКОЕ РЕНТГЕНОВСКОЕ ИЗЛУЧЕНИЕ
1.1 Краткая теория
Постулаты Бора
1.Атом может длительное время находиться только в определенных, так называемых стационарных состояниях, соответствующих определенным квантовым условиям, характеризуемых дискрет-
ными значениями энергии E1, E2, Е3, ... В этих состояниях атом не излучает.
2.При переходе атома из стационарного состояния с большей
энергией E2 в стационарное состояние с меньшей энергией E1 происходит излучение кванта света (фотона) с энергией :
E2 E1.
Такое же соотношение выполняется и в случае поглощения, когда падающий фотон переводит атом с низшего энергетического уровня E1 на более высокий E2 (правило частот Бора).
Правило квантования орбитального момента импульса. Бор предположил, что электрон в атоме водорода движется только по тем круговым орбитам, для которых его момент импульса L по величине кратен постоянной Планка:
L n , или |
m r n , n = 1, 2, 3,…, |
(1.1) |
где n – квантовое число.
Полная энергия электрона в кулоновском поле ядра согласно модели Резерфорда – Бора
E E U |
m 2 |
|
|
|
1 |
|
Ze2 |
|
1 |
|
|
Ze2 |
, |
(1.2) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
к |
2 |
|
|
4 0 |
r |
|
|
4 0 |
2r |
|
|
|||||
|
|
|
|
|
|
|
||||||||||
а радиус n-й стационарной орбиты |
|
|
|
|
|
|
|
|
|
|||||||
|
rn |
|
4 0 2n2 |
. |
|
|
|
|
|
|
(1.3) |
|||||
|
|
|
mZe2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Радиус первой стационарной орбиты электрона в атоме водоро- |
||||||||||||||||
да (n = 1, Z = 1) равен |
r |
4 |
0 |
2 |
|
|
|
|
10 |
|
|
|
||||
|
|
|
|
|
0,529 10 |
м. Его называют |
||||||||||
|
|
|
|
|
|
|
|
|||||||||
|
1 |
|
me2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
первым боровским радиусом.
6
Энергия En электрона на n-й стационарной орбите в системе СИ равна:
Е |
me4 |
Z 2 |
. |
(1.4) |
|
|
|
|
|||
n |
32 0 |
2 |
п2 |
|
|
|
|
|
|||
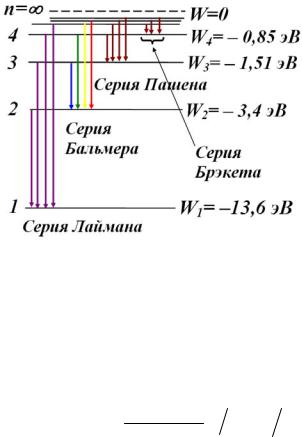
Эта формула описывает уровни энергии стационарных состояний электрона в водородоподобной системе. Для атома водорода схема энергетических уровней показана на рисунке 1.1. При n уровни энергии сгущается, а энергия стремится к предельному значению E 0.
Состояние атома с наименьшей энергией (n = 1) называют основным. Для атома водорода основному состоянию соответствует энергия Е1 13,6 эВ. Эта энергия (по модулю) является энергией
связи электрона в основном состоянии: Есв | Е1 | . Именно такую
энергию надо сообщить электрону в основном состоянии (n = 1), чтобы удалить его из атома водорода. По этой причине ее называют еще и энергией ионизации: Eион Eсв 13,6 эВ.
Рисунок 1.1 – Cхема энергетических уровней атома водорода
Энергия фотонов, излучаемых или поглощаемых при переходе системы из одного стационарного состояния в другое, в СИ согласно второму постулату Бора равна:
Еn j |
Еni |
|
me4Z 2 |
1 |
ni2 1 |
n2j , |
(1.5) |
32 2 02 2 |
7

где ni и n j – квантовые числа состояний, между которыми соверша-
ется переход.
Частота фотона:
|
me |
4 |
Z |
2 |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
||||||
Е2 Е1 32 |
3 |
|
n2 |
(1.6) |
|||||||
n2 |
. |
||||||||||
|
|
|
0 |
|
|
|
i |
|
j |
|
|
Постоянная Ридберга:
|
|
R |
|
|
me4 |
|
2,07 1016 |
рад/с, |
|
|
|
||||||
|
|
32 2 02 |
3 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
R |
R |
|
|
15 |
–1 |
|
R |
|
R |
|
|
R |
|
|
7 |
–1 |
|
|
3, 29 |
10 |
с , |
|
|
|
|
|
|
|
1,097 |
10 |
|
м . |
|||
|
|
|
|
|
|
|
|||||||||||
|
2 |
|
|
|
|
|
|
|
2 c |
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Обобщенная формула Бальмера: |
. |
|
|
|
|
|
|||||||||||
|
|
|
|
R 1 ni2 |
1 n2j |
|
|
|
|
(1.7) |
|||||||
Частоты, соответствующие серии Лаймана, возникают при пере- |
|||||||||||||||||
ходе электрона в состояние ni |
1 со всех вышележащих энергетиче- |
||||||||||||||||
ских уровней. Серии Бальмера соответствуют переходы в состояние с квантовым числом ni 2 из состояний n j 3, 4, 5, ... Серия Пашена
соответствует переходам электрона в состояние с квантовым числом ni 3 из состояний nj 4, 5, 6, ... (см. рисунок 1.1).
Характеристическое рентгеновское излучение. Английский физик Мозли установил в 1913 г. закон, связывающий частоты линий рентгеновского спектра с атомным номером Z испускающего их элемента (рисунок 1.2):
R Z 2 |
|
1 |
|
1 |
|
|
|
|
|
|
|
, |
(1.8) |
||||
|
n 2 |
|||||||
|
n 2 |
|
|
|
|
|||
|
|
i |
|
j |
|
|
|
|
где постоянная, учитывающая экранирующую роль электронов, окружающих ядро. Чем дальше электрон находится от ядра, тем эта постоянная больше.
Энергетические уровни в атоме обозначаются буквами K, L, M, N, … Частоты, соответствующие K-серии, возникают при переходе электрона в состояние ni 1 со всех вышележащих энергетических
уровней. L-cерии соответствуют переходы в состояние с квантовым
8
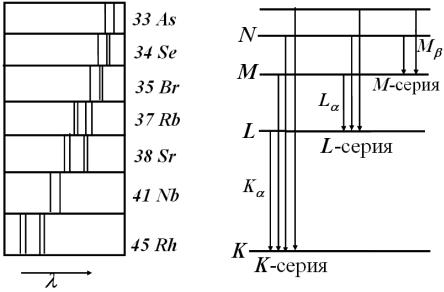
числом ni 2 из состояний n j 3, 4, 5, ... M-cерия соответствует переходам электрона в состояние с квантовым числом ni 3 из состояний nj 4, 5, 6, ... (см. рисунок 1.2).
Рисунок 1.2 – Спектральные линии характеристического рентгеновского излучения
Головная или α-линия каждой серии соответствует переходу электрона в состояние с квантовым числом ni из состояния
nj ni 1. Остальные линии в серии обозначаются по мере увеличения энергии (частоты) буквами греческого алфавита , , , , ...
1.2 Примеры решения задач
Задача 1. Имеется система (мезоатом), состоящая из ядра атома водорода (протона) и мюона (частицы с зарядом –e и массой 207me). Исходя из представлений теории Бора, определить: а) радиусы орбит мюона; сравнить радиус первой орбиты r1 с боровским радиусом r0 ;
б) энергию Eсв (в эВ) связи мюона с протоном в основном состоянии; в) скорость 1 мюона на первой орбите (сравнить со скоростью
электрона на первой орбите); г) число оборотов, которое успеет совершить мюон до своего распада (время жизни мюона = 2,2 мкс).
9
Дано: |
|
|
|
|
|
|
Решение. Для решения задачи вос- |
|||||||
|
|
|
|
|
|
|||||||||
m0 = mp = 1,67 10–27 кг |
пользуемся теорией Бора, воспроизведя |
|||||||||||||
m = 207 9,1 10–31 кг |
цепочку рассуждений, выполненных для |
|||||||||||||
q = –e |
|
|
|
|
|
атома водорода, применительно к мезо- |
||||||||
= 2,2 10–6 с |
атому. |
|
|
|
|
|
|
|||||||
r0 = 0,529 10–10 м |
|
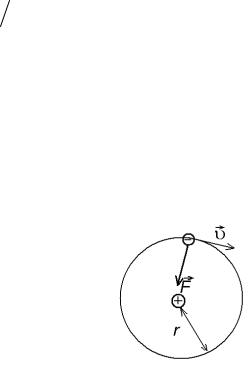
а) На мюон, находящийся на орбите |
||||||||||||
а) rn = ? |
r1 |
|
= ? |
(рисунок 1.3), |
|
действует сила |
Кулона |
|||||||
|
|
|
|
|
e2 |
|
|
|
||||||
r |
|
|
|
1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
|
0 |
|
|
|
Fк |
|
|
rn2 , |
|
которая является |
центро- |
|||
б) Eсв = ? |
|
|
4 0 |
|
||||||||||
в) v1 = ? |
|
v1 |
? |
стремительной силой: |
|
|||||||||
|
|
|
||||||||||||
|
v |
|
|
|
|
|
2 |
|
|
|
||||
г) N = |
|
|
1e |
|
|
Fк mмvn |
|
rn . |
|
|||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
По второму закону Ньютона |
|
|||||||
|
|
|
|
|
|
m v2 |
|
|||||||
|
|
|
|
|
|
|
|
1 |
|
e2 |
|
|
|
|
|
|
|
|
|
|
м n |
|
|
|
|
. |
|
(1) |
|
|
|
|
|
|
|
4 0 rn2 |
|
|||||||
|
|
|
|
|
|
rn |
|
|
|
|
|
|||
Согласно теории Бора момент импульса мюона квантуется:
|
|
mмvnrn n , |
(2) |
|
где n = 1, 2, … – главное квантовое число. |
|
|||
Решив совместно уравнения (1) и (2), найдем |
|
|||
радиусы орбит rn и скорости мюона vn |
на этих ор- |
|
||
битах. |
|
|
|
|
Выразим скорость из уравнения (2): |
|
|
||
v |
n |
|
(3) |
|
|
|
|
||
n |
mмrn |
|
Рисунок 1.3 |
|
|
|
|||
и подставим в уравнение (1), получаем: |
|
|
||
|
m |
n2 2 |
|
1 e2 |
|
||
|
м |
|
|
|
|
rn2 . |
|
|
rn |
mм2 rn2 |
4 0 |
|
|||
|
Следовательно, |
|
|
|
|
|
|
|
rn |
4 0n2 2 |
(4) |
||||
|
|
m e2 . |
|||||
|
|
|
|
м |
|
||
|
Очевидно, что радиус |
орбиты электрона |
в атоме водорода |
||||
re |
4 0n2 2 . |
|
|
|
|
|
|
n |
m e2 |
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
10
