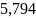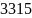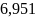лаб16
.docxФедеральное агентство связи
Ордена Трудового Красного Знамени
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
Кафедра «Теория электрических цепей»
Отчет по лабораторной работе №16
по дисциплине «Электротехника» на тему:
«Исследование на ЭВМ резонансных явлений в пассивном и активном последовательном колебательном контуре»
Выполнил: студент группы БСТ21
Руководитель: Волков А.С.
Москва, 2022 г.
Оглавление
Ход выполнения работы 3
Схемы и графики из Micro-Cup 5
Цель: С помощью программы Micro-Cap исследовать характеристики одиночного последовательного пассивного и активного колебательного контура при различных добротностях.
Ход выполнения работы
Расчеты:
Резонансная
частота последовательного колебательного
контура:
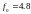 кГц
кГц
Из
формулы резонансной частоты, выражая
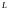 получим:
получим: 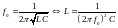 .
.
Выбрав
из интервала величину ёмкости C∈[10;
40] нФ C
= 30 нФ,
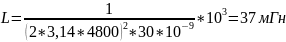
В дальнейших расчетах будут использоваться эти значения
ρ
— характеристическое сопротивление,
=
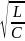 ;
;
=
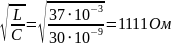 .
.
Q
— добротность, Q=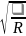 – добротность;
– добротность;
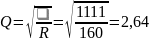 ,
при R
= 160 Ом
,
при R
= 160 Ом
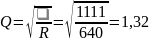 ,
при R
= 640 Ом
,
при R
= 640 Ом
f1
— нижнюю граничную частоту;
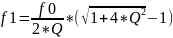 ;
;
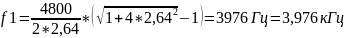 ,
при R
= 160 Ом
,
при R
= 160 Ом
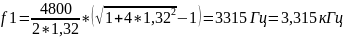 ,
при R
= 640 Ом
,
при R
= 640 Ом
f2
— верхнюю граничную частоту;
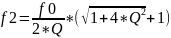 ;
;
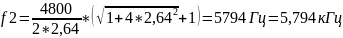 ,
при R
= 160 Ом
,
при R
= 160 Ом
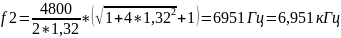 ,
при R
= 640 Ом
,
при R
= 640 Ом
П
— абсолютную полосу пропускания;
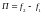 ;
;
П = 5,794 – 3,976 = 1,818 кГц, при R = 160 Ом
П = 6,951 – 3,315 = 3,636 кГц, при R = 640 Ом
I0
— модуль входного тока при резонансе;
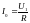 ;
;
I1
=
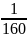 = 0,00625
А
= 6,25 мА,
,
при R
= 160 Ом
= 0,00625
А
= 6,25 мА,
,
при R
= 160 Ом
I2
=
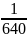 = 0,0015625 А
= 1.563 мА,
,
при R
= 640 Ом
= 0,0015625 А
= 1.563 мА,
,
при R
= 640 Ом

при f0 = 5k, G = 0,1 см, C2 = 1мкФ C1 = 10,14мкФ.
По предварительному расчету: U1 = 1 B, f0 = 4,8 кГц, С = 30 нФ, L = 37 мГн |
|||||||
R, Ом |
|
Q |
f1, кГц |
f2, кГц |
П, кГц |
I0, мА |
f0, кГц |
160 |
|
|
|
|
1,818 |
6,25 |
4,8 |
640 |
|
1,32 |
|
|
3,636 |
1,563 |
4,8 |
Гиратор |
|||||||
По предварительному расчету: U1 = 1 B, f0 = 5 кГц, С2 = 1 мкФ, G = 0.1 Cм |
|||||||
R, Ом |
С1, мкФ |
||||||
0,1 |
10,14 |
||||||
Таблица 1 - Результаты предварительного расчета
Схемы и графики из Micro-Cup
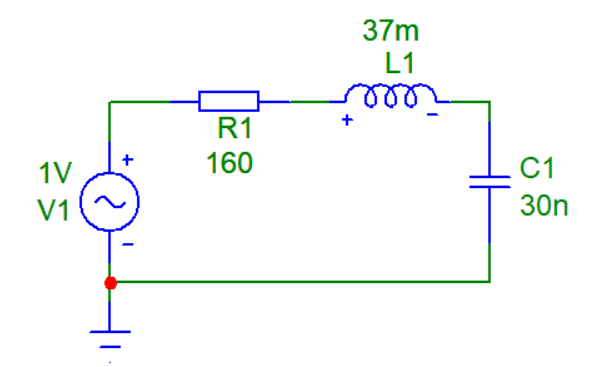
Рисунок 6 – Пассивный последовательный колебательный контур
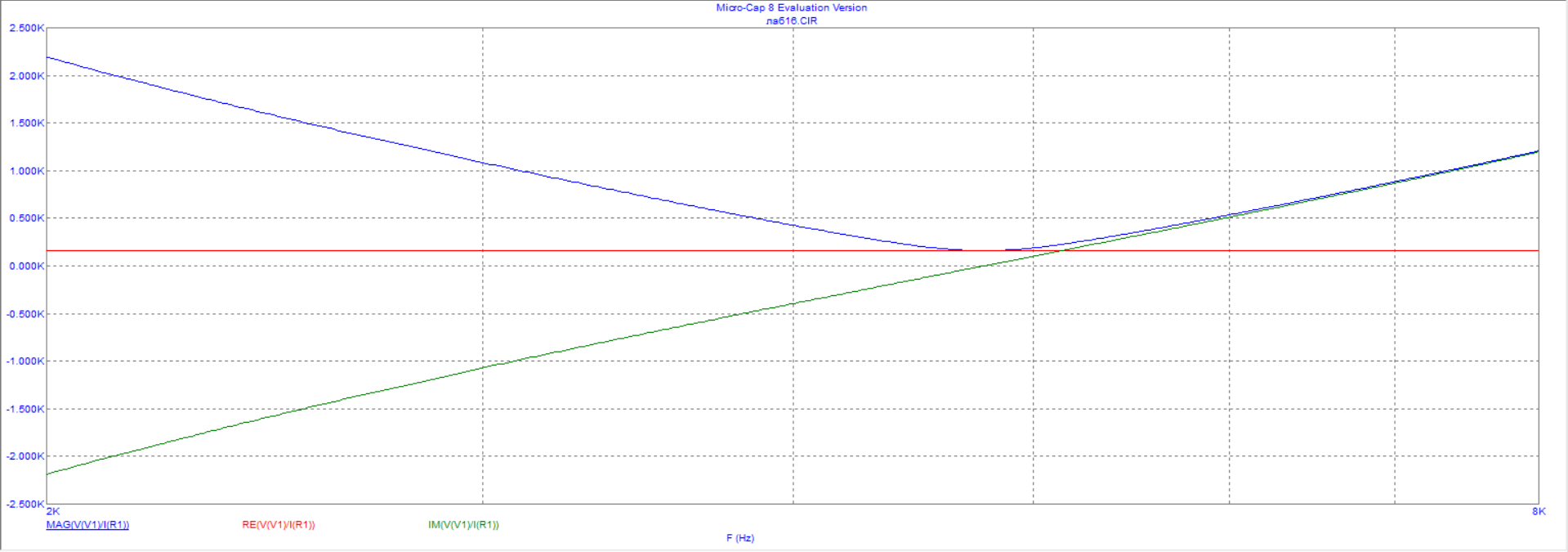
Рисунок 7 - Зависимость модуля, действительной и мнимой части входного сопротивления от частоты при R=160
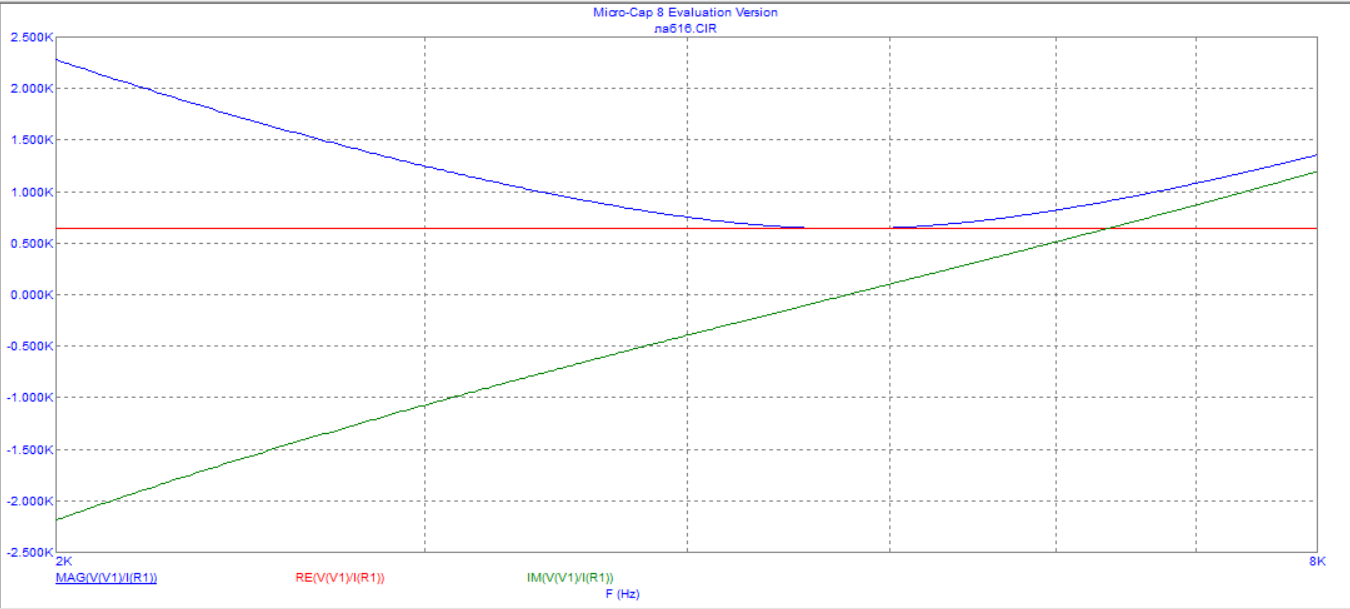
Рисунок 8 - Зависимость модуля, действительной и мнимой части входного сопротивления от частоты при R=640
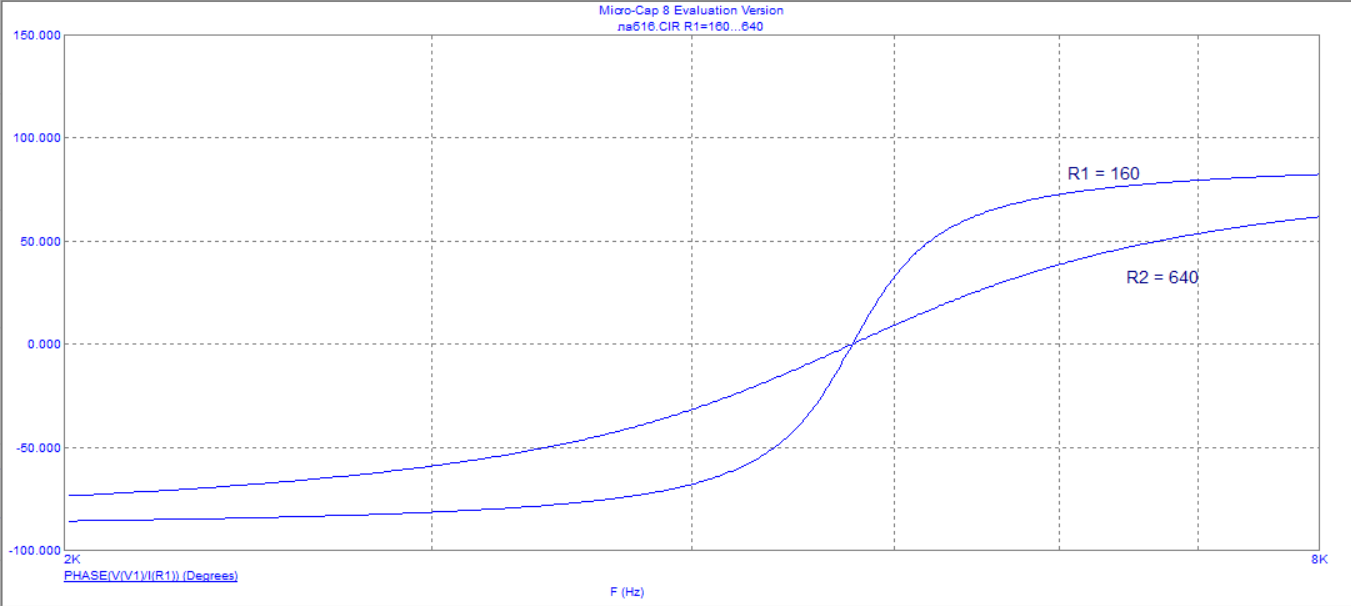
Рисунок 9 - Зависимость фазы входного сопротивления от частоты
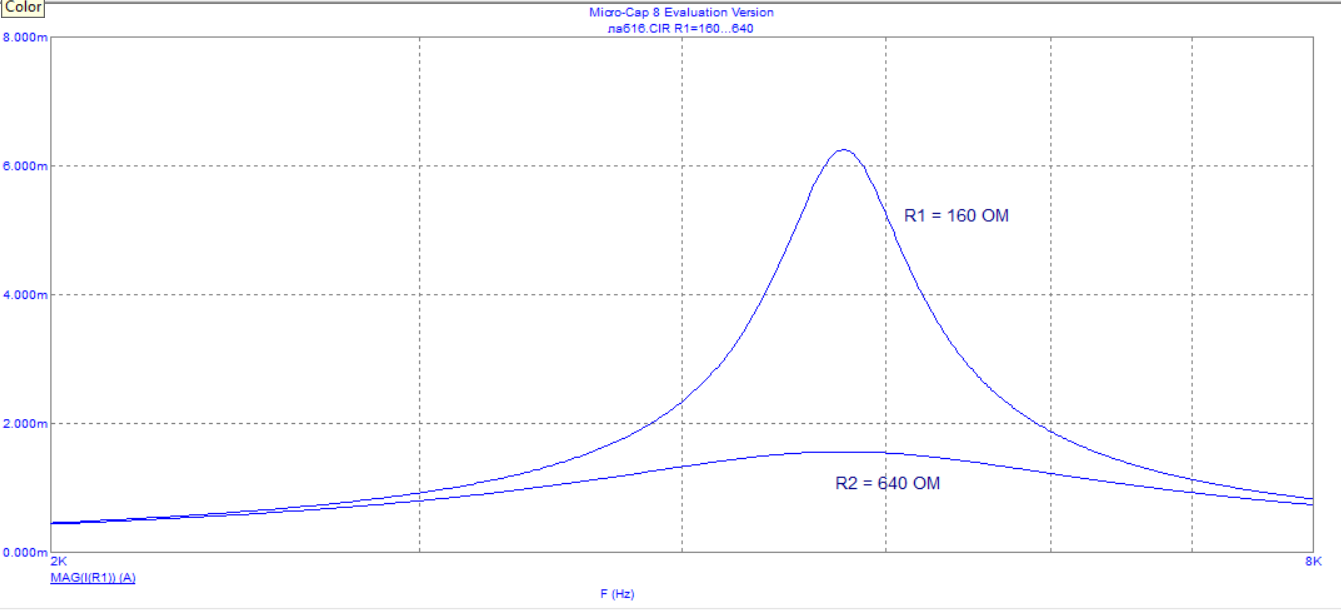
Рисунок 10 - Зависимость модуля входного тока от частоты
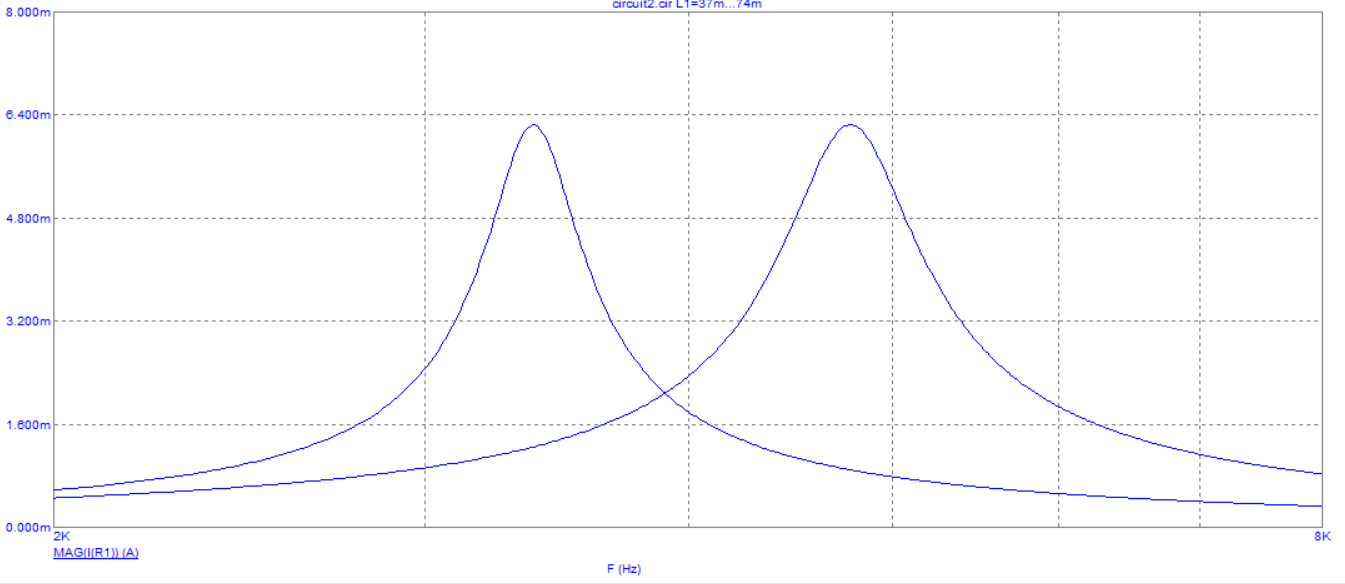
Рисунок 11 - Зависимость модуля входного тока от частоты (При R1 = 160, L1 = L, L2 = 2L)
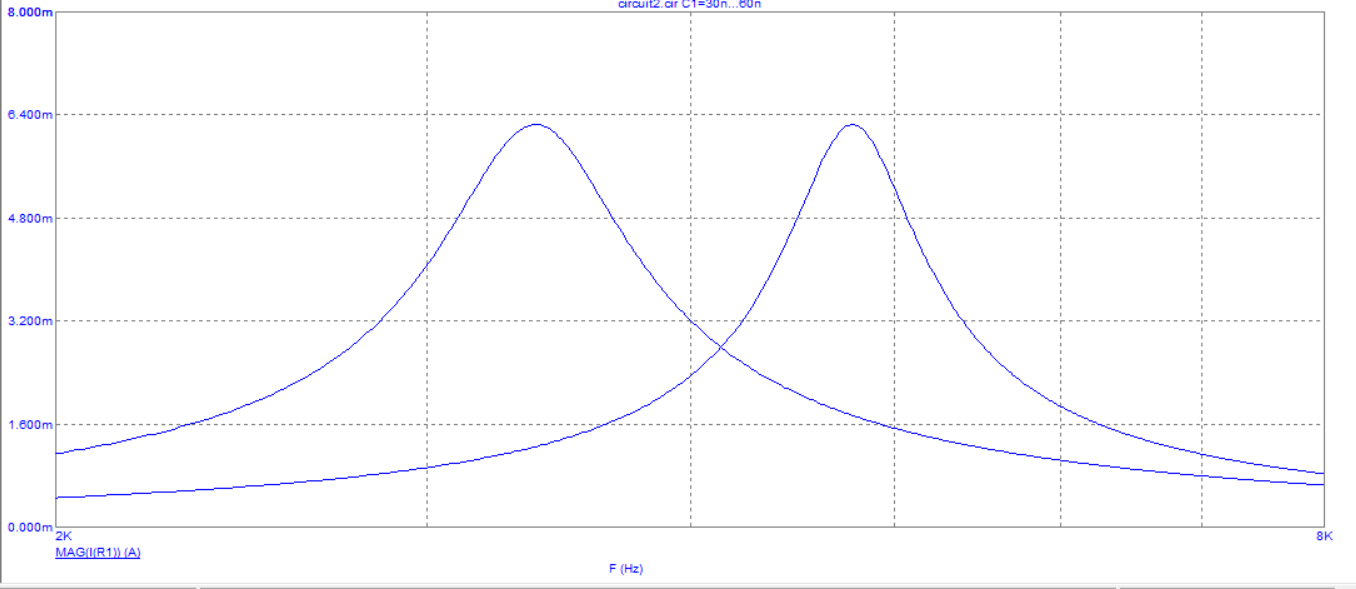
Рисунок 12 - Зависимость модуля входного тока от частоты (При R1 = 160, C1 = C, C2 = 2C)

Рисунок 13 – Схема с гиратором
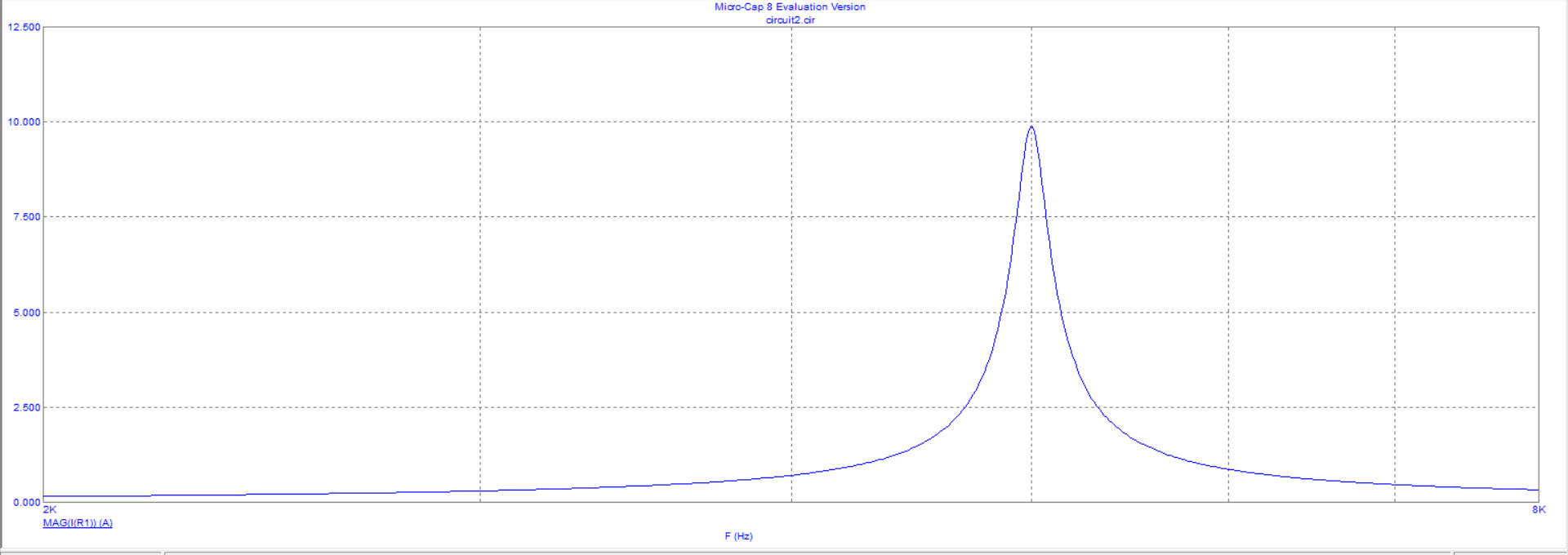
Рисунок 14 - Зависимость модуля входного тока от частоты в схеме с гиратором при R1 = 0.1 Ом
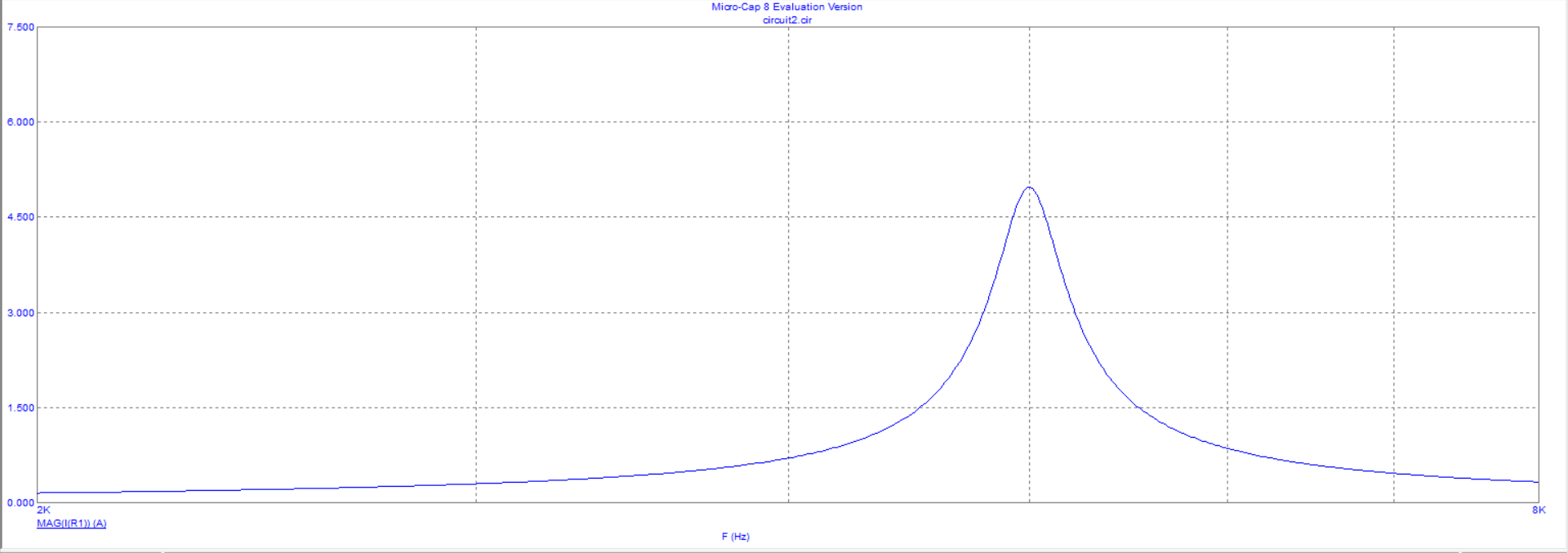
Рисунок 15 - Зависимость модуля входного тока от частоты в схеме с гиратором при R1 = 0.2 Ом
Получено экспериментально: |
|||||||
R, Ом |
f0, кГц |
I0, мА |
f1, кГц |
f2, кГц |
П, кГц |
Q |
|
160 |
4,8 |
6,249 |
3,975 |
5,797 |
1,822 |
2,635 |
|
640 |
4,8 |
1,562 |
3,312 |
6,956 |
3,644 |
1,317 |
|
Гиратор |
|||||||
Получено экспериментально: |
|||||||
R, Ом |
f0, кГц |
||||||
0,1 |
5 |
||||||
Таблица 2 - Результаты эксперимента
Вывод: с помощью программы Micro-Cap исследовал характеристики одиночного последовательного пассивного и активного колебательного контура при различных добротностях.

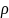 ,
Ом
,
Ом