
- •Часть 1 содержит лекции по темам: «Механика», «Электростатика и постоянный ток», «Магнитное поле и электромагнитная индукция».
- •Лекция 1
- •1. Кинематика поступательного движения
- •Механическое движение
- •1.2. Основные понятия и определения
- •Эти уравнения движения эквивалентны векторному уравнению
- •1.3. Скорость
- •1.4. Ускорение
- •Лекция 2
- •2. Кинематика вращательного движения
- •2.1. Вращательное движение
- •2.2. Угловой путь. Угловая скорость. Угловое ускорение
- •2.3. Соотношение между угловыми и линейными величинами
- •Нормальное ускорение равно
- •Как нормальное, так и касательное ускорение растет линейно с увеличением расстояния r от точки до оси вращения.
- •Лекция 3
- •3. Динамика поступательного движения
- •3.1. Сила. Первый закон ньютона
- •Виды сил
- •Первый закон Ньютона
- •3.2. Второй закон ньютона. Масса. Импульс
- •2Ой закон Ньютона. Ускорение, приобретаемое телом, совпадает по направлению с действующей на него силой и равно отношению этой силы к массе тела
- •Выражение (3.2.3) можно записать в виде:
- •3.3. Третий закон ньютона
- •Третий закон
- •3.4. Закон сохранения импульса
- •Лекция 4
- •4. Динамика вращательного движения
- •4.1. Момент инерции относительно оси вращения
- •4.2. Момент силы относительно оси вращения
- •4.3. Момент импульса. Основное уравнение динамики вращательного движения
- •4.4. Закон сохранения момента импульса
- •Лекция 5
- •5. Энергия. Работа. Мощность
- •5.1. Способы вычисления работы
- •5.2. Мощность
- •5.3. Кинетическая энергия
- •5.4. Потенциальная энергия
- •Следовательно для тела, находящегося в поле тяготения Земли
- •По третьему закону Ньютона для преодоления силы упругости надо приложить силу
- •5.5. Закон сохранения энергии
- •6.2. Постулаты специальной теории относительности
- •Кто понимает теорию относительности?
- •Был этот мир глубокой тьмой окутан.
- •6.3. Преобразования лоренца
- •Аналогично можно получить
- •6.4 Закон сложения скоростей
- •Разделив уравнение (6.4.1) на (6.4.2) получим
- •Лекция 7
- •7. Следствия из преобразований лоренца
- •7.1. Длина тела в различных исо
- •7.2. Длительность событий в различных исо
- •Воспользуемся формулами преобразования времени
- •Интервал между событиями
- •7.3. Основной закон релятивистской динамики материальной точки
- •7.4. Взаимосвязь массы и энергии
- •Для изменения кинетической энергии необходимо совершить работу
- •7.5. Значение теории относительности
- •Лекция 8 Электрическое поле
- •8.1. Электрический заряд
- •Линейная плотность электрических зарядов.
- •8.2. Закон Кулона
- •8.2.1. Закон Кулона для точечных зарядов
- •8.2.2. Закон Кулона для заряженных тел
- •8.3. Электрическое поле
- •8.3.1. Понятие электрического поля
- •8.3.2. Напряженность электрического поля
- •8.3.3. Графическое представление электрического поля
- •9.2. Поток вектора электрического смещения (индукции)
- •9.3. Теорема Остроградского-Гаусса
- •9.4. Применение теоремы Остроградского–Гаусса
- •9.4.1. Поле равномерно заряженной сферы
- •9.4.2. Поле равномерно заряженного шара
- •9.4.3. Поле бесконечного равномерно заряженного цилиндра
- •9.4.4. Поле бесконечной равномерно заряженной плоскости
- •Лекция 10 потенциал электростатического поля
- •10.1. Работа сил электростатического поля
- •10.2. Электрический потенциал. Разность потенциалов
- •1 КэВ (килоэлектронвольт) - 103 эВ;
- •1 МэВ (мегаэлектронвольт) - 106 эВ;
- •10.3. Связь между напряженностью электрического поля и потенциалом
- •10.4. Эквипотенциальные поверхности
- •Лекция 11 проводники в электрическом поле
- •11.1. Распределение зарядов в проводнике
- •11.2. Электрическая емкость уединенного проводника
- •11.3. Конденсаторы
- •11.3.1. Плоский конденсатор
- •11.3.2. Цилиндрический конденсатор
- •11.3.3. Сферический конденсатор
- •11.3.4. Соединения конденсаторов
- •11.4. Энергия заряженного проводника
- •11.5. Энергия заряженного конденсатора
- •11.6. Энергия электрического поля
- •Лекция 12 понятие об элекрическом токе
- •12.1. Понятие об электрическом токе
- •12.2. Сила и плотность тока
- •12.3. Закон ома в дифференциальном виде
- •12.4. Электродвижущая сила
- •12.5. Закон ома в интегральной форме
- •12.6. Зависимость электропроводности от температуры
- •12.7. Закон джоуля – ленца в дифференциальной форме
- •12.8. Работа и мощность электрического тока
- •Лекция 13 законы кирхгофа
- •Лекция 14 диэлектрики в электрическом поле
- •14.1. Дипольные моменты молекул диэлектрика
- •14.2. Поляризация диэлектриков
- •14.3. Электрическое поле диэлектрика
- •14.4. Сегнетоэлектрики
- •15.2. Закон Ампера
- •15.3. Закон Био-Савара-Лапласа
- •15.4. Магнитный поток
- •15.5. Магнитный момент контура с током
- •15.6. Теорема Гаусса для магнитного поля
- •Лекция 16 принцип суперпозиции и его применение
- •16.1. Принцип суперпозиции
- •16.2. Магнитное поле прямолинейного проводника с током
- •16.3. Магнитное поле кругового тока
- •16.4. Магнитное поле в центре прямоугольной рамки
- •1 М 6.5. Закон полного тока
- •16.6. Магнитное поле соленоида (катушки)
- •16.7. Магнитное поле тороида
- •Лекция 17 действие магнитного поля на электрический ток
- •17.1. Взаимодействие параллельных токов
- •17.2. Вращение рамки с током в магнитном поле
- •17.3. Работа магнитного поля по перемещению проводника с током
- •17.4. Работа магнитного поля по перемещению контура с током
- •Лекция 18 действие магнитного поля на движущийся заряд
- •18.1. Сила Лоренца
- •18.2. Движение заряженной частицы в магнитном поле
- •18.3. Масс-спектрометр
- •18.4. Эффект Холла
- •18.5. Ускорители
- •Лекция 19 явление электромагнитной индукции
- •19.1. Опыты Фарадея
- •19.2. Основной закон электромагнитной индукции
- •19.3. Эдс индукции при вращении рамки в магнитном поле
- •19.4. Эдс индукции в движущемся проводнике
- •19.5. Развернутая формула основного закона электромагнитной индукции
- •Лекция 20 явление самоиндукции
- •20.1. Индуктивность контура
- •20.2. Самоиндукция
- •20.3. Индуктивность катушки
- •20.4. Токи при замыкании и размыкании цепи
- •20.5. Энергия магнитного поля
- •Лекция 21
- •21.1. Взаимная индукция
- •21.2. Взаимная индуктивность двух катушек
- •21.3. Трансформатор
- •21.4. Вихревые токи
- •21.5. Скин-эффект
- •Лекция 22 магнитные свойства твердых тел
- •22.1. Магнитные моменты электрона и атома
- •22.2. Диамагнетики
- •22.3. Парамагнетики
- •22.4. Ферромагнетики
- •Свойства ферромагнетиков
- •Лекция 23 ток смещения
- •Лекция 24 основы теории максвелла электромагнитного поля
- •24.1. Первое уравнение Максвелла
- •24.2. Второе уравнение Максвелла
- •24.3. Третье и четвертое уравнения Максвелла
- •24.4. Первое и второе уравнения Максвелла в дифференциальной форме
- •24.5. Третье и четвертое уравнения Максвелла в дифференциальной форме
- •Литература
- •Оглавление
15.4. Магнитный поток
а )
В однородном
магнитном поле с индукцией
расположена плоскость, площадь поверхности
которой равна S
(рис. 15.4.1).
)
В однородном
магнитном поле с индукцией
расположена плоскость, площадь поверхности
которой равна S
(рис. 15.4.1).
Угол между нормалью
![]() к поверхности и вектором магнитной
индукции
к поверхности и вектором магнитной
индукции
![]() обозначен
.
обозначен
.
Магнитный поток
![]() ,
сцепленный с рассматриваемой поверхностью,
равен
,
сцепленный с рассматриваемой поверхностью,
равен
![]() .
(15.4.1)
.
(15.4.1)
Магнитное поле
изображают линиями индукции так, что
через единицу площади поверхности
проходит количество линий индукции
численно равное модулю магнитной
индукции
![]() .
.
Произведение
![]() равно числу линий индукции, проходящих
через площадь поверхности S.
Произведение
равно числу линий индукции, проходящих
через площадь поверхности S.
Произведение
![]() равно
проекции вектора
на направление нормали.
равно
проекции вектора
на направление нормали.
Учитывая все, выше сказанное, получаем в соответствии с формулой (15.4.1): магнитный поток показывает число линий индукции, проходящих через площадь S в направлении перпендикулярном поверхности. Единица измерения магнитного потока в СИ
![]() =1
Вб (вебер).
=1
Вб (вебер).
1 вебер – это магнитный поток, проходящий сквозь плоскую поверхность площадью 1 м2, расположенную перпендикулярно линиям индукции однородного магнитного поля с магнитной индукцией 1 Тл.
б) Рассмотрим
поверхность
площадью
![]() ,
расположенную в неоднородном магнитном
поле. Выберем элементарную площадь
поверхности
,
для которой магнитное поле можно считать
однородным (рис. 15.4.2). В этом случае в
соответствии с формулой (15.4.1) для
однородного поля можно записать выражение
для элементарного магнитного потока:
,
расположенную в неоднородном магнитном
поле. Выберем элементарную площадь
поверхности
,
для которой магнитное поле можно считать
однородным (рис. 15.4.2). В этом случае в
соответствии с формулой (15.4.1) для
однородного поля можно записать выражение
для элементарного магнитного потока:
![]()
и ли
ли
![]() ,
,
где
![]() – проекция
магнитной индукции на направление
нормали, или
– проекция
магнитной индукции на направление
нормали, или
![]() ,
(15.4.2)
,
(15.4.2)
здесь
![]() ,
,
![]() - нормаль к поверхности.
- нормаль к поверхности.
Для определения магнитного потока через поверхность площадью S необходимо проинтегрировать выражение (15.4.2)
![]() .
(15.4.3)
.
(15.4.3)
15.5. Магнитный момент контура с током
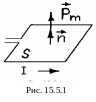
Магнитное поле контура с током характеризуется магнитным моментом, который определяется по формуле
![]() .
.
Модуль магнитного момента равен произведению силы тока I на площадь S, охватываемую контуром. Магнитный момент направлен по нормали к поверхности, охватываемой проводником с током (рис. 15.5.1). Направление магнитного момента можно определить по правилу правого винта: если головка винта поворачивается по направлению тока в контуре, то острый конец винта показывает направление магнитного момента. Модуль магнитного момента рассчитывают по формуле
![]() .
.
Единица измерения
магнитного момента в СИ равна![]() .
На рис. 15.5.1 контур с током имеет
прямоугольную форму; все вышеизложенное
справедливо для контура любой формы.
.
На рис. 15.5.1 контур с током имеет
прямоугольную форму; все вышеизложенное
справедливо для контура любой формы.
15.6. Теорема Гаусса для магнитного поля
Аналогично теореме Остроградского – Гаусса для электрического поля существует теорема Гаусса для магнитного поля.
В ыведем
теорему Гаусса для магнитного поля.
Рассмотрим частный случай: в однородном
магнитном поле с индукцией
ыведем
теорему Гаусса для магнитного поля.
Рассмотрим частный случай: в однородном
магнитном поле с индукцией![]() находится сфера (рис .15.6.1). Вычислим
поток магнитной индукции через замкнутую
сферическую поверхность. Магнитный
поток численно равен количеству линий
индукции магнитного поля, пересекающих
поверхность сферы.
находится сфера (рис .15.6.1). Вычислим
поток магнитной индукции через замкнутую
сферическую поверхность. Магнитный
поток численно равен количеству линий
индукции магнитного поля, пересекающих
поверхность сферы.
Количество выходящих из сферы линий индукции берут со знаком плюс, а число входящих в сферу линий индукции со знаком минус. Очевидно, число входящих в сферу линий индукции магнитного поля будет равно числу выходящих из нее линий индукции, т.к. линии индукции магнитного поля всегда замкнутые.
Алгебраическая сумма количества линий магнитной индукции, пересекающих сферу, будет равна нулю.
Аналогичный результат получится для тела любой формы и для тела, находящегося в неоднородном магнитном поле.
Обобщая все случаи математически, можно записать
![]() .
(15.6.1)
.
(15.6.1)
Теорема Гаусса для магнитного поля: магнитный поток через произвольную замкнутую поверхность равен нулю.
Магнитный поток можно записать в интегральной форме
![]()
(15.6.2)
Подставляя формулу магнитного потока (15.6.2) в выражение теоремы Гаусса (15.6.1), получаем
![]() (15.6.3)
(15.6.3)
Выражение (15.6.3) является формулой теоремы Гаусса в интегральном виде.
Теорема Гаусса отражает следующие экспериментальные факты: в природе нет магнитных зарядов и линии индукции магнитного поля всегда замкнутые.
Магнитное поле называется вихревым, т.к. его линии индукции всегда замкнутые.
