12.5. Закон ома в интегральной форме

Если в проводнике действуют кулоновские и сторонние силы, то результирующая напряженность Е поля будет равна векторной сумме и , т.е.

.

Подставив это выражение в формулу (12.3.9), получим

, но .

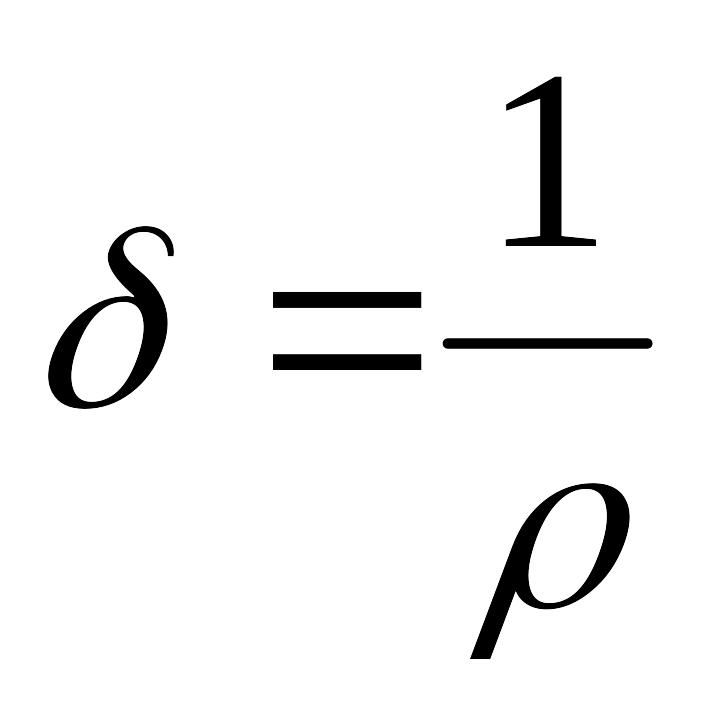Тогда

.

Умножим скалярно обе части равенства на вектор , численно равный элементу длины проводника и направленный по касательной к проводнику и совпадающий с вектором плотности тока :

.

Так как скалярное произведение совпадающих по направлению векторов и равно произведению их модулей, то предыдущее выражение перепишется в виде

. (12.5.1)

Подставляя и произведя интегрирование по длине проводника от сечения 1 до некоторого сечения 2 и учитывая, что сила тока во всех сечениях проводника одинаковая, получаем

.

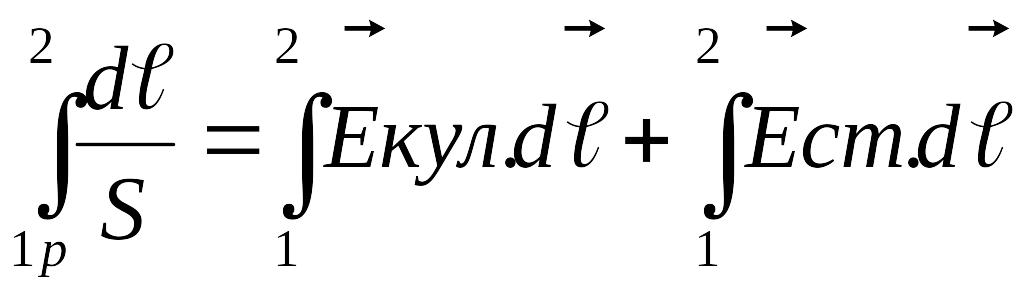Рассмотрим подробнее физический смысл всех членов полученного уравнения. Из электростатики известно, что

поэтому

, где и - значение потенциала в точках 1 и 2.

Из формулы (12.4.1) вытекает, что

.

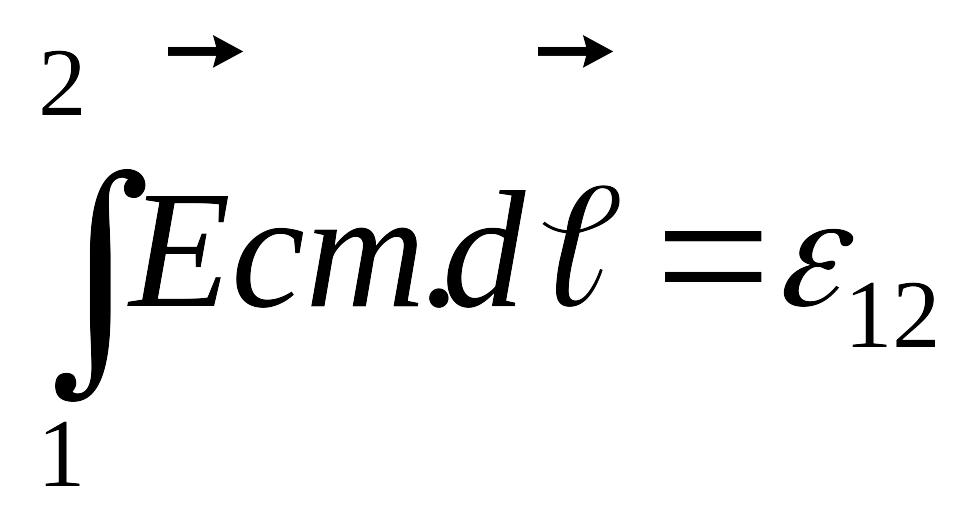Электродвижущая сила численно равна работе, совершаемой сторонними силами при перемещении по проводнику единичного положительного заряда из точки 1 в точку 2. Эта работа производится за счет энергии, вырабатываемой в источнике.

Если проводник однородный и имеет одинаковое сечение , то

можно записать , где - длина проводника.

Величина

(12.5.2)

называется сопротивлением проводника (в электротехнике эта величина называется омическим сопротивлением).

Значит - сопротивление участка 1-2.

Тогда выражение (12.5.1) можно записать

. (12.5.3)

Произведение силы тока на сопротивление участка цепи равно сумме разности потенциалов на этом участке и ЭДС всех источников электрической энергии, включенных на данном участке цепи.

Это утверждение есть закон Ома в интегральном виде для участка цепи, содержащего ЭДС (рис. 12.5.1).

П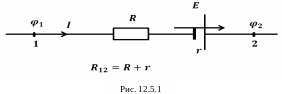 роизведение силы тока на сопротивление цепи, по которому протекает этот ток, называется падением напряжения на участке цепи. Обозначим падение напряжения на участке цепи буквой U. Тогда

и (12.5.4)

Сила тока на участке цепи, не содержащем ЭДС, прямо пропорциональна падению напряжения на этом участке цепи и обратно пропорциональна сопротивлению этого участка цепи.

Выражение (12.5.4) - тоже закон Ома в интегральном виде для произвольного участка цепи.

Из выражения (12.5.3) вытекает, что падение напряжения - это сумма работ сторонних и кулоновских сил по перемещению положительного заряда на участке цепи. Падение напряжения на концах участка цепи равно разности потенциалов только тогда, когда на этом участке нет ЭДС.

Действительно, если , то из выражения (12.5.3)

, (12.5.5)

но

или .

Если электрическая цепь замкнута, то точки 1 и 2 совпадают, так что , a общее сопротивление всей цепи.

Поэтому выражение (12.5.1) запишется

, (12.5.6)

где - алгебраическая сумма всех ЭДС, действующих в этой цепи.

Сопротивление всего контура разобьем на два слагаемых: на сопротивление внешней части цепи и сопротивление источника тока (внутреннее сопротивление источника тока).

Тогда и выражение (12.5.6) запишется

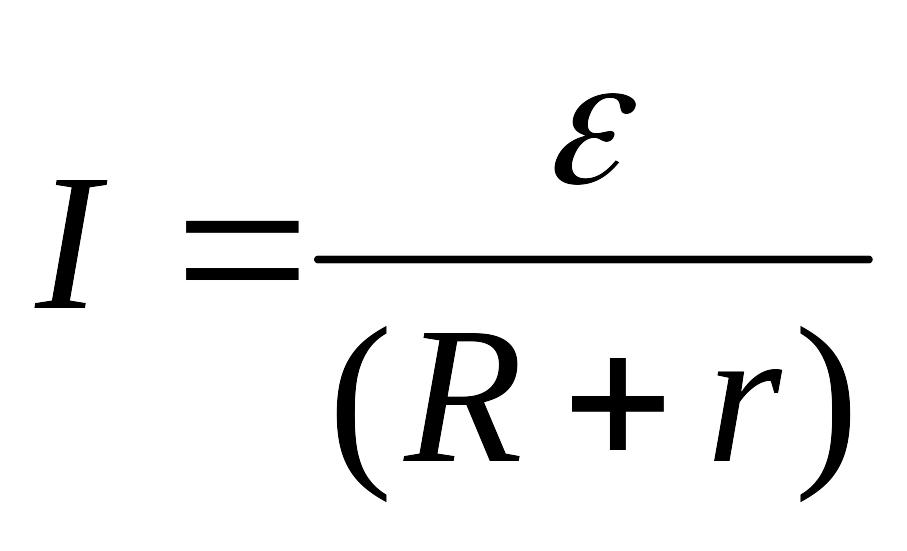. (12.5.7)

Выражение (12.5.7) - это закон Ома в интегральном виде для замкнутой цепи, который читается так: сила тока в замкнутой электрической цепи прямо пропорциональна действующей ЭДС в цепи и обратно пропорциональна сумме сопротивлений внешней и внутренней части цепи.

Во внутренней части цепи действуют сторонние силы, под действием которых электрические заряды движутся в сторону, противоположную направлению электростатических сил, а вне источника ЭДС, или во внешней части цепи - в направлении электростатических сил. Точки, разделяющие внешнюю и внутреннюю цепи, называются полюсами источника ЭДС. Полюс с более высоким потенциалом называют положительным, а с более низким - отрицательным. За направление ЭДС принимают направление, в котором перемещаются положительные заряды. Это означает, что ЭДС направлена внутри источника от отрицательного полюса к положительному, как показано на рис. 12.5.1.

Выражение (12.5.7) можно переписать в виде

,

где - падение напряжения на внешнем участке цепи, т.е. это работа, совершаемая полем по перемещению единичного положительного заряда по внешней части цепи;

- падение напряжения внутри источника тока, т.е. работа по перемещению единичного заряда внутри источника тока.

.

Отсюда вытекает, что ЭДС численно равна работе, совершаемой сторонними силами при перемещении единичного положительного заряда по всей замкнутой цепи.

ЭДС - энергетическая характеристика источника электрической энергии. Если цепь разомкнута и, следовательно, в ней отсутствует ток , то по формуле (12.5.3)

.

Это означает, что для нахождения ЭДС источника тока следует измерить разность потенциалов на его клеммах при разомкнутой внешней цепи.

Сопротивление проводника в СИ измеряется в омах. Сопротивление участка цепи равно 1-му если при токе в 1 А падение напряжения на этом участке равно 1 В.

Удельное сопротивление ρ в СИ измеряется в Ом*м. На практике его часто измеряют в Ом*cм (1 Ом*см = 0,01 Ом*м).