8.3.3. Графическое представление электрического поля

Поскольку электрическое поле является векторным, его можно изображать в различных точках стрелками различной длины в соответствии с величинами напряженностей. Однако этот способ неудобен, так как векторы напряженности при этом накладываются друг на друга и при большом числе точек весь рисунок будет испещрен стрелками. М. Фарадей предложил более удобный способ изображения поля - метод силовых линий.

Силовыми линиями (линиями напряженности) называются линии, проведенные в электрическом поле так, что касательные к ним в каждой точке пространства совпадают по направлению с вектором напряженности поля (рис. 8.3.6).

Силовые линии проводятся так, чтобы указывать направление силы, действующей в данном поле на положительный пробный заряд. Силовые линии точечного положительного заряда радиально расходятся от заряда, а точечного отрицательного заряда - сходятся к заряду (рис. 8.3.7).

Именно в таком направлении будут действовать силы на положительный пробный заряд.

Рис. 8.3.6

Условились наносить силовые линии с таким расчетом, чтобы число линий, исходящих от положительного заряда или заканчивающихся на отрицательном заряде, было пропорционально величине этого заряда. Поэтому, чем теснее расположены силовые линии, тем сильнее электрическое поле в этой области.

На рис. 8.3.8 показаны силовые линии поля, созданного двумя зарядами противоположного знака (см. рис. 8.3.8, а), поля, созданного двумя зарядами одноименного знака (см. рис.8.3.8, б), и поля между двумя параллельными противоположно заряженными пластинами (см. рис.8.3.8, в).

Рис. 8.3.7

Силовые линии обладают следующими свойствами.

1. Указывают направление напряженности электрического поля; в любой точке напряженность поля направлена по касательной к силовой линии.

2. Проводятся так, чтобы напряженность электрического поля была пропорциональна числу линий, проходящих через единичную площадку, перпендикулярную линиям.

3. Начинаются на положительных зарядах и заканчиваются на отрицательных зарядах либо уходят в бесконечность.

4. Никогда не пересекаются, не замыкаются сами на себя (не образуют замкнутых петель). Поэтому электростатическое поле есть поле безвихревое или потенциальное.

Силовые линии не следует отождествлять с траекторией движения в электрическом поле легких заряженных частиц. Траектория частиц обладает тем свойством, что в каждой ее точке по касательной к ней направлена скорость частицы. По касательной же к силовой линии направлена сила, действующая со стороны поля на частицу, а также ускорение частицы.

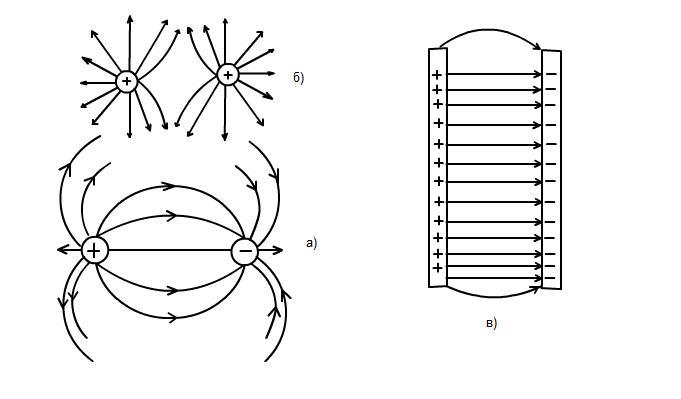
Рис. 8.3.8

Лекция 9

9. ТЕОРЕМА ОСТРОГРАДСКОГО-ГАУССА

И ЕЕ ПРИМЕНЕНИЕ

9.1. Вектор электрического смещения (индукции)

Напряженность электрического поля зависит от свойств среды, в которой поле образуется. Эта зависимость учитывается, как мы показали, введением в формулу кулоновской силы и напряженности безразмерной величины - относительной диэлектрической проницаемости среды. Поэтому целесообразно для характеристики электрического поля ввести новую величину, которая не зависела бы от среды, а определялась бы только величиной и распределением электрических зарядов.

Такому условию для изотропной среды удовлетворяет вектор

(9.1.1)

Этот вектор называется вектором электрического смещения (индукции) электрического поля. Для поля точечного заряда в соответствии с формулами (8.3.2) и (9.1.1) величина электрического смещения определяется выражением

(9.1.2)

Единица измерения индукции в СИ - .

При использовании понятия вектора электрического смещения (индукции) электрическое поле также изображается с помощью линий смещения (индукции) аналогично силовым линиям.

Линии смещения (индукции) - это такие линии, касательные к которым в каждой точке поля совпадают с направлением вектора в этой точке.

Картина электрического поля, изображенного с помощью линий смещения (индукции), более простая, чем изображенного с помощью силовых линий. Различие в том, что густота их зависит только от величины заряда, создающего поле, и не зависит от среды.

В вакууме густота линий для и совпадают, в любой другой среде густота линий для в раз больше, чем для (рис. 9.1.1).

Рис. 9.1.1