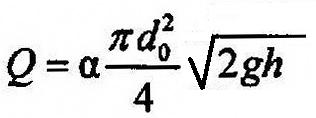- •1.Основные свойства жидкостей и единицы их измерения.
- •3.Основные свойства гидростатического давления.
- •4.Основное дифференциальное уравнение гидростатики.
- •5.Уравнение поверхности уровня и свойства этой поверхности.
- •6.Основное уравнение гидростатики, его геометрическая и энергетическая интерпретации.
- •7.Абсолютное и избыточное давление, приборы измерения давления.
- •8.Эпюра распределения давления несмешивающихся жидкостей.
- •9.Сила давления жидкости на плоские и криволинейные поверхности.
- •10.Закон Архимеда.
- •11.Уравнение распределения давления при равновесии газов в поле силы тяжести.
- •12.Практические приложения основного уравнения гидростатики.
- •13.Основные понятия кинематики жидкости и газа.
- •14.Средняя скорость потока жидкости, способ ее определения.
- •15.Уравнение неразрывности движения капельных и газообразных жидкостей.
- •16.Дифференциальные уравнения движения невязкой и вязкой жидкости.
- •17.Уравнение Бернулли для идеальной жидкости.
- •18.Геометрический и энергетический смысл членов уравнения Бернулли для потока вязкой жидкости.
- •20.Уравнение Бернулли для газов.
- •21.Уравнение Бернулли для неустановившегося движения.
- •22.Принцип работы дроссельных приборов и пневмометрических трубок.
- •23.Уравнение изменения количества движения, его практическое значение.
- •24.Методы определения скорости витания частиц.
- •26.Особенности ламинарного и турбулентного движения жидкости в трубах.
- •27.Физический смысл числа Рейнольдса и его практическое значение.
- •29.Потери напора на трение в круглой трубе при ламинарном режиме движения.
- •30.Способ определения начального участка ламинарного течения.
- •31.Расчет потерь напора на трение в трубах некруглого сечения.
- •32.Понятие о средней скорости при турбулентном режиме движения.
- •33.Влияние шероховатости труб на величину потерь напора на трение.
- •35.Касательное напряжение при турбулентном движении жидкости.
- •36.Основные группы местных потерь напора.
- •37.Факторы, влияющие на потери напора при резком изменении сечения напора потока.
- •38.Потери напора при постепенном изменении сечения потока (конфузор, диффузор).
- •40.Классификация трубопроводов при гидравлическом расчете.
- •41.Основные задачи гидравлического расчета простого трубопровода.
- •42,43.Расчеты длинных трубопроводов в квадратичной области сопротивления с использованием обобщенных гидравлических параметров.
- •44,45.Уравнение расчета длинных трубопроводов в неквадратичной области сопротивления.
- •46.Расчет трубопроводов при последовательном соединении длинных труб.
- •47.Уравнение расчеты сложных трубопроводов при параллельном соединении труб.
- •48.Особенности расчета коротких труб при их последовательном соединении.
- •49.Расчет газопроводов при низких перепадах давления.
- •50.Особенности гидравлического расчета газопроводов высокого давления.
- •51.Влияние срока эксплуатации труб на их гидравлическое сопротивление.
- •52.Гидравлический расчет трубопроводов при движении в них двухфазных жидкостей.
- •53.Факторы, влияющие на величину увеличения давления при прямом и непрямом гидравлическом ударе.
- •54.Классификация отверстий при гидравлическом расчете истечения.
- •55.Причина сжатия струи на выходе из малого отверстия.
- •58.Особенности гидравлического расчета истечения жидкости через большие отверстия.
- •59.Чем отличается насадок от трубопровода.
- •60.Причины изменения расхода и скорости при истечении жидкости через насадки по сравнению с истечением через отверстие.
- •61.Типы насадок, их применение.
- •62.Схема свободной затопленной струи, ее расчет.
- •63.Основные режимы разрушения незатопленной струи.
- •64.Метод определения границ между режимами распада струи жидкости.
- •65.От чего зависит сила давления струи жидкости на твердые поверхности.
- •66.Факторы, определяющие сопротивление тел, находящихся в потоке.
- •67.От чего зависит сопротивление трения при обтекании плоской пластины.
- •68.Влияние режима движения жидкости в пограничном слое на величину коэффициента сопротивления трения.
- •69.Условие образования вихревого течения. Отрыв пограничного слоя.
- •70.Характер распределения давления при обтекании тела потоком жидкости или газа.
- •71.Факторы, определяющие величину силы сопротивления давления.
- •72.Суммарное сопротивление при обтекании твердого тела.
- •73.Что такое скорость витания и гидравлическая крупность.
- •74.Чем обусловлена необходимость использования методов теории подобия?
- •75.Какие явления называются подобными?
- •76.Условия подобия гидравлических явлений.
- •77.Критерии подобия, их свойства и метод получения.
- •78.Формулировка основных теорем подобия.
- •79.Физический смысл основных критериев подобия.
- •1.Критерий Фруда.
- •4. Критерий гомохронности или критерий Струхаля.
20.Уравнение Бернулли для газов.
Уравнении Бернулли в диф. форме имеет вид:
![]()
Для газов, обладающих вязкостью, необходимо учитывать потери энергии на сопротивления:
![]()
Интегрируя это уравнение, получим:
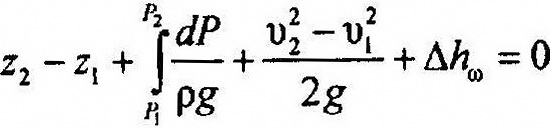
Вид подинтегральной функции зависит от процесса, происходящего при движении газов. Наиболее общим случаем является политропный процесс.
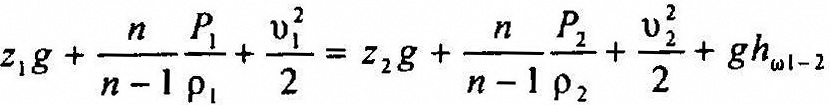
Так как уравнение состояния газов:
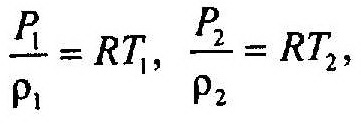 то,
то,
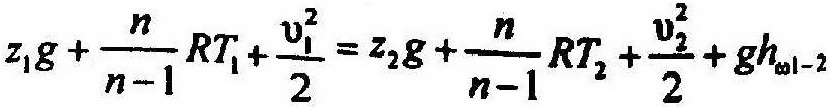
При адиабатическом процессе n=k, поэтому:
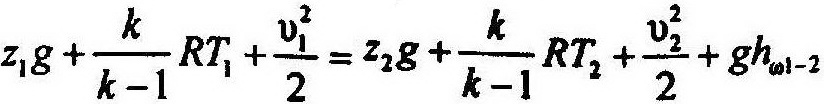
При изотермическом процессе:
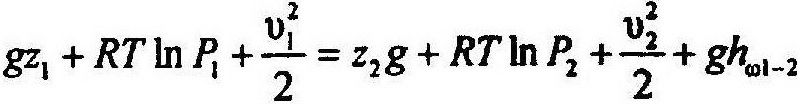
21.Уравнение Бернулли для неустановившегося движения.
Р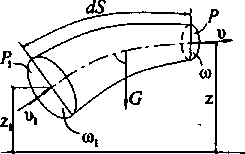 ассмотрим
неустановившийся поток жидкости в
канале, ограниченном
неподвижными стенками. Выберем два
сечения. В первом из них
отметка центра тяжести сечения
z1,
давление Р1,
скорость течения υ1,
в каждый момент времени известны. Второе
сечение выбрано произвольно,
в нем отметка центра тяжести z,
давление Р
и
скорость течения
υ.
По отношению к первому
сечению канала остальные сечения
определяются
криволинейной координатой
S,
совпадающей с осью канала.
ассмотрим
неустановившийся поток жидкости в
канале, ограниченном
неподвижными стенками. Выберем два
сечения. В первом из них
отметка центра тяжести сечения
z1,
давление Р1,
скорость течения υ1,
в каждый момент времени известны. Второе
сечение выбрано произвольно,
в нем отметка центра тяжести z,
давление Р
и
скорость течения
υ.
По отношению к первому
сечению канала остальные сечения
определяются
криволинейной координатой
S,
совпадающей с осью канала.
В любой момент времени распределение давления в канале является функцией координат. Для фиксированного времени для двух сечений можно записать:
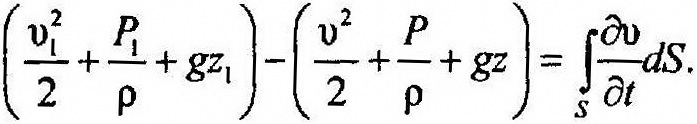
Сумма, представляющая мех. энергию в 1 сечении изменяется во времени. Поэтому и сумма вдоль канала тоже будет изменяться во времени. Изменение мех. энергии м/д 1 и 2 сечением:
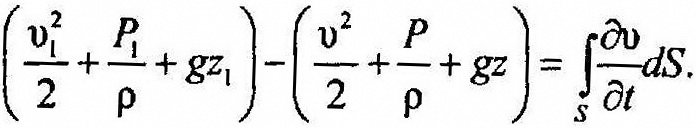
Значение интеграла – затрата мех. энергии на преодоление инерции единицы массы ж. При течении вязкой ж. разность значений мех. энергии должна еще увеличиться за счет гидравлических потерь ΔРω⁄ρ. При течении ж. в трубе постоянного сечения в любой момент времени скорость во всех сечениях одинакова. Это означает:
![]()
В рассматриваемом случае:
![]()
Интеграл наз. инерционным напором, S – криволинейная координата, совпадающая с осью канала.
Т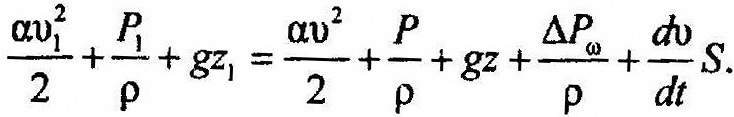 .о.
при неустановившемся течении в трубе
уравнение Бернулли имеет вид:
.о.
при неустановившемся течении в трубе
уравнение Бернулли имеет вид:
Это уравнение сохранения мех. энергии.
Если мех. энергию отнести к 1 веса ж, то:
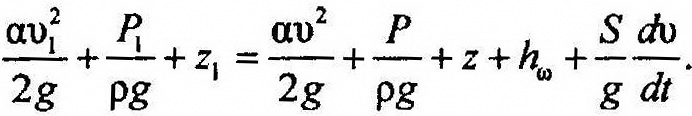
22.Принцип работы дроссельных приборов и пневмометрических трубок.
Для определения скоростей и расходов жидкостей в промышленной практике обычно пригоняются дроссельные приборы и пневмометрические трубки.
П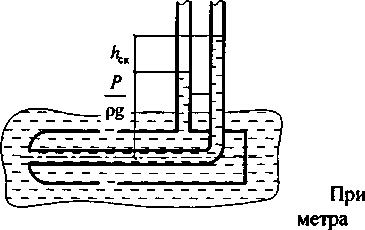 ринцип
работы пневмометрических
трубок
(трубки Пито-Прандтля)
основан на определении пьезометрического
и динамического
напоров. Для этого конец одной трубки
загнут навстречу потоку жидкости в
трубопроводе и уровень жидкости в ней
показывает
сумму пьезометрического и скоростного
напоров. В прямых вертикальных трубках
жидкость поднимается на высоту, отвечающую
гидростатическому
давлению в точках их погружения. Разность
уровней
жидкости в трубках выражает скоростной
напор в точке сечения,
лежащей на оси трубы.
Разность уровней жидкости в трубке
удобнее измерять при помощи дифференциального
манометра. Его U-образная
трубка заполнена рабочей
жидкостью, которая не смешивается с
исследуемой и имеет значительно
большую плотность, например, вода или
спирт - при работе с газами,
или ртуть - при работе с капельными
жидкостями. Это позволяет
измерять значительные перепады давлений
при относительно небольшой высоте
прибора. По результата измерений:
ринцип
работы пневмометрических
трубок
(трубки Пито-Прандтля)
основан на определении пьезометрического
и динамического
напоров. Для этого конец одной трубки
загнут навстречу потоку жидкости в
трубопроводе и уровень жидкости в ней
показывает
сумму пьезометрического и скоростного
напоров. В прямых вертикальных трубках
жидкость поднимается на высоту, отвечающую
гидростатическому
давлению в точках их погружения. Разность
уровней
жидкости в трубках выражает скоростной
напор в точке сечения,
лежащей на оси трубы.
Разность уровней жидкости в трубке
удобнее измерять при помощи дифференциального
манометра. Его U-образная
трубка заполнена рабочей
жидкостью, которая не смешивается с
исследуемой и имеет значительно
большую плотность, например, вода или
спирт - при работе с газами,
или ртуть - при работе с капельными
жидкостями. Это позволяет
измерять значительные перепады давлений
при относительно небольшой высоте
прибора. По результата измерений:
![]() находят максимальную
скорость ж. вдоль оси трубопровода:
находят максимальную
скорость ж. вдоль оси трубопровода:
![]()
Такой способ определения скорости и расхода жидкости прост, но недостаточно точен из-за трудности установки пневмометрических трубок строго вдоль оси трубопровода. Для определения средней скорости жидкости либо снимают эпюру распределения скоростей по сечению трубопровода, передвигая трубку в различные точки сечения, либо используют соотношения м/д средней и мак4симальной скоростями при ламинарном и турбулентном режимах движения. При ламинарном υ=υmax/2. При турбулентном υ=0,8υmax. При движении жидкости в открытом русле устанавливают только пьезометр с загнутым навстречу потоку концом, и высота столба жидкости над свободной поверхностью соответствует скоростному напору. Зная среднюю скорость и площадь сечения находят расход:
Q=υω.
Б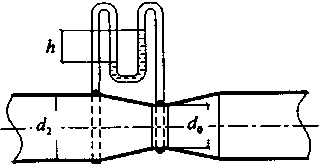 олее
широко распространено определение
скоростей и расходов жидкостей
с помощью дроссельных
приборов, принцип
работы которых основан
на измерении
перепада давлений при изменении
поперечного сечения
трубопровода.
олее
широко распространено определение
скоростей и расходов жидкостей
с помощью дроссельных
приборов, принцип
работы которых основан
на измерении
перепада давлений при изменении
поперечного сечения
трубопровода.
При искусственном сужении сечения потока скорость и, соответственно, кинетическая энергия потока в нем возрастают, что приводит к уменьшению потенциальной энергии давления в этом сечении. Поэтому, измерив дифференциальным манометром перепад давления между сечением трубопровода до его сужения и сечением в самом сужении (или вблизи него), можно вычислить изменение скорости между сечениями, а по нему - скорость и расход жидкости. В качестве дроссельных приборов используют мерные диафрагмы, сопла и трубы Вентури. Мерная диафрагма представляет собой тонкий диск с отверстием круглого сечения, центр которого расположен на оси трубы. Мерное сопло является насадком, имеющим плавный закругленный вход и цилиндрический выход. Труба Вентури имеет постепенно сужающееся сечение, которое затем расширяется до первоначального размера. Вследствие такой формы трубы Вентури потеря давления в ней меньше, чем в диафрагмах или соплах. Вместе с тем длина трубы Вентури очень велика по сравнению с толщиной диафрагмы или сопла, которые могут быть установлены между фланцами трубопровода. Записав уравнение Бернулли для двух сечений потока, выразим скорость υ1 в сечении трубы скорость υ2 - в узком сечении струи за диафрагмой, в которой замеряется давление Р2. Из уравнения неразрывности потока объемный расход жидкости Q в сечении S0 отверстия' диафрагмы (а значит и в трубопроводе) будет равен:
,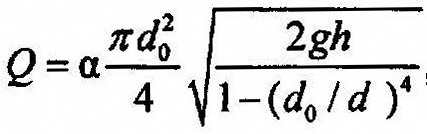 где
α – коэффициент
расхода дроссельного прибора.
где
α – коэффициент
расхода дроссельного прибора.
Диаметр дроссельного устройства обычно в 3-4 раза меньше диаметра трубопровода, а поэтому величиной (d0/d)4 можно пренебречь и находить расход жидкости по уравнению: