Задачі

Задача 1. На ділянці дороги довільної довжини (ділянка А–Н) є вісім споживачів матеріального потоку. Місячний обсяг завезення товарів кожному з них зазначено у дужках. У якому місці треба розташувати розподільний склад?

1)	А	В	С	D	E	F	G	H
	20	10	10	40	10	10	40	50
90=90
2)	А	В	С	D	E	F	G	H
	70	30	10	20	10	60	40	40
140=140

Відповідь: оптимальним місцем для розташування розподільчого складу є: в 1) місце близьке до точки F, 2) місце близьке до точки E або\і F (або між ними), тому, що таким чином відстань до споживачів буде найвигіднішою, і з найменшими витратами.

Задача 2. На території району міста розміщено 5 магазинів одного власника, що торгують продовольчими товарами. Їх координати і місячний товарообіг наведено в таблиці. Знайти координати точок для розміщення оптового складу.

1)	Номер магазину		1. Координата, Х	2. Координата, У	3. Товарообіг, т\місяць
	1		40	60	9
	2		20	100	15
	3		80	70	10
	4		10	82	12
	5		30	15	5
2)	Номер магазину		1. Координата, Х	2. Координата, У	3. Товарообіг, т\місяць
	1		35	100	9
	2		49	15	15
	3		60	25	10
	4		15	60	12
	5		25	70	5

Використаємо формули «Метод центру тяжіння» для визначення координати точок для розміщення оптового складу:

,

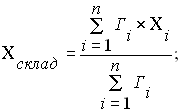
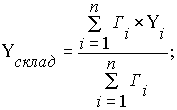де Г_i - вантажооброт i-го споживача;

X_i, Y_i - координати i-го споживача,

n – кількість споживачів.

1)

Х =

_{Y =}

₂₎

Х =

_{Y =}

Відповідь: координати точок для розміщення оптового складу: 1) Х = 33,9 , Y=74,5 ;

2)Х = 38,3 , Y=47,9 .

Задача 3.Власник торгової бази хоче розмістити склад у одному із районів міста, щоб якісно обслуговувати продовольчі магазини. Координати магазинів, транспортні тарифи а також місячний вантажообіг наведено у таблиці. Потрібно знайти координати точок для розміщення оптового складу. При розв’язанні цієї задачі при визначенні координат розміщення складу потрібно враховувати ще і вплив транспортного тарифу.

1)	Номер магазину	Координата, Х	Координата, У	Товарообіг, т\місяць	Транспортний тариф для /-го магазину грн / т. км
	1	40	60	9	0,9
	2	20	100	15	0,75
	3	80	70	10	0,85
	4	10	82	12	0,8
	5	30	15	5	1
2)	Номер магазину	Координата, Х	Координата, У	Товарообіг, т\місяць	Транспортний тариф для /-го магазину грн / т. км
	1	45	45	9	0,9
	2	65	135	15	0,75
	3	75	15	10	0,85
	4	25	35	12	0,8
	5	30	45	5	1

Координати центру ваги вантажних потоків, тобто точки у якій може бути розташовано розподільчий склад, визначається за формулами:

де, Ві – товарообіг і-го споживача; Хі, Yі, - координати і-го споживача; Ті – транспортний тариф для і-го споживача, чи клієнта; n – кількість споживачів.

1)

Х =

Y =

2) Х =

Y =

Відповідь: Координати точок для розміщення оптового складу в заданих системах координат є такими:

1. Хсклад=34,7 ,

Yсклад=72,3 ;

2. Хсклад=50,0 ,

Yсклад=60,6 .

Задача 4. Фірма, що займається реалізацією продукції на ринках збуту KA, KB, KC, має постійних постачальників П1, П2, П3, П4, П5 у різних регіонах. Збільшення обсягу продажів змушує фірму підняти питання про будівництво нового розподільного складу, що забезпечує просування товару на нові ринки та безперебійне постачання своїх клієнтів.

Вихідні дані:

1) тариф для постачальників на перевезення продукції на склад Тп = 1 дол./ т ∙км;

2) тарифи для клієнтів на перевезення продукції зі складу дорівнюють: Тк – KA = 0,8 дол./ т ∙км; KB = 0,5 дол./ т ∙км, KC = 0,6 дол./ т ∙км;

3) ваги вантажів постачальників: Qп – П1 = 150 т, П2 = 75 т, П3 = 125 т, П4 = 100 т, П5 = 150 т.

4) ваги вантажів, що реалізовані клієнтам: Qк – KA = 300 т; KB = 250 т; KC = 150 т.

5) координати клієнтів (RKi) та постачальників (RПi):

Координата	Клієнт			Постачальник
	С1	С2	С3		П1	П2	П3	П4	П5
X	0	300	550		150	275	500	500	600
Y	575	500	600		125	300	275	100	550

Необхідно визначити координати оптимального розташування складу.

Координата	Клієнт			Постачальник
	С1	С2	С3		П1	П2	П3	П4	П5
X	0	300	550		150	275	500	500	600
Y	575	500	600		125	300	275	100	550
Q (обсяг)	300	250	150		150	75	125	100	150
T (тариф)	0,8	0,5	0,6		1	1	1	1	1

Використаємо формулу центру маси або рівноважної системи транспортних витрат:

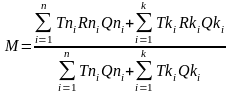, де

М – центр мас, або центр перевізної роботи (ткм);

R_ki – відстань від початку координат до точки, що позначає місце розташування складу клієнта, км;

R_ni – відстань від початку осі координат до точки, що позначає місце розташування складу постачальника, км;

Т_ki – транспортний тариф на перевезення одиниці вантажу клієнта на км, грн./ткм;

Т_пi – транспортний тариф на перевезення одиниці вантажу від постачальника на км, грн./ткм;

Q_ki – вага (об’єм) вантажу, що реалізовується клієнтові i-го складу, т;

Q_ni – вага (об’єм) вантажу, що купується у постачальника i-го складу, т.

Знаходимо параметри:

1. Знаходимо сумарні витрати на транспортування перевезеної партії вантажів від постачальників з урахуванням відстані по осі Х:

∑*T*Q*R=150*150*1+275*75*1+500*125*1+500*100*1+600*150*1=156 375

2. Знаходимо сумарні витрати на транспортування перевезеної партії вантажів від постачальників з урахуванням відстані по осі У:

∑*T*Q*R=125*150*1+300*75*1+275*125*1+100*100*1+550*150*1=168 125

3. Знаходимо сумарні витрати на транспортування перевезеної партії вантажів клієнтам з урахуванням відстаней по осі Х:

_∑*T*Q*R=0*300*0,8+300*250*0,5+550*150*0,6=87 000

4. Знаходимо сумарні витрати на транспортування перевезеної партії вантажів клієнтам з урахуванням відстаней по осі У:

∑*T*Q*R=575*300*0,8+500*250*0,5+600*150*0,6=254 500

5. Знаходимо сумарні транспортні витрати на перевезення для клієнта

∑*T*Q=300*0,8+250*0,5+150*0,6=455

6. Знаходимо сумарні транспортні витрати на перевезення для постачальника

∑*T*Q=150*1+75*1+125*1+100*1+150*1=600

7. Знаходимо координати оптимального місця розташування складу по осі Х:

M=

8. Знаходимо координати оптимального місця розташування складу по осі У:

_M=

_{Відповідь: координати оптимального розташування складу Х=230,7 , У=400,6 .}

5