Вращательные спектры молекул

В газе при значительном разряжении молекулы совершают свободное вращ. движение. Если энергия поступательного движ. молек. принимает любые значения, т.е. меняется непрерывно, энергия вращения принимает лишь строго опред. значения (квантована). Квантомеханическое рассмотрение показывает, что вращат. уровни энергии зависят от вращ. квантового числа и момента инерции. В случае двухатомной молекулы уровни вращат. энергии определяются выражением:

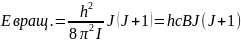
где J - вращательное квантовое число, принимающее положительные целые Значения Ji = 0, 1, 2, 3..; I - момент инерции молекулы: h - универсальная постоянная Планка: B = 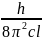вращательная постоянная (см^-1), где с – скорость света

Расположение уровней зависит от индивидуальных свойств молекулы, которые, как следует из уравнения, входят в выражение для момента инерции (массы атомов и расстояния между центром масс и ядрами).

Квантовомеханические правила отбора разрешают переходы между соседними вращательными уровнями, вращательные квантовые числа которых отличаются на единицу. ∆J= ±1. При переходе молекулы с вращательного уровня J на более высокий J + 1 происходит поглощение электромагнитного излучения, энергия которого в точности равна энергии перехода ∆Евращ = 2hcB(J+1). Частота поглощенного света, возбуждении молекулы, определяется по формуле: при возбуждении молекулы, определяется по формуле:

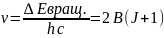
Теперь легко построить систему вращательных уровней и переходов, подчиняющихся требованию ∆J = 1. Вращательный спектр должен состоять в полос поглощения, отстоящих друг от друга на расстоянии 2B (см^-1), что подтверждается экспериментально наблюдаемым вращательным спектром хлористого водорода.

Измеряя расстояние между соседними линиями можно найти момент инерции и межатомное расстояние в молекуле. Момент инерции хлористого водорода относительно главной оси инерции молекулы (I) рассчитывается по формуле:

I =

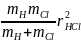
где m_H и m_Cl - массы атомов водорода и хлора; r_HCl - межатомное расстояние.

Колебательные спектры двухатомной молекулы

Простейшая модель колебания двухатомной молекулы рассматривает колебание двух ядер одинаковой массы, связанных упругой пружиной, фазы которого приведены на рис. 39. При сжатии или растяжении пружины возникает сила, стремящаяся вернуть ядра в положение равновесия. Согласно механической модели гармонического осциллятора упругая сила (F) пропорциональна величине смещения ядер от положений равновесия и направлена в сторону, противоположную смешению F= - k∆r. Коэффициент пропорциональности к называется силовой постоянной связи и характеризует жесткость связи.

Малые колебания можно считать гармоническими, и в случае двухатомной молекулы частота колебаний ν_кол связана с приведенной массой (µ) и силовой постоянной выражением: ν_кол = 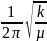, где µ =

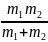
Как видно из формулы (77), частота колебаний возрастает с увеличением жесткости связи и уменьшением массы атомов. Частоты колебаний большинства молекул расположены в инфракрасной области, в диапазоне 400-4000 см^-1.

Квантовомеханическое рассмотрение гармонического осциллятора показывает, что его энергетические уровни определяются выражением:

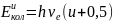
где – энергия колебательного уровня, соответствующая колебательному квантовому числу u, принимающему положительные целые значения u = 0, 1,2,3 и т.д.; 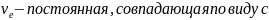ν_кол.

При комнатной температуре большинство молекул находятся в нижнем колебательном состоянии, поскольку средняя энергии теплового движения меньше, чем энергия перехода из основного колебательного состояния п возбужденное kT<h ν_кол.

Поэтому экспериментально легче наблюдать поглощение, соответствующее переходу из основного состояния (u = 0) в первое возбужденное (u = 1). Следует отметить, что при u = 0 Екол.≠0 (Ео = 1/2hν_e) Это значит, что колебания ядер в молекуле никогда не прекращаются, и даже в низшем колебательном состоянии молекула обладает определенным запасом колебательной энергии. При поглощении кванта света v молекула будет переходить на более высокие энергетические уровни. Известно, что энергия поглощенного кванта ранна разности энергий двух состояний, и при ∆u=1:

hv=Eu+1 - Eu = ∆E=hv_e(u+1+1/2)-hv_e (u+1/2) =hv_e

То есть: hv=Eu+1-Eu=hv_e

При сравнении соотношений частота поглощенного излучения (V) равна классической частоте ν_кол.. Таким образом, спектр гармонического осциллятора состоит из одной линии или полосы на частоте V=V_e., являющейся собственной частотой осциллятора.

Наблюдаемая экспериментально инфракрасная полоса поглощения молекул, находящихся в газовой фазе, имеет сложную структуру, т.к. каждое колебательное состояние изолированной молекулы характеризуется своей системой вращательных подуровней.

Частота колебаний возрастает с увеличением прочности связи (кратности связи) и уменьшением массы атомов. Можно приближенно оценить пределы изменения частот колебаний. Например, для группы С = N составляет 2250 см, для C - N - - 1650 см, а для C - N--1050 см В данном случае изменение частоты обусловлено уменьшением силовой постоянной связи атомов С и N, т.к. масса атомов при этом не изменяется.

При поглощении электромагнитной энергии молекула переходит на следующий колебательный уровень и на вращательные подуровни, причем ∆J=±1. В одном случае возникает, так называемая, R-ветвь, которая расположена относительно центра полосы в более высокочастотной области. в другом - Р-ветвь колебательно-вращательной полосы.

В конденсированных средах вращательная структура колебательных полос отсутствует. В этом случае наблюдается полоса, соответствующая чисто колебательному переходу. Для гармонического осциллятора возможны переходы с изменением квантового числа на единицу, т.е. переходы между соседними уровнями. Причем, в инфракрасной области проявляются лишь спектры поглощения двухатомных молекул с отличным от нуля дипольным моментом, т.к. интенсивность поглощения пропорциональна изменению дипольного момента при изменении межатомного расстояния: I ~ 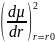, т.е. производной в точке равновесия.

В ИК области проявляются колебания таких молекул, как HCl, HBr, CO, BrCl, LiH. Обычно колебания молекулы бывают в большей или и меньшей степени ангармоничными.

Для ангармонического осциллятора наряду с переходами между соседними уровнями возможны и другие: ∆u = ±1, ±2, ±3 и т.д., что приводит к появлению в спектре удвоенных (2u). утроенных (3u) и т.д. частот колебаний обертонов, интенсивность которых ослабевает. Интенсивность обертонов значительно меньше интенсивности основного тона (∆u = 1). Так, например. интенсивность первого обертона составляет 1-10% ОТ интенсивности основного тона. Интенсивность следующих полос резко убывает, а 3-й, 4-й обертоны для многих молекул наблюдать обычно не удается. По мере роста и расстояние между соседними уровнями сближаются. и при определенном максимальном значении u = Umax энергия молекулы достигает предельного значення Емах. равного энергии диссоциации (Е) за вычетом Е0. т.е. E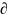 = Emax – Eo.