
Общие представления о строении вещества и физических методах изучения строения.
Вещество и поле – фундаментальные физ. понятия, обозначающих два основных вида материи на макроскопическом уровне.
Вещество – совокупность дискретных образований, облад.массой покоя (атомы, молекулы и все, что из них построено).
Поле – вид материи, хаактериз. непрерывностью и имеющий нулевую массу покоя (ЭМ, гравитационное, квантовое – природное - ядерное).
В ядерном поле участвуют кварки и глеоны. Из них составлены частицы – адроны (бареоны (протоны и нейтроны) и мезоны (р- и к-)). Еще сюда относят гипероны (частицы с быстрым сроком жизни).
m (n0) = 1.674*10-27 кг; m (p+) = 1.672*10-27; m (e̅) ~ -31степень;
Нейтроны могут распадаться на протоны, нейтроны – β-распад.
Вакуум – низшее энергетическое состояние квантового поля, облад. нулевым импульсом, моментом импульса и др. квантовыми числами. Согласно принципу неопределенности в вакууме постоянно рождаются и исчезают виртуальные частицы и происходят нулевые колебания полей.
Строение в-ва – структура отдельных молекул и их соединений, переход из одних структур в другие, их динамич. поведение, связь структ. параметров с физич. химич. биохим. св-вами в-ва, а также законы и положения, управляющие движением вещества и превращением его и матем. аппарат, применяемых для его описания.
Структура в-ва – составная часть его строения. Она определяется для статической формы его части. В газообр. и жидком состоянии значимым часто является молекул. строение в-ва, а в тверд. фазе и для полимеров уже необходимо знать характер взаимод. отдельных молекул или больших сов-тей атомов между собой.
Структура молекулы – состав и расположение наиб. близких ориентированных к друг другу атомов (топология); геометрич. располож. атомов в молекуле – длины связей, углы; распределение эд. плотности и энергии в молек.
Состояния:
Газовое (идеальные, реальные газы)
Жидкое (идеал., реальн. р-ры, коллоиды, гели, расплавы)
Жидко-кристаллическое (мезофаза – нематики (оптически одноосные жидкие кристаллы, имеют дальний ориентационный порядок, смектики – упоряд. двумерный кристалл, имеют слоистую структуру, холестерики, плазама)
Твердое (кристаллы, поликристаллы, композиты, сеталы)
Для изучения структуры в-в используют физические, химические, биохимич. методы. Физическиеоснованы на взаим-ях в-ва и поля: 1. Оптические (рефрактометрия, призменные спектр. приборы, оптич. полиреметрия).
2. Спектральные (спектропоглощ. в УФ, видимой и ИК-областях, эмиссионные спектры излучения в УФ-областях, рентгеновский, флуоресцентный анализ), колебания рассеянния (КР), люминесц. анализ)
3. Масс-спектрометрический
4. Резонансные методы (ЯМР, ЭПР)
5. Фотоэлектронные
6.Рентгенограф. дефракционные
7. Электр. и рентгеновская микроскопия
Спектр. анализ – физич. метод анализа состава вещества, основанный на получении спектра поглощения и излучения ЭМ-волн в различ. диапазонах.
Химические методы основаны на анализе состава исходных веществ и продуктов р-ции, сопоставлений их свойств со свойствами, близких по составу и строению др. в-в.
ЭМ-волны и их свойства
ЭМ-волны – распр.в пространстве переменное ЭМ поле. Явл. поперечными, т.е. векторы Е и Н взаимно перпендикулярны.
rot
E̅ =
 ; rot H̅ =
; rot H̅ =

В случае однородных изотропной непровод. среды, не облад. ферромагнит. или сегнетоэл. св-вами, можно связывать векторным соотношением:
D̅
= ɛɛ0E̅
=> rot
E̅
=

B̅
= μμ0H̅
=> rot
H̅
= ɛɛ0

ɛ0 и μ0 – константы в справочнике
ɛ и μ – относит. диэлектр. и магнитн. проницаемость среды.
Из этого получаем волновое уравнение -
ΔE̅
= ɛμɛ0μ0 ;
ΔН̅ = ɛμɛ0μ0
;
ΔН̅ = ɛμɛ0μ0
Скорость
распр-ия ЭМ-волны: ΔS
=
 ; S
– смещение частиц среды
; S
– смещение частиц среды
v
=
 ; v
– фазовая скорость распространения
волны
; v
– фазовая скорость распространения
волны
c
=
 ; с – скорость света
; с – скорость света
Абсолютный
показатель преломления среды: n
=
 (из-за дисперсии зависит от длины волны)
(из-за дисперсии зависит от длины волны)
Методы определения n: - метод призмы; - рефрактометрический; - интерфериметрический
ЭМ-волна называется плоской, если векторы E̅ и H̅ зависят только от одной координаты Х и от времени (Ex=0; Hx=0)

 Hz
=
Hz
=

 Hy
= -
Hy
= -

 H0
H0
 = E0
= E0

Уравнение плоской волны монохромного света, кот. располагается вдоль ОХ:
Ey
= E0
* Cos (wt – kx +

Hz = H0 * Cos (wt – kx +
k̅
=
 n̅
(n̅
- единичный вектор нормали); v
= λν
n̅
(n̅
- единичный вектор нормали); v
= λν
Величину, обратную длиневолны называют волновым числом
Плотность
потока энергии ЭМ-волны: p
=

Плотность потока связана с объемной плотностью энергии: р = vw
 ;
р̅ = [H̅E̅]
– вектор Умова-Пойтинга
;
р̅ = [H̅E̅]
– вектор Умова-Пойтинга
I
=
 – интенсивность ЭМ-волны
– интенсивность ЭМ-волны
I
=

Для
плоской ЭМ-волны: I
=
 [Вт/м2];
I
= I0*Cos2α
для естеств. света I0
[Вт/м2];
I
= I0*Cos2α
для естеств. света I0

Оптически активная среда – это в-во, вращающее плоскость поляризации плоскополяризованного света по мере прохождения через вещество. Для кристаллических тел угол поворота плоскости поляризации пропорционален толщине кристалла, а в растворах угол поворота пропорционален толщине слоя раствора.
 ;
α – удельное вращение; l
– толщина слоя р-ра; с – конц-ция
;
α – удельное вращение; l
– толщина слоя р-ра; с – конц-ция
Степень
поляризации (P):
Р =
 Р=0 для естественного света и света с
круговой поляризацией.
Р=0 для естественного света и света с
круговой поляризацией.
Для плоскополяризованного света Р=1
Оптич. плотность для частично поляризованного света или для света с эллиптич. поляризацией степень поляризации лежит в пределах от 0 до 1: 0<P<1.
Оптически активные в-ва по разному вращают плоскости поляризации в области элктр. полос поглощения. Зависимость удельного вращения α от λ наз. кривой дисперсии оптич. вращения.
Основной закон светопоглощения Бугера-Ламберта-Бера:
Поглощение света – ослабление светового потока при прохождении через среду ЭМ вследствие перехода энергии вследствие ЭМ во внутреннюю энергию в-ва в рез-те безизлучательных переходов. Наряду с пглощением световых волн наблюдаются процессы рассеяния света, когда ослабление светового потока происходи в результате изменения направления распределения волны, связанное с дифракцией на мелких частицах и флуктуациях на концентрации.
Для оптич. и микроволновых спектров имеется общий з-н поглощения ЭМ-волн, устанавливает связь между величиной интенсивности It и конц-цией поглощающего в-ва. It = I0 – dI
dI согласно з-на Б-Л пропорционален толщине слоя dx. З-н Бера – dI пропорционален числу поглощенных частиц в слое dx (т.е. пропорционален их концентрации).
 ;
С- конц. поглощающих центров (моль/л);
;
С- конц. поглощающих центров (моль/л);
 - коэф. поглощения
- коэф. поглощения
 ;
;
 ;
;
It
=Io
 ; - lg
; - lg
 ;
;
 * 100 = T
* 100 = T
D = - lg T
10-5 – 104 – микроволновые волны
10 нм – 1 мм – оптическое излучение (свет – ИК, видимое, уф-излучение)
10 – 100 нм – рентгеновское излучение (взаимодействие ЭМ заряж. частиц и фотонов с атомами в-ва)
< 0,1 нм – гамма-излучение. Испускаются возбужденными атомными ядрами. При радиактивных превращениях, ядерных реакциях. Могут возникать при распаде частиц. Физические модели строения атомов. Правила квантования, энергии и момента импульса электронов в атомах.
В атоме заряд ядра равен суммарному заряду электронов.
Модели атомов - первая модель Томсона. Вторая - модель Резерфорда, третья - оболочечная квантовая модель (в основу квантовой механ. модели положена квантовая теория атома, согласно которой электрон обладает как свойствами частицы, так и свойствами вещества. Согласно этой теории электроны, в процессе своего движения в атоме образуют электронное облако, вращающийся вокруг ядра электрон движется в определённой области пространства, являющийся наиболее выгодным энергетически. Такая область пространства наз. орбиталью). Простейшая атомная система - атом Н (состоящ. из 1 электрона, движущийся в кулоновском поле одного протона). Водородоподобными или изоэлектронными водороду (имеющим по 1 электрону) явл. ионы Не+, Li++, Be+++.
Спектр атома Н - линейчатый. Частоты, линий этого спектра описываются формулой Бальмера-Ритберга:

Группа линий с одинаковым n наз. серией. Если n=1 серия Лаймера (лежит в УФ обл) , n=2 Бальмера (видимая обл) , 3 - Пашена, 4 - Брекета, 5 - Пфунда, 6 - Хемфри. С 3 и выше - ИК область.
Для изоэлектронных водороду ионов справедливо сериальная ф-ла Бальмера-Ритберга:

Наименьшей частоте для каждого n в формуле Бальмера, при m=бесконечности соответствует границам серии, а частота, соответств. границе серии наз. термой (Тn =R/n^2).
Терм для изоэл. Н иона: Тn=z2R\n2
Соответствующая
терму энергия водородного иона: En
= - ;
Tn
=
;
Tn
=

Абсолютная величина Еn наз. энергия связи электрона в атоме.
Постулаты Бора.
Существуют некот. стационар. состояния атомов, находясь в котором он не излечает энергию. Стационарным состояниям соответствуют стацион. орбиты, при движении по которым электрон не излучает ЭМ - волн.
В стационарном состоянии атома электрон двигаясь по круговой орбите должен иметь квантовые значения момента импульса, удовлетворяющие условию: munrn =

Атом излучает или поглощает квант ЭМ-энергии, когда электрон переходит с орбиты с большим (или меньшим) на орбиту с меньшим или большем n:
hν
= Em
– En
( )
)
Понятие эл. орбиты в атоме явл. условным, вследствие волновой природы электрона в соотношении Гейзенберга. Электроны в атоме представл. в виде заряж. облаков, плотность которых максимальна, на каких то расстояниях r, называемых радиусами орбит.
Среднее
расстояние электрона от ядра в
водородно-подобной системе при z>1 для
квант. чисел n и l: r
=
 a0=0,529*10-8
м
a0=0,529*10-8
м
Орбиты
с l=1,2,3…..проникая в область пространства,
где проходят орбиты электронов заполненных
оболочек, испытывают доп. взаимодействия
с орбитами атомного остатка. Энергетические
уровни Enl атомов с одним внешним электроном
вычисляют по формуле: Enl
= -
z* = z-σ – постоянная экранирования
Квантование проекции момента импульса.
Lz =mh. M=+-1 и тд +-l
Момент
импульса электрона в атоме квантуется
по формуле: Ll
=
 h
h
Связь орбитального момента с магнитным моментом: L0=mvr
Pm=I*S=Inr2
Pm
=
 ;
;
 =
=

Собственный момент импульса
hs
=
 *h
L3z
= Sh
*h
L3z
= Sh
Простейшие оптические методы анализа вещества
Законы отражения и преломления ЭМ волн.
ЭМ - волна, падая на границу раздела двух сред частично отражается от поверхности раздела, а частично преломляется, переходя во вторую среду
Плоскость падения - плоскость, проходящая через падающий луч и перпендикуляр к поверхности раздела сред точки падения.
Показатель преломления среды - величина n, равная отношению скорости ЭМ-волны в вакууме С к её фазовой скорости v в среде.
n =
c/v =

Относительный показатель преломления двух сред - величина n21
Для
неферромагнитных сред: n21
=
 , μ=1; n1=c/v1,
n2=c/v2
, μ=1; n1=c/v1,
n2=c/v2
З-н
преломления:


Если свет. волна из оптически более плотной срелы 1 падает на границу раздела с менее плотной средой 2 (n21<1),то при углах падения α ≥ предельному, где sin α пред. = n21, преломленная волна отсутствует. (явление полного внутреннего отражения).
При полном внутреннем отражении ЭМ-поле свет. волны заходит во вторую среду (быстро), убывают амплитуды векторов E и Н. Для получения и исследования спектрального разложения по частотам или длинам волн используют спектральные оптические приборы. Оптическая система спектр. приборов в пространственном разложении состоит из источника света, узкой входной щели, на которой падает исследуемое излучение переднего объектива (колематор) диспергирующего элемента и заднего объектива(камерный). В качестве диспергирующих элементов используют дифракционные решётки, призмы, Эталон фабри Перо.
Призменных спектральных приборов, призмы располагают обычно под углом наименьшего отклонения. Колематор преобразует расходящийся пучок света от входной щели к параллельной. В задней фокальной плоскости преобразуется параллельный пучок лучей в спектральную систему изображений входной щели. В спектрометрах смотрим на интенсивность.
Призменные спектр. приборы
 α –
преломляющий угол призмы
α –
преломляющий угол призмы
Луч
света падает на призму в плоскости
перпендикулярно ее ребрам A,B,С
после преломления отклоняется к основанию
АВ призмы на угол
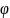

Такое положение призмы относительно источника света наз. установкой под углом наименьш. отклонения.
Ф-ла
призмы: Sin

Угловая
дисперсия призмы: D
=
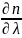 *
*

Разрешающая
способность – 2 близкие спектр. линии,
полученные в спектр. приборе можно еще
считать различимыми, если расстояние
между ними не меньше ширины самих линий.
R
=

Уравнение Шрёдингера: положение частицы в пространстве в данный момент времени определенным заданием волновой функции (вероятность dw того, что частица находится в объеме пропорционально квадрату модуля всей функции).
∂W
~
 2
=
2∂V
2
=
2∂V
 – условие
нормировки, указывает на то, что частица
пребывает где-то в пространстве. Волновая
функция явл. основ. характеристикой
состояния микромолекул – атомов, молекул
и ЭМ-частиц.
– условие
нормировки, указывает на то, что частица
пребывает где-то в пространстве. Волновая
функция явл. основ. характеристикой
состояния микромолекул – атомов, молекул
и ЭМ-частиц.
Ур. Шредингера – основное уравнение, определ. вид функции Ψ для различных случаев движения и взаимодействия микрочастиц.
Гамельтон:
D
=

Ур. Шредингера дополн. условиями, кот. накладыв. на волновую функцию:
1) функция Ψ должна быть конечной, однозадачной и непрерывной
2) Частная производная dΨ по dx; dΨ по dy должны быть непрерывные
3) Тройной интеграл должен быть конечный
Стационарное
ур. Шредингера: ΔΨ+
Строение
многоэлектронных атомов. Особенности
спектр. анализа
Многоэлектронные
атомы имеют сложное строение, кот.
описывается оболочечной моделью и
приближенной квантово механическими
методами. Значение энергии электр.
состояний должно находиться решением
системы из n-уравнений Шредингера. Ур.
имеют вид:
 (E
+
(E
+
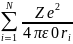 – U)
Ψ = 0
Слагаемое, ответственное за
потенц. энергию взаимодействия е с
ядром
Q - энергия кулоновского взаимод.
электронов между собой.
ri
- расстояние от е до ядра атома.
Нахождение
уровня энергии многоэл. атомов проводилось
эмпирическим путём. С использованием
методов спкктр. анализа и приближ.
расчётов. В общем виде энергия стационарных
состояний е в атомах зависит от значений
4-ех квантов. чисел: n, l, m, s. Электроны с
одинак. знач. n глав. квант. числа образуют
оболочку (n=1,2,3 и тд), тогда число е в
оболочке равно N=2n2
Табл.
– U)
Ψ = 0
Слагаемое, ответственное за
потенц. энергию взаимодействия е с
ядром
Q - энергия кулоновского взаимод.
электронов между собой.
ri
- расстояние от е до ядра атома.
Нахождение
уровня энергии многоэл. атомов проводилось
эмпирическим путём. С использованием
методов спкктр. анализа и приближ.
расчётов. В общем виде энергия стационарных
состояний е в атомах зависит от значений
4-ех квантов. чисел: n, l, m, s. Электроны с
одинак. знач. n глав. квант. числа образуют
оболочку (n=1,2,3 и тд), тогда число е в
оболочке равно N=2n2
Табл.
Название оболочки |
k |
l |
m |
n |
o |
p |
q |
N |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Число электронов |
2 |
8 |
18 |
32 |
50 |
72 |
98 |
В каждой оболочке е распределены по подоболочкам, кот. соответствуют опр. значениям орбит. квант. числа l. Орбит. число квантует момент импульса е в атоме. Все е в атоме делят на внешние и внутренние. Внешние е входят в состав оболочки с наиб. знач. n и приним. участие в образов. химич. связей. Они определяют многие оптические, спектроскопические и др. св-ва вещества. Остальные е oтносятся к внутр. и представ. собой стабильные замкнутые системы. Число е в подоболочке 2*(2l+1). Если рассмотреть процесс формиров. электр. оболочек начиная с атомов Н, то сначала заполняются состояния с наим. возмож. энергией, а затем с более высокой. Для легких атомов это соответствует тому, что сначала заполняется оболочка с меньшим значением n, а потом начинается заполнение след. оболочки с последов. состоянием l=0, l=1 и тд. В таблице Менделеева приведено заполнение оболочек до 34 элемента. Нарушения последовательности заполнения 3d-обрлочки для атом K и Ca обуслов. тем, что энергия 3d-состояния оказывается выше, чем для состояния 4s => она начинает запол. раньше. Если спиновые и орбит. моменты е в подоболочках оказались скомпенсированными, то соответств. элемент облад. диамагнитными св-вами. В атомах с незаполн. подоболочками нескомпенсированный магнит. момент внешних е-нов обуславливает парамагнитные св-ва в-ва. А в ряде случаев ферро- и антиферромагнит. св-ва. Векторная модель строения эл. оболочек и правила отбора для эл. переходов
Для систематизации сложных спектров излучения и поглощения многоэлектр. атомов и изучения тонкой структуры спектров применяется вектор. модель. В ней момент импульса соответствующих орбит. движ. е-нов обозначается l (вектор), а спин е - вектором s. Проекции этих вектров lz = mh (m = 0….l) Sz =s*h (s=½) Сумма векторов дает полный вектор моментов импульса е-нов G В многоэлектр. атоме орбитальные и спиновые моменты всех е-нов могут складываться 2-мя способами: первый - случай слабой связи орбит. и спинового момента е). Общий механич. момент электр. внешней оболочки I = α + S Суммарное квант. число - Второй способ сложения орб. и кв. числа (случай сильной спин-орбит связи) заключ. в том, что сначала складываются моменты для одного электрона, давая вектор полного момента). Мультиплетность - величина 2s+1, которое показывает на какое число компонентов может расщепляться энергетич. уровень, вследствие спинового взаимодействия. В соответствии с 2-мя значениями для атомов с двумя электронами получается 2 вида Мультиплетов, кот. Могут проявиться в спектрах в виде одиночных или тройных спектров, одиночные - синглеты, тройные - триплеты. Мультиплетность уровней энергии сложных атомов явл. причиной появления тонкой структуры.
Электронно-колебательные спектры
Внешние е, ответственные за оптическин и спектральные свойства атомов образуют хим. связи и устойчивые молекулы. Молекулярные спектры за их вид наз. полосатыми. Полосы в молек. спектрах наблюдаются в ИК, видимом и УФ диапазонах шкалы ЭМ-волн. Близкорасполож. полосы образуют группы полос. У простейших 2-ух атомных молекул наблюдаются несколько групп полос. У многоатомных сложных молекул в видимой и УФ-областях спектра наблюдаютс
я сплошные широкие полосы, испускания или поглощения. Отдельная спектральная линия молек. спектра возникает в результате изменения энергии молекулы. Энергия молекулы Е представляется в виде суммы следующих в первом приближении независимых частей: Е = Епост. + Еэл. + Екол. + Евращ. + Еяд.
Епост. (энергия поступательного движения центра инерции молекулы. Не квантуется!!!)
Еэл. (энергия движения электронов в атомах молекулы)
Екол. (энергия колебательного движения ядер атомов, входящих в молекулу около их равновесных положений)
Евращ. (энергия вращательного движения молекулы как целого)
Еяд. (энергия ядер атомов в молекуле, не квантуется!!!)
По правилу частот Бора частота фотона ν испускаемого молекулой при изменении её энергетического состояния равна: ν = ∆E/h=∆Eэл./h + ∆Eкол./h + ∆Eвращ./h
Возникновение густо расположенных линий, образующих полосы в различных участках спектра объясняется тем, что эти изменения энергии находятся в связи: dEэл. » dEкол. » dEвращ. (приближение Борна-Оппенгеймера) :
Заключается в том, что в системе выделяют и раздельно описывают ядра атомов и электроны, для кот. характерные времена изменения состояния сильно различаются. Таким образом, каждый электронный уровень энергии обладает системой энергии подуровней колебательных и вращательных движений. Колебательные и вращ. движения квантуются.
