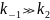Квазиравновесное приближение

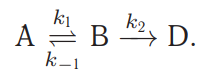
Квазиравновесное приближение применяют в том случае, когда равновесие в обратимой реакции быстро устанавливается и медленно нарушается. Для приведенной выше схемы это означает, что k2 k−1. Между собой конкурируют не процессы образования и расходования интермедиата, как при установлении квазистационарного режима, а два превращения интермедиата, одно из которых ведет к установлению равновесия, а другое — к образованию продукта реакции. Значение константы скорости k1 практически не влияет на применимость данного приближения (рис. 22.2), от него зависит только время установления квазиравновесия.

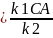k2<<k1: Kравн = k1/k2 =CB/CA → CB → rD= k3CB=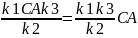

Константы скорости образования вещества Д являются комбинацией из 3-х констант отдельных стадий. Анализ применимости рассмотренных приближений показывает, что в некотором смысле они противоположны друг другу, т.е. квазистационарное приближение, применяется тогда, когда промежуточное вещество распадается быстро, а квазиравновесное, когда медленно.

НЕ НАШЛА КУСОК КАТАЛИЗА, НО БУДЕТ С РОСТОВЦЕВЫМ!!!!!!!!!

Кинетика ферментативных хим. р-ий
Простейшая схема ферментат. катализа Михаэл.-Ментена:
E+S↔(k₁,k_-1) [ES]→(k₂) P+E
В стационарном состоянии(когда субстр. комплекса образуется столько же, сколько и расходуется): r_обр[ES]= r_расп[ES] ; r_обр[ES]=k₁[E]_равн[S] ; rраспада=k₂[ES]+k_-1[ES]
[E₀]исходная конц. фермента=[Eравн]+[ES]
rобр=k₁*([E₀]-[ES])*[S] rрасп=k₂*[ES]+k_-1[ES]
тогда уравнение М-М: rобр=rрасп→k1([E0]-[ES])[S]=k2[ES]+k-1[ES]
[S]k1[E0]-k1[ES][S]=k2[ES]+k-1[ES] ; [S]k1[E0]-k1[ES][S]=(k2+k-1)[ES] ;
[S][E0]-[ES][S]=((k2+k-1)/k1)*[ES]
В квазистационарном состоянии (k2<<k-1) конст. скор. образ. продукта много меньше, чем константа скорости распада комплекса:k2 можно пренебречь (по условию)
k_-1/k₁=Kм →[ES]=([E0][S])/(Kм+[S])
Скорость образования продукта (Р) равна скорости образования фермент-субстратного комплекса [ES], а это: rобр=k2[ES], тогда получаем ур. М: rобр.р=(k2[E0][S])/(Kм+[S])-зависимость rобатной р-ии от концентрации субстрата.
→rобр.р=k2[ES]
конц. [S] при которой скорость р-ии равна ½ max.
Для большинства субстратов Км имеется в литературе, но Км кроме природы фермента и субстрата может зависеть от степени очистки, мобилизации фермента.
Физический смысл: сколько молекул субстрата подвергается превращению 1 молекулой фермента за 1 секунду. k2-число оборотов фермента.
Особенности ферментов как cat:1. Селективность (избирательность) сродство к субстрату или же способность катализировать какую то одну р-ю (один класс ферментов) в смеси;2. Оптимум рН и оптимум Т;3. Строение активного центра;4. Ферменты ускоряют р-ю в большее число раз, чем обычные cat;5. Работают в мягких условиях

Классификация ферментов:
Оксидоредуктазы: р-ии: перенос атомов водорода или е от одного в-ва к другому(дегидрогеназа, оксидаза);Трансферазы: р-ии: перенос определенной группы атомов метильной, ацильной, фосфатной или аминогруппы-одного в-ва к другому(трансаминаза, киназа);Гидролазы:р-ии: реакции гидролиза(липаза, амилаза, пептидаза);Лиазы: р-ии: негидролитическое присоединение к субстрату или отщепление от него группы атомов; при этом могут разрываться связи С-С, C-N, C-O или C-S (декарбоксилаза, фумараза, альдоза);Изомеразы:р-ии: внутримолекулярная перестройка (изомераза, мутаза);Лигазы: р-ии: соедин. 2х молекул в результате образования новых связей, сопряженное с распадом АТФ (синтетаза).
В ур Михаэлиса входит 2 константы: субстратах (Михаэлиса) и число оборотов фермента. В некоторых случаях удобнее пользоваться связанной с числом оборотов другой константой- максимальная скорость: r=(rmax[S])/(Kм+[S])
Должны знать r реакции при различных концентрациях s тогда:
(Лайнуивер-Берг) - недостатки данного способа обработки должно быть 6-7 значений; большая погрешность, так как сначала находится -1/Km а потом Km; 1/r=(Kм+[S])/(rmax*[S]) ; 1/r=(Kм+[S])/(rmax*[S])+1/rmax ; y=kx+b, k=Kм/rmax, x=1/[S], y=1/r, b=1/rmax, tg=Kм/rmax;

r=f(r/[S]): (Иди-Хофсти) y=kx+b, k=-Kм, x=r/[S], y=r, b=rmax, -tg=Kм; вывод: r=(rmax*[S])/(Kм+[S]) /*Kм+[S] r(Kм+[S])=rmax*[S];r*Kм+r*[S]=rmax*[S]/:[S] ((r*Kм)/[S])+r=rmax r=rmax-((r*Kм)/[S]) Достоинства: rmax и Kм находятся сразу.

Ингибирование ферментов-прооцесс, приводящ. к замещению р-ий. Ингибиторы делятся на несколько гр.: 1. Конкурентные-по механизму он блокирует активный центр фермента и работает вместо молекул субстрата (когда близок по св-вам к субстрату) и тем самым снижает число доступных центров для субстрата. Простейшая кинетическая схема р-ии: E+S 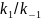[ES] →(k2) P+E фермент связывается обратимо с ингибитором при наличии конкурентного ингибирования: Е+I↔[EI] ; К1=[EI]/([E]*[I]). Решить можно, если применить квазистационарное приближение к комплексу [ES] и квазистационарное к комплексу фермент с ингибитором [EI] с учетом материального баланса по ферменту: [E]₀=[E]+[ES]+[EI] → r=(rmax*[S])/(Kм эфф.+[S]), Kм эфф. зависит от К₁ (влияния комплекса), [I] : Kм эфф.=Км*(1+([I]/K₁), K₁ –константа ингибирования.

: ингибитрованная р-я(rmax остается неизменной); физ.смысл Км: такая концентрация субстрата, при которой r ферментативной р-ии составляет ½ от максимального значения. При увеличении конц. субстрата происходит смещение равновесия; Км эфф. выросла по сравнению с Км; При увеличении конц. субстрата происходит (увеличение конц [ES]) тем больше он будет вытеснять I из активного центра.
2. Неконкурентное ингибирование: E+S [ES]→P+E; Ингибитор связывается с ферментом с фермент-субстратным комплексом!
E+I↔[EI]; К₁=[Ei]/[E][I] ; [ES]+I↔[ESI]; K₁=[ESI]/[ES][I] → r=(rmax эфф*[S])/(Kм+[S]) ; rmax эфф=rmax/(1+([I]/K₁))
Kм-не изменяется, rmax-изменяется

3. Также иногда наблюдается самый сложный тип ингибирования-смешанный.

Теории химической кинетики

Теория элементарной газофазной р-ции. Теория активных соударений.

k = 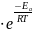; Е_а ~ 0

Согласно этой теории хим. р-ция происходит при каждом столкновении реагир. частиц, соответствующим образом ориентированных относительно друг друга и обладающих энергией, равной (или большей) энергии активации. Чтобы произошла реакция, частицы в момент столкновения должны обладать некоторым минимальным избытком энергии, называемым энергией активации.

В теории активных столкновений считается, что акт превращения начальных веществ в конечные продукты совершается в момент столкновения активных молекул и протекает мгновенно. При этом молекулы рассматриваются как бесструктурные частицы, хотя в действительности химические реакции происходят путем постепенной перестройки молекул и перераспределения энергии между химическими связями.

Средняя арифметическая скорость: =

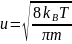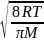
k_B = 1,38*10^-23 Дж/К = 1,596*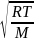

(u₁₂)² = (u₁)² + (u₂)² = ; ;

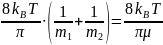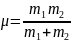u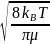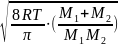₁₂ = = ; d₁₂ =

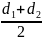
u = πd²₁₂ * u₁₂

z (частота соударений) = πd²₁₂ * u₁₂ * N₂/u

z₁₂ = 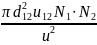= 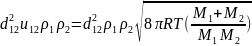; [м^-3 * с^-1]

M₁ = M₂ = M;

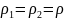
(u₁₁)² = (u₁)² + (u₁)² = 2(u₁)²

(u₁₁)² = 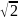(u₁)

z₁₂ = ;

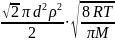Уравнение Трауса-Льюиса:

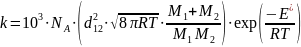
Стерический фактор.

r = P*z*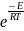

P = 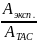1*10^-8

0,01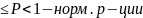 , а если P 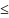0,01 – медленные р-ции

A_эксп. = Р*А_TAC

Разновидности соударений.

d_AB < d_XB <

d_XB – диаметр хим. взаимод.

𝜏 – 10^-12 с ; Т_колеб. = 10^-14 с; 𝜏_{между соуд}. = 10^-10 с

Механизм «мономолекулярной» р-ции в теории активных соударений

Формальная кинетика предполагает, что порядок реакции зависит от молекулярности самой медленной стадии. Согласно теории активных столкновений химическая реакция начинается с соударения двух (значительно реже - трех) молекул. Так как большая часть реакций имеет первый порядок, то это означает, что реакция не ограничивается только столкновением двух частиц.

A 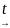B + C

1. p_A – парциальное давление

p_A – больших r не зависит от p_A0

2. p_A – низкие n=1 n=2

3. Инертный газ, не участв. в р-ции в области более низких p_A

Механизм реакции, объясняющий появление первого порядка при столкновении двух молекул, и называется схемой Линдемана.

Е = ½ k_BT; Е_кин. = 3/2kT; Е_кин. = 3/2RT; Т=1000 К; Е_кин. ~ 12,5 кДж/моль

Е_кин << Е_А

A + A 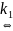A* + A

A* 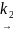продукты

r = k₂[A*]

Принцип квазистационарных концентраций:

;

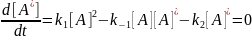
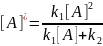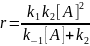
1. Малые p_A:

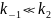
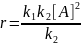= k₁[A]² n=2

2. 

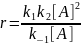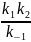= [A]

- эффект. константа

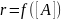
k` =

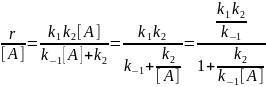
k` =

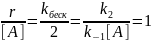
[A] =

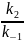
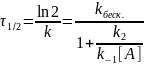
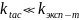
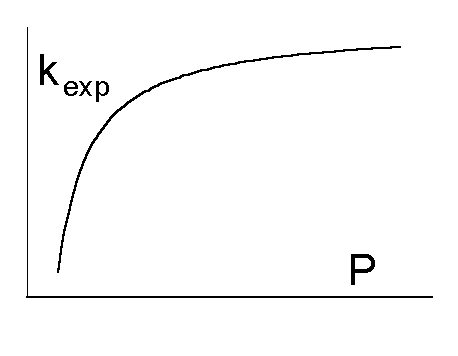
Тримолекулярные р-ции в ТАС

n=3

2NO + X₂ = 2NOX;

k – слабо зависит от t°;

1. 𝜏_соуд. ≠ 0

2. 2 стадии

Еа = 0

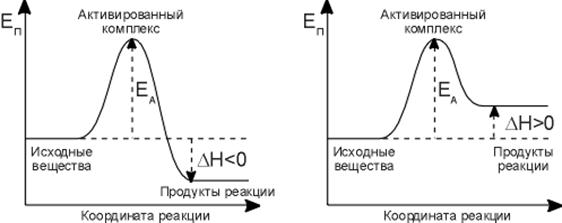
Н + Н + М = Н₂ + М (∆Н<0 – экзотермич.)

1. NO + Cl₂ CO₂

k_c =

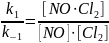
2. NO Cl₂ + NO 2NOCl

[NO Cl₂] = k_c [NO][Cl₂]

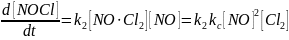
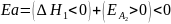
K_эксп. >> K_(TAC)

Теория переходного состояния (ТПС) (активированного комплекса).

Суть теории переходного состояния (активированного комплекса):

1) частицы реагентов при взаимодействии теряют свою кинетическую энергию, которая превращается в потенциальную, и для того чтобы реакция свершилась, необходимо преодолеть некий барьер потенциальной энергии;

2) разница между потенциальной энергией частиц и упомянутым энергетическим барьером и есть энергия активации;

3) переходное состояние находится в равновесии с реагентами;

4) в тех реакциях, где энергия активации существенно ниже энергии разрыва химических связей, процессы образования новых связей и разрушения старых связей могут полностью или частично совпадать по времени.

Время существования активированного комплекса равно периоду колебания одной молекулы ( 10^-13 с), поэтому он не может быть обнаружен экспериментально и, соответственно, его нельзя выделить и изучить.

XY (исх.) + Z X + YZ (продукты)

T = 0 К

Е_пот. = 0 ; Е_колеб. ≠ 0

Е_пот. = hν(u + 1/2); u = 0, 1, 2, 3…

Колеб. число: E0 = Ea – ½*( )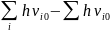

атом + атом: E_a = E₀ +

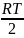
атом + лин. молекула: E_a = E₀ -

2-е линейные молекулы: E_a = E₀ -

2-е нелинейные молекулы: E_a = E₀ -

E0 – Ea > 5 кДж/моль

Термодинамическая версия. Теория переходного состояния.

XY (исх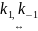.) + Z X-Y-Z 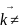X + YZ (продукты)

[X…Y…Z] = C^≠ - конц. молекул в состоянии активир. комплекса.

1. C^≠ << [XY] и [Z]

2. C^≠ - быстро выполняется

k^≠_c = 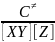; k^≠ - константа скорости мономолекулярного распада АК.

C^≠ - k^≠_c [XY][Z]

r = 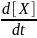= k^≠ = C^≠ = { k^≠ k^≠_c} [XY] [Z]

r = k[XY][Z]

k – константа скорости всей реакции

k = k^≠ * k^≠_c ; k^≠_c = k^≠_p = (

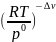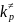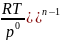
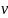∆ – изменение числа молей газообр. веществ.

A + B C; ∆ = -1

n – порядок р-ции

∆_r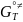 = - RT*ln

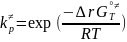
∆_r =

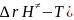
k^≠_c = ( * = ( * *

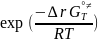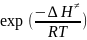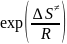
k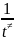^≠ = ; время жизни активированного комплекса

Е_колеб. = k_BT = hν = 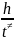= hk^≠ = k_BT => k_B = 1,38 * 10^-23 Дж/К => k^≠ = ;

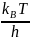Т = 300К; k^≠ = 6,2*10^-12 с^-1

r(k) зависит от с^≠ :

k_c = ( * = ( * *

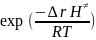Основное уравнение т/д версии ТПС.

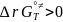, C^≠ << [XY] [Z]

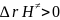k^≠_c << 1

; k^≠_c << 1

Трансмиссионный коэффициент (ꭕ)

В уравнение ТАК следует добавить сомножитель - трансмиссионный коэффициент  . Это небольшая величина, он учитывает скорость обратной реакции, которая может быть больше и меньше единицы. Значения меньшие единицы чаще всего связывают с нарушением условия адиабатичности.

XY (исх.) + Z АК Р1 Р2 Р3

Сравнение ур. т/д версии ТПС с ур. Аррениуса.

k = A*exp (-Ea/RT); А, Еа, ∆Н≠, ∆S≠ - не зависит от t°

ln K = ln A – Ea/RT,

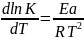
k~T*T^n-1=Tⁿ

ln K~ln Tⁿ = n ln T

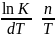
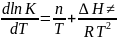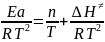; ; Еa = nRT + ∆H≠

Ea = ∆H≠ + 2RT; Ea = ∆H≠ + RT;

lg K = 15,17 - 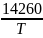(эксп-но)

Предэкспоненциальный множитель. Энтропия активации.

k = A*exp (-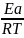 ); k = = =

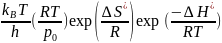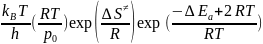
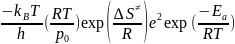
A_эксп. = А_тпс =

Откуда exp: exp(-

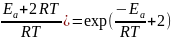
A_эксп. = p*А_тac = p*10³*N_A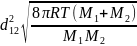

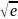
p = 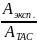= 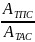; А_ТПС ~ exp

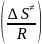
p exp

Мономолекулярные р-ции:

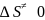
exp

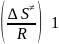
A_ТПС = ( * =

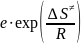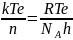
ВЫВОД: Теория активных столкновений основана на подсчете числа столкновений между реагирующими частицами, которые представляются в виде твердых сфер. Предполагается, что столкновение приведет к реакции, если выполняются два условия: 1) поступательная энергия частиц превышает энергию активации E_A; 2) частицы правильно ориентированы в пространстве относительно друг друга. Первое условие вводит в выражение для константы скорости множитель exp(-E_A/RT), который равен доле активных столкновений в общем числе столкновений. Второе условие дает так называемый стерический множитель P - константу, характерную для данной реакции.

В ТАС получены два основных выражения для константы скорости бимолекулярной реакции. Для реакции между разными молекулами (A + B   продукты) константа скорости равна

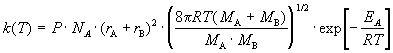
Согласно ТАС, предэкспоненциальный множитель слабо зависит от температуры. Опытная энергия активации E_оп, определяемая по уравнению (4.4), связана с аррениусовской, или истинной энергией активации E_A соотношением:

E_оп = E_A - RT/2.

Мономолекулярные реакции в рамках ТАС описывают с помощью схемы Линдемана (см. задачу 6.4), в которой константу скорости активации k₁ рассчитывают по формулам:

и

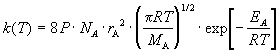
Основное уравнение теории активированного комплекса имеет вид:

Кинетика р-ий в растворах.
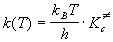
r=f(T, c, природы в-в и растворителя). Группы реакций: 1. Быстрые- скорость лимитируется диффузией(слабо зависят от t и мало чувствительны от природы растворителя). 2. Медленные- когда преодален энергетический барьер (Еа>40 кДж/моль) и должна сформулироваться ориентация частиц.
Молекулярные диффузии (МД). З-ны Фика.
МД-самопроизвольный перенос частиц из области с более высокой в более низкие конц., обусловлены градиентом хим. потенциала: gradμ=
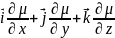
Первый з-н Фика: 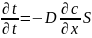, D-коэф. диффузии [м²/с]; n-кол-во в-ва, переносимое за опред. время через некоторую площадку S пропорционально grad конц. и величине поверхности через котор. осущ. перенос.
С1<C2; если идеальный р-р: μ_i=μ₀+RT*lnC_i
если S=1, то j=dn/Sdn диффузионный поток



1-ий з-н:стационарную диффузию описывает(когда постоянная величина описывается); 2-ой з-н: для нестационарной диффузии.
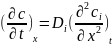, T=const, c_i –f(x,t); зависит от скорости диффузионных процессов; Коэф. диффузии-количеств. хар-ка, зависит от природы в-ва и фазового состояния.
Особенности строения кристаллов и жидкостей. Клеточный эффект.
газы: Ехим→Евзаимод.(взаимод. молекул); ж-тв(крист.): ближний и дальний порядок.
Еколеб=k_BT
Если Т<Tплавл. частицы сущ. в локализованном состоянии и частицы мало подвижны.
кр.→ж: физ. сва-ва меняются незначительно; (при плавлении кристалла возникает резкое повышение конц. вакансии→ж приобретает св-ва текучести→ ж обладает изотропными(одинаковыми) свойствами, которые не зависят от направления), у ж сохраняется только ближний порядок расположения частиц.
ф-ла Стокса: D_A= 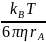[см₂/с] r_A-гидрадинамический радиус дифф. частицы; η-вязкость растворителя; Клеточный эффект-явление, состоящее в ограничении подвижности частиц при дифф. перемещении, обусловл. при налич. ближайшего окружения.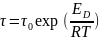
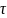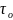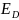, -время пребыв. клетки, -период колебания, -энергия активации диффузии.
D=D₀exp(-E_D/RT), η↑-больше затраты энергии требуется; E_D 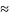ΔHисп/3.
Механизм взаимодействия частиц в «молекулярных клетках»
Классификация р-ий:1. диффузионно контролируемые/быстрые – процесс ограничен только коэф. диффузии D≈1/η; 2. псевдодиффузионные-необходима ориентация частиц Е_А≈0; 3. медленные- скорость не зависит от вязкости растворителя: Е_А>40 кДж/моль.
Диффузионный предел константы скорости р-ии
Ур-е для скорости р-ии: r=kC_АC_В=4π(R_A+R_B)(D_A+D_B)C_AC_B [молекул/м³с²] ;
k_B=r/C_AC_B [м³/моль*с]
k_B=4π10³*N_AR_ABD_AB [л/моль*с] – для расчета диффузионного предела константы скорости р-ии. R_AB=R_A+R_B, D_AB=D_A+D_B
коэф. диффузии: D= 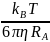ур-е Стокса: D_AB=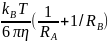
тогда ур-е можно упростить: k_B=4π*10³(R_A+R_B)*(k_BT/6πη)*((1/R_A)+(1/R_B))N_A= *
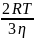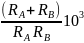
если R_A=R_B, D_A=D_B тогда: k_B=(8RT/3η)*10³
Температурная зависимость: η=η₀exp(B/RT), В(Е-энергия активации вязкого течения)
Чаще всего: kэксп k_D тк Е_А>0(не каждое столкновение приводит к образованию продукта р-ии)