Числовая последовательность. Предел числовой последовательности.

Рассмотрим множество натуральных чисел 1, 2, 3, 4, …..n,…

Пусть каждому натуральному числу по некоторому правилу или закону поставлено в соответствие действительное число х₁, х₂, х₃, … х_n, … Тогда говорят, что на множестве натуральных чисел задана числовая последовательность {x_n}.

Числовая последовательность считается заданной, если указано правило, по которому может быть вычислен любой член последовательности, если только известен его номер. Это правило называется формулой n членапоследовательности.

Например: х_п = n²

Предел последовательности

Число а называется пределомпоследовательности {x_n}, если для всякого ε > 0 найдётся числоN(ε) такое, что для всехn>Nвыполняется неравенство │х_п- а│< ε. Обозначают .

Последовательности имеющие предел называются сходящимися.

Неравенство │х_n-a│< ε равносильно неравенству а – ε < х_n<a+ ε, то есть точки х_n€ (a– ε,a+ ε ) или ε – окрестности точки а. Учитывая это замечание определение предела последовательности можно сформулировать так:

Число а называется пределомпоследовательности, если для любого ε>0 найдется такое числоN(ε), что все члены последовательности с номерамиn>Nпопадут в ε – окрестность точки а. Вне этой окрестности либо не имеется точек х_п, либо имеется конечное их число.

Теорема 1. Если последовательность имеет предел, то он единственный.

Доказательство:

Пусть последовательность имеет два различных предела а и b. Рассмотрим окрестности точек а иbтакой малой величины, что они не пересекаются. Воспользуемся вторым определением предела последо-вательности. Поскольку число а является пределом последовательности, то существует такая окрестность точки а, что все члены последовательности за исключением может быть их конечного числа попадут в ε – окрестность точки а. Так как числоbявляется пределом последовательности, то все члены последовательности за исключением лишь их конечного числа попадут в ε – окрестность точкиb. Таким образом, все члены одного бесконечного множества попали в окрестности двух различных точек, чего быть не может. Получили противоречие. Следовательно, предел единственный и теорема верна.

Основные свойства пределов

Предел алгебраической суммы конечного числа последовательностей равен алгебраической сумме пределов последовательностей слагаемых, если последние пределы существуют.

Предел произведенияконечного числа последовательностей равен произведению пределов последовательностей сомножителей, если последние пределы существуют.

Предел частногопоследовательностей равен частному пределов числителя и знаменателя, если последние пределы существуют и предел последовательности знаменателя отличен от нуля.

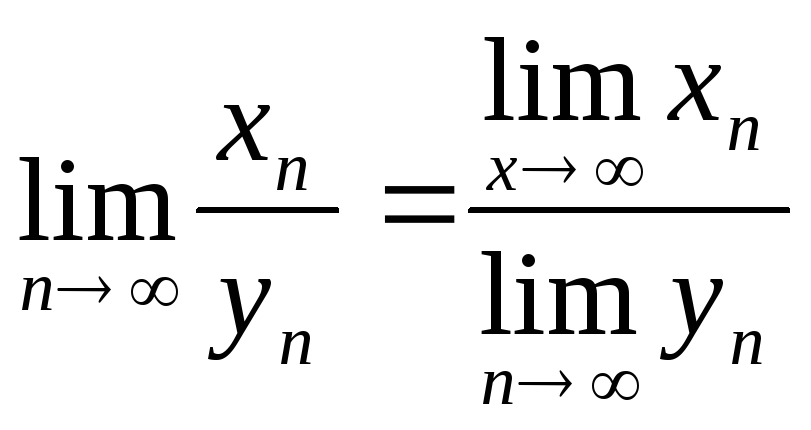
Докажем, например, первое утверждение.

Пусть имеются две последовательности {x_n} и {y_n} и их сумма {x_n +y_n}. Требуется доказать, что

Воспользуемся определением предела последовательности.

Пусть , . Это значит, что для любого ε>0 существует число N, такое что│x_n -a│< и│y_n - b│< .

Составим модуль разности между nчленом последовательности суммы и числом (а+b) и воспользуемся для него свойствами модуля и указанными выше неравенствами.

Будем иметь

│(x_n-y_n ) – (a+b)│= │(x_n–a) + (y_n–b)│<│x_n-a│+│y_n -b│<+=ε

Тогда по определению предела последовательности, утверждение о пределе суммы последовательностей верно.

Аналогично доказываются остальные утверждения.

Предел функции.

Пусть функция определена в некоторой окрестности точкиа за исключением может быть лишь самой точки а. Рассмотрим поведение функции при стремлении аргумента х к значению а.

Определение 1. Число А называется пределом функции при стремлениих к а, если для любой последовательности значений аргументов из области определения функции стремящейся ка, соответствующая последовательность значений функции стремится кА.

Обозначают это так:

Если последовательность значений функции стремится килипри стремлениик значениюа, то говорят, что предел функции равен или.

Обозначают это так:

или

Предел функции при стремленииможно определить по-другому.

Определение 2. Число А называется пределом функции в точкеа, если для , существуеттакое, что для всехх, удовлетворяющих неравенству выполняется неравенство.

Легко доказать, что оба определения предела функции эквивалентны.

Графически определение предела можно представить так:

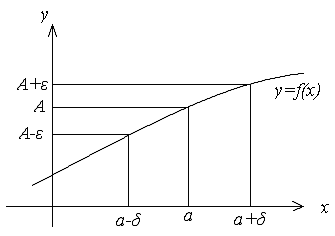
Как только значения аргумента х попадают в –окрестность точкиа, соответствующие значения у попадают в –окрестность точкиА, при этом для существования предела функции при :

1. необязательно, чтобы функция была определена в точке а;

2. –окрестность точки а должна удовлетворять условиям симметричности, а –окрестность точкиА при заданной 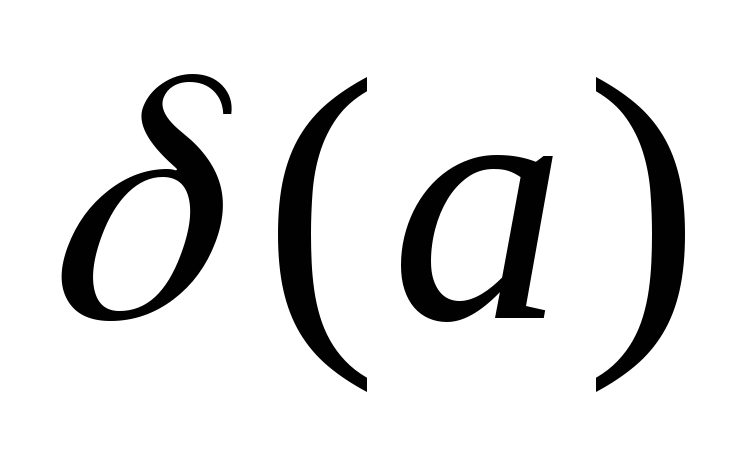не обязательно должна удовлетворять этому требованию.

Определение 3. Число А есть предел функции приесли длясуществует некоторое числоМ такое что неравенство выполняется для всехх удовлетворяющих неравенству