Добавил:

irinattttt Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Технический Университет им. Р.Е. Алексеева

Предмет:

Информатика

Файл:

информатика / 1+2+3 +4+5 лаб работа ручной счет Excel Mcad СИ++

.pdf

Скачиваний:

Добавлен:

28.12.2022

Размер:

2.75 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>

Построение аппроксимирующей функции с помощью команды Поиск решения Формулы

1Данные/Поиск решения

2Целевая ячейка $G$7-минимальное значение

3Изменяемая ячейка $C$2:$E$2

4Выполнить

Результат

Интерполяция

Название метода

Метод

неопределённых

коэффициентов (интерполяция)

Метод неопределённых коэффициентов

Система для нахождения коэффициентов							Ответ
		полинома
полином 1 степени							P1(x)=a0+a1*x
		a	a	x	y
		0	1	0	0
		a	a	x	y
		a	a	x	y
		0	1	1	1
полином 2 степени							P2(x)=a0+a1x+a2x2
a a x a x2						y	P2(x)=a0+a1x+a2x2
a a x a x2						y
	0	1	0	2	0	0
a0 a1 x1 a2 x12 y1
a a x a x2						y
	0	1	2	2	2	2

Ручной счет Интерполяция полином 1 степени.

Зададим общий вид полинома 1 степени P1(x)=a0+a1*x. Выберем для построения 0- ю точку и 3-ю точку. Для нахождения коэффициентов полинома необходимо решить систему линейных уравнений

a0 a1 x0 y0a0 a1 x3 y3

Получаем систему:

		0		0.2	1	0.1
a					a
a			0.85 a			0.9
	0
					1

Запишем систему в матричном виде.

	0,2		a		0,1
1			0
1	0,85			0,9
		a
			1

Решим систему методом Гаусса.
1	0,2 0,1	Перепишем 1- е уравнение без изменений, а из 2-е уравнения вычтем 1-е

1	0,85 0,9

								1		0,2
уравнения и результат запишем на место второго уравнения. Получим систему									0	0,65
						0			0	0,65
						0		1	0,1
					a		0,2a		0,1		.
Запишем полученные данные в виде системы линейных уравнений:						0,65a			0,8		.
						0,65a			0,8
							1
Из 2-го уравнения найдём a				0,8	. Получим a 1,231. Из 1-го уравнения найдём
Из 2-го уравнения найдём a					. Получим a 1,231. Из 1-го уравнения найдём
			1	0,65	1
				0,65
a0 0,1 0,2 a1 .
a0		0,1 0,2 1,231
a0	0,146 .
Запишем найденное уравнение P1(x) 0,146 1,231 x .
Найдём отклонения полученного полиномаP1(x) от заданных точек y.
В 0-ой точке
O0 P1( x0 ) y0
P1(x ) 0,146 1,231 x
		0	0
P1( 0,2 ) 0,1
O		0,1 0,1 0
0
В 1-ой точке
O		P1( x	) y
1		1	1
P1(x ) 0,146 1,231 x
		1	1
P1(0,4) 0,346

0,1
0,8
0,8

O1 0,346 0,5 0,154

В 2-ой точке
O	P1( x		2	) y	2
2			2		2
P1(x		) 0,146 1,231 x				2
	2					2
P1(0,7) 0,715
O2	0,715 0,6 0,115
В 3-ей точке
O	P1( x			) y
3		3		3
P1(x3 ) 0,146 1,231 x3
P1( 0,85) 0,9
O	0,9 0,9 0
3
В 4-ой точке

O4 P1( x4 ) y4

P1(x4 ) 0,146 1,231 x4

P1(1) 1,084

O4 1,085 0,7 0,385

Построим график функции P1( x ) и отметим исходные точки на этом же графике

Интерполяция

1,2

0,8

0,6

0,4

0,2

0,5

1,5

P1(x)

Реализация метода в Mcad

Метод неопределённых коэффициентов(полином 1- ой степени P1(x)=a0 + a1 x)

	0.2					0.	1

		0.4				0.	5
x 0.7				y 0.			6
	0.85					0.	9

		1				0.	7
	1	x		y	0
C		0	D		0

	1	x		y
	1	x		y
		3			3
a C 1 D
	0.146
a
	1.231

Исходные данные

i 0 4

Матрицы C и D для системы линейных уравнений

Решение системы линейных уравнений нахождение коэффициентов а0 и а1

P1(x) a0	a1 x	Интерполирующая функция
		Интерполирующая функция
Вычисление ошибки интерполяции			График найденного полинома и
			исходных точек
Oi P1 xi yi			1.5
Oi			1.5
Oi		y i	1
		y i	1
		P1 xi	0.5
		P1 xi

			0


				0	0.5	1
				0	0.5	1
					xi
					xi

Реализация в программе MS Excel Построение интерполирующей функции с помощью тренда

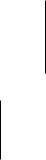
Линейная интерполяция

1.Ввести исходные данные – значения Х разместить в 1- й строке значения Y во второй строке.

2.Построить диаграмму по всем точкам (тип диаграммы – «Точечная»).

3.Для построения полинома 1-й степени P1(x)= a0 +a1·x выберем две точки (x0,

y0) и (x3, y3).

4.Добавим ряд из этих точек.

5.Построим для этого ряда линейный тренд и показать уравнение на диаграмме.

Ручной счет Интерполяция полином 2 степени.

Зададим общий вид полинома 2 степени P2(x)=a0+a1*x+a2*x2. Для нахождения коэффициентов полинома необходимо решить систему линейных уравнений

a		a	x	a	x2		y
	0	1	0	2	0		0
	a	a	x	a	x	2	y

	0	1	1	2	1		1
	a	a	x	a	x	2	y

	0	1	4	2	4		4

Получаем систему:

a			0	0,2 a			0,22		a		2	0,1
			0			1					2
	a			0,4 a			0,4	2	a			0,5
	a	0		0,4 a			0,4		a		2	0,5
		0				1					2
			a			1 a	2			0,7
			a		0	1 a	1 a		2	0,7
					0	1			2

Запишем систему в матричном виде.

111

0,2	0,04	a	0		0,1

0,4	0,16	a		0,5
1			1

	1	a2		0,7

Решим систему методом Гаусса.

1		0,2
	1	0,4


1		1

0,04		0,1

0,16		0,5

1		0,7

Перепишем 1- е уравнение без изменений, а из 2-е уравнения вычтем 1-е

уравнение и результат запишем на место второго уравнения, из 3-го уравнения вычтем 1-е уравнение и результат запишем на место третьего уравнения.

1
1		0,2	0,04	0,1
	0	0,2	0,12	0,4	В результате получаем систему.
	0	0,8	0,96	0,6
	0	0,8	0,96	0,6

. Выполним деление 2-е уравнение на 0,2 , 3-е уравнение на 0,8. В результате получим систему


1			0,2 0,04 0,1
		0	1	0,6 2
		0	1	1,2 0,75	. Перепишем 1-е и 2- е уравнение без изменений, из 3-го

уравнения вычтем 2-е уравнение и результат запишем на место третьего уравнения.
1			0,2 0,04 0,1
	0		1	0,6 2
	0		0
				0,6 1,25

			a	0	0,2a 0,04 a			2	0,1
				0	1			2
Запишем полученные данные в виде системы линейных уравнений:					a1 0,6 a2 2				.
					0,6 a	2	1,25
						2
Из 3-го уравнения найдём a2	1,25	. Получим a2	2,083 .
	0,6

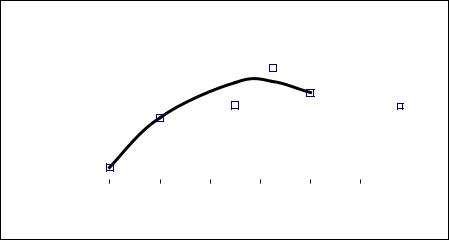
Из 2-го уравнения найдём Из 1-го уравнения найдём

a1 2 0,6 a2 .	a1 2 0,6 ( 2,083)	a1 3,25 .
a0 0,1 0,2 3,25 0,04 ( 2,083) . a0 0,467		. Запишем найденное

уравнение P2(x) 0,467 3,25 x 2,083 x					2	.
уравнение P2(x) 0,467 3,25 x 2,083 x						.
Найдём отклонения полученного полиномаP2(x) от заданных точек y.
В 0-ой точке
O	P2( x	) y		P2(x ) 0,467 3,25 x			2,083 x	2	P2( 0,2 ) 0,1
O	P2( x	) y	0	P2(x ) 0,467 3,25 x			2,083 x		P2( 0,2 ) 0,1
0	0		0	0		0	0

O	0,1 0,1 0
0

В 1-ой точке

O	P2( x	) y
1	1	1

В 2-ой точке

P2(x1 ) 0,467 3,25 x1 2,083 x12

P2( 0,4 ) 0,5

O	0,5 0,5 0
1

O	P2( x		) y		P2(x	) 0,467 3,25 x		2,083 x	2
O	P2( x	2	) y	2	P2(x	) 0,467 3,25 x	2	2,083 x	2
2		2		2	2		2		2
В 3-ей точке
O	P2( x		) y		P2(x ) 0,467 3,25 x			2,083 x	2
3	3		3		3	3		3
O 0,791 0,9 0,109
3

P2(0,7) 0,787	O	0,787 0,6 0,187
	2
P2(0,85) 0,791

В 4-ой точке

O	P2( x	4	) y	4	P2(x	4
4		4		4		4

Построим график функции

) 0,467 3,25 x	4	2,083 x 2	P2(1) 0,7	O	0,7 0,7 0
	4	4		4
P2( x ) и отметим исходные точки на этом же графике.

Интерполяция

1
1
0,9
0,9
0,8
0,8
0,7
0,6							y


0,5							P1(x)
0,5
0,4



0,3
0,3
0,2
0,2
0,1
0,1
0
0
0	0,2	0,4	0,6	0,8	1	1,2

Реализация метода в Mcad

Реализация в программе MS Excel Построение интерполирующей функции с помощью тренда

Квадратичная интерполяция

1.Ввести исходные данные – значения Х разместить в 1- ой строке значения Y во второй строке.

2.Построить диаграмму по всем точкам (тип диаграммы – «Точечная» точки без соединения линиями).

3.Для построения полинома 2-й степени P2(x)= a0 + a1 x + a2 x2 выберем три точки (x0, y0), (x1, y1) и (x4, y4).

4.Добавим ряд из этих точек.

Построим для этого ряда полиномиальный тренд 2-й степени и показать уравнение на диаграмме.

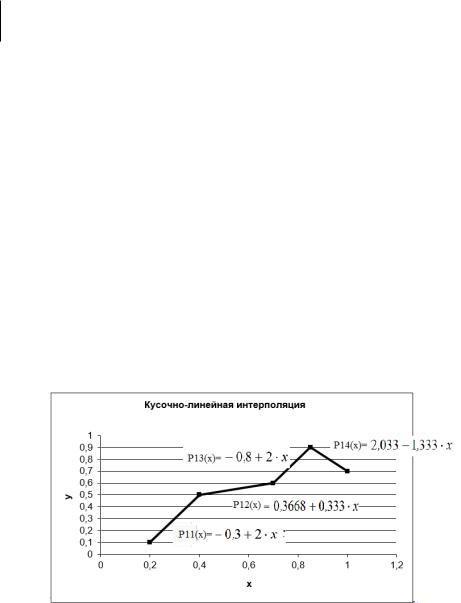
Кусочно-линейная интерполяция (Метод неопределённых коэффициентов)

Постановка задачи: Дана таблично заданная функция {xi,yi}

i	0	1	2	3	4
x	0,2	0,4	0,7	0,85	1
y	0,1	0,5	0,6	0,9	0,7

Выполнить кусочно – линейную интерполяцию.

Система для нахождения

Ответ

коэффициентов полинома на

каждом участке

1 участок

2участок

a1 a1

x,приx

x x

x,приx

x x

P1( x ) a3

x,приx

x x

3 участок

4участок

a40 a41 x,приx3 x x4

a3 a3 x y

На интервале от 0,2 до 1 задано 5 точек, получаем 4 отрезка. Интерполируем (метод Неопределенных коэффициентов) полиномом 1 степени каждый отрезок. После нахождения каждого полинома запишем результат.

1 участок.

								P11( x ) a1 a1 x
i	0	1	Общий вид полинома					P11( x ) a1 a1 x						. По условию интерполяции полином
												0	1
x	0,2	0,4										0	1
x	0,2	0,4	должен проходить через точки, которые выбраны для построения, т.е.
y	0,1	0,5
y	0,1	0,5		P11( x	) y	0						a1	a1 x		y	0
				P11( x	) y							a1	a1 x		y
				0								0	1	0			. Подставим значения
				P11( x	) y		Следовательно					a1	a1 x		y		. Подставим значения
				P11( x	) y							a1	a1 x		y
				1	1				0			0	1	1	1
									0		1	0,2 0,1
x0	,x1, y0 , y1		. В результате получаем						a1	a1		0,2 0,1		.Неизвестными в системе являются
x0	,x1, y0 , y1		. В результате получаем						a1	a1		0,4 0,5		.Неизвестными в системе являются
									a1	a1		0,4 0,5
									0		1
									1		0,2 0,1
a10 ,a11 .Решим систему методом Гаусса.													. Приведем систему к треугольному виду,
									1		0,4 0,5

для этого 1 строку перепишем, из 2 строки вычтем 1 строку и результат запишем на место 2

строки.

1
	0

0,2 0,2

0,1
0,4
0,4

. Запишем полученную матрицу в виде системы.

a1	a1
0		1
a1		0,2
a1		0,2
	1

0,20,4

. Из

2 уравнения найдем a1

0,4

a1 2 . Из 1 уравнения найдем

a1 .

0,1 0,2 a1

0,2

0,1 0,2 2

0,3. Запишем найденное уравнение

P11( x ) 0,3 2 x . Проверка.

Найденное уравнение должно проходить через точки x0 , y0 , x1, y1 .

P11( x

) 0,3 2 x

P11( 0,2 ) 0,3 2 0,2

P11( 0,2 ) 0,1

P11( x

) 0,3 2 x

P11( 0,4 ) 0,3 2 0,4

P11( 0,4 ) 0,5 Следовательно прямая проходит через 0 и 1 точки.

2 участок.

Общий вид полинома P12( x ) a20

a21 x . По условию интерполяции

0,4

0,7

полином должен проходить через точки, которые выбраны для построения, т.е.

0,5

0,6

P12( x

) y

a2 x

Следовательно

1 1

1 . Подставим значения

P12( x2 ) y2

a20

a21 x2

x	,x	2	, y
1		2	1

a2	0	,a2
	0	1

, y2	a20
	. В результате получаем	a2
			0

1 .Решим систему методом Гаусса. 1

a21 a21

0,4 0,7

0,4

0,7

0,5
0,6	.
0,6

	0,5	.Неизвестными в системе являются
	0,6	.Неизвестными в системе являются
	0,6

Приведем систему к треугольному виду,

для этого 1 строку перепишем, из 2 строки вычтем 1 строку, и результат запишем на место 2

1		0,4	0,5						a2			a2 0,4 0,5
									a2			a2 0,4 0,5
											0			1
строки.					. Запишем полученную матрицу в виде системы.						0			1
строки.	0	0,3	0,1		. Запишем полученную матрицу в виде системы.						a2			0,3 0,1
	0	0,3	0,1								a2			0,3 0,1
													1
2 уравнения найдем				a2		0,1	a2	0,333. Из 1 уравнения найдем a2		.	a2		1	0,5 0,4 a
						0,1			0				0

					1	0,3	1
						0,3

. Из

a2	0		0,5

P12( x )
x		, y , x
1			1

0,4 0,333 a2
0,3668 0,333
2	, y	2	.

0 x

0,3668. Запишем найденное уравнение

. Проверка. Найденное уравнение должно проходить через точки

P12( x		) 0,3668 0,333 x
1		1
P12( 0,4 ) 0,3668 0,333 0,4
P12( 0,4 ) 0,5
P12( x	2	) 0,3668 0,333 x	2

P12( 0,7 ) 0,3668 0,333 0,7

P12( 0,7 ) 0,6

3 участок.

Следовательно прямая проходит через 1-ю и 2-ю точки.

i	2	3	Общий вид полинома							P13( x ) a3				a3 x		. По условию интерполяции
													0		1
x	0,7	0,85											0		1
x	0,7	0,85	полином должен проходить через точки, которые выбраны для построения, т.е.
y	0,6	0,9
y	0,6	0,9		P13( x		2	) y	2					a3		a3 x	2	y		2
				P13( x			) y						a3		a3 x		y
														0	1					. Подставим значения
				P13( x			) y		Следовательно				a3		a3 x		y			. Подставим значения
				P13( x			) y						a3		a3 x		y		3
						3	3				0			0	1	3			3
											0	1		0,7 0,6
x2	,x3 , y2 , y3		. В результате получаем								a3	a3		0,7 0,6		.Неизвестными в системе
x2	,x3 , y2 , y3		. В результате получаем								a3	a3	0,85 0,9			.Неизвестными в системе
											a3	a3	0,85 0,9
											0	1
являются a30			,a31											1	0,7 0,6
являются a30			,a31		.Решим систему методом Гаусса.										0,85 0,9			. Приведем систему к
														1	0,85 0,9

треугольному виду, для этого 1 строку перепишем, из 2 строки вычтем 1 строку, и результат

1		0,7 0,6	. Запишем полученную матрицу в виде системы.
запишем на место 2 строки.	0	0,15 0,3

0		1	0,7 0,6
a3	a3
a3		0,15 0,3

	1

. Из 2 уравнения найдем a31 0,3 0,15

a31

. Из 1 уравнения найдем a30 .

a3 0,6 0,7 a3			a3		0,6 0,7 2	a3 0,8	. Запишем найденное уравнение
0		1		0		0
P13( x ) 0,8 2 x . Проверка. Найденное уравнение должно проходить через точки
x2 , y2 , x3 , y3 .
P13( x	2	) 0,8 2 x		2
	2			2
P13( 0,7 ) 0,8 2 0,7
P13( 0,7 ) 0,6

P13( x3 ) 0,8 2 x3

P13( 0,85) 0,8 2 0,85

P13( 0,85) 0,9 .Следовательно, прямая проходит через 2-ю и 3-ю точки.

4 участок.
i	3	4	Общий вид полинома P14( x ) a40 a41 x . По условию интерполяции
x	0,85	1
			полином должен проходить через точки, которые выбраны для построения, т.е.
y	0,9	0,7


	P14( x		) y									a4		0	a4			x	3	y	3
		3	3											0		1			3		3		3		4			3		4
					Следовательно																	. Подставим значения	3	,x	4	, y		3	, y	4	. В
	P14( x		) y		Следовательно						a4				a4			x		y		. Подставим значения	x	,x		, y			, y		. В
	P14( x	4	) y	4							a4			0	a4			x	4	y	4
		4		4			0							0		1			4		4
							0		1		0,85 0,9
результате получаем						a4		a4			0,85 0,9							.Неизвестными в системе являются a4									0			1
результате получаем						a4			a4				1 0,7					.Неизвестными в системе являются a4										,a4
						a4		0	a4				1 0,7
								0			1
.Решим систему методом Гаусса.										1			0,85				0,9		. Приведем систему к треугольному виду, для
										1			0,85				0,9
											1				1		0,7
											1				1		0,7

этого 1 строку перепишем, из 2 строки вычтем 1 строку, и результат запишем на место 2 строки.

1		0,85 0,9		a4		a4		0,85 0,9
					0		1
		0,15 0,2	. Запишем полученную матрицу в виде системы.						. Из 2
	0			a4			0,15 0,2

						1

уравнения найдем a4
		1
a4	0	0,9 0,85 a4
	0	1

уравнение P14( x ) 2

	0,2		a4	1,333. Из 1 уравнения найдем a4		0	.

	0,15		1

a40		0,9 0,85 ( 1,333) a40			2,033. Запишем найденное
,033 1,333 x . Проверка. Найденное уравнение должно проходить через

точки

x	, y	, x	4	, y	4	.
3	3		4		4

P14( x		) 2,033 1,333 x
3		3
P14( 0,85) 2,033 1,333 0,85
P14( 0,85) 0,9
P14( x	4	) 2,033 1,333 x4

P14(1) 2,033 1,333 1

P14(1) 0,7

.Следовательно, прямая проходит через 3-ю и 4-ю точки.

Запишем ответ

		0,3 2 x,если0,2 x 0,4
	0,3668 0,333 x,если0,4 x 0,7
	P1( x )	0,8 2 x,если0,7 x 0,85
		0,8 2 x,если0,7 x 0,85
		2,033 1,333 x,если0,85 x 1
		2,033 1,333 x,если0,85 x 1

Построим график

Реализация метода в Mcad

Метод неопределённых коэффициентов(кусочно-линейная интерполяция)

	0.	2					0.1
	0.	4					0.5
	0.	4					0.5
x	0.	7		y			0.6
	0.85						0.9

	1						0.7
1 участок
	1	x			y	0
C1			0	D1		0

	1	x			y
	1	x			y
			1			1

a1 C1 1 D1

0.3

P11(x) a10 a11 x

2 участок

	1		x		y	1
C2			1	D2

		1	x		y

			2			2

a2 C2 1 D2

0.3670.333

P12(x) a20 a21 x

Исходные данные

i 0 4

Матрицы C1 и D1 для системы линейных уравнений

Решение системы линейных уравнений нахождение коэффициентов а10 и а11

Интерполирующая функция 1 участка

Матрицы C2 и D2 для системы линейных уравнений

Решение системы линейных уравнений нахождение коэффициентов а20 и а21

Интерполирующая функция 2 участка

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>