
информатика / 1+2+3 +4+5 лаб работа ручной счет Excel Mcad СИ++
.pdf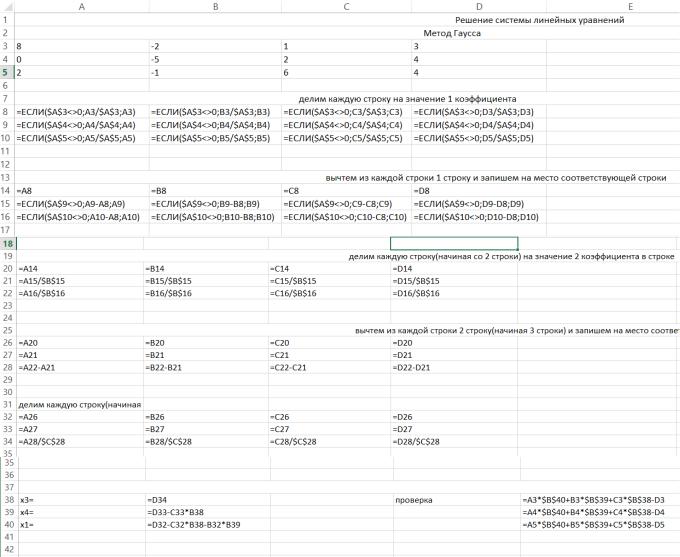
Реализация в Mcad
21


2. Метод Зейделя Постановка задачи: Дана система линейных уравнений
8x1 -2x2 +x3 =3 -5x2 +2x3 =4 2x1 -x2 +6x3 =4
Найти приближенное решение с заданной степенью точности eps=0,1
Ручной счет |
|
|
|
|
8 |
−2 |
1 |
1 |
3 |
Запишем систему в матричном виде [0 |
−5 |
2] [ 2] = [4] (A*x=B) |
||
2 |
−1 |
6 |
3 |
4 |
3.Для того чтобы получить решение с помощью этого метода необходимо чтобы матрица A удовлетворяла следующим требования:
вматрице A абсолютные значения всех диагональных элементов были больше суммы модулей всех остальных элементов в соответствующей строке.
Aii |
Aij |
,что означает |8|>|-2|+|1| |
|8|>|3| |
|-5|>|0|+|2| |
|5|>|2| |
||
|
i 1,i j |
|6|>|2|+|-1| |
|6|>|3| |
|
|
Данное условие называется условием сходимости метода.
4.Если условие сходимости выполнено, то на следующем этапе необходимо задать начальное приближение неизвестных, в качестве которого обычно выбирается нулевые значения:
10 = 0 |
20 = 0 |
30 = 0 |
Верхний индекс - номер итерации (приближения).
3. Формируем циклический процесс, каждый цикл которого представляет собой
23
одну итерацию. В результате каждой итерации получается новое значение неизвестных. Для организации итерационного процесса запишем нашу систему в приведенном виде – из 1-го уравнения выражаем x1, из 2-го уравнения выражаем x2,
из 3-го уравнения выражаем x3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Приведенная система уравнений имеет вид: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
1 = |
3 + 2 2 − 3 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 = |
−4 + 2 3 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{ 3 = |
4 − 2 1 + 2 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
||||
Запишем итерационную формулу метода Зейделя: |
|
|
|
|||||||||||||||||||||
|
|
|
|
1 +1 = |
|
3 + 2 2 |
− 3 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 +1 |
= |
|
−4 + 2 3 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 +1 = |
4 − 2 1 +1 + 2 +1 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
{ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Переходим к вычислению 1-ой итерации: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
i=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 = |
3 + 2 20 − 30 |
3 + 2 0 − 0 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
= 0,38 |
||||||||
|
8 |
|
|
|
|
|
8 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
21 |
|
|
−4 + 2 30 |
|
|
|
|
|
−4 + 2 0 |
|
|
|
|||||||||||
|
= |
|
|
|
|
|
= |
|
|
|
|
|
|
|
= −0,80 |
|
||||||||
|
5 |
|
|
|
|
|
5 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
31 = |
4 − 2 11 + 21 |
= |
4 − 2 0,38 + (−0,80) |
= 0,41 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|||||||||
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Проверим достигнута ли точность: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|x11-x10|<eps |
|0,38-0|<0,1 |
|
|
|
|
|0,38|<0,1 нет |
|
|
|
|||||||||||||||
|x21-x20|<eps |
|-0,80-0|<0,1 |
|
|
|
|
|0,80|<0,1 нет |
|
|
|
|||||||||||||||
|x31-x30|<eps |
|0,41-0|<0,1 |
|
|
|
|
|0,41|<0,1 нет |
|
|
|
|||||||||||||||
Точность не достигнута, следовательно, продолжаем процесс вычисления.
Переходим к вычислению 2-ой итерации: |
|
||||||||||
i=1 |
|
|
|
|
|
|
|
|
|
|
|
12 = |
3 + 2 21 − 31 |
= |
3 + 2 (−0,80) − 0,41 |
|
|
= 0,12 |
|||||
8 |
|
|
|
|
|||||||
|
|
|
|
|
8 |
|
|
|
|
||
22 = |
−4 + 2 31 |
= |
−4 + 2 0,41 |
= −0,64 |
|||||||
|
|
5 |
|||||||||
|
5 |
|
|
|
|
|
|
|
|
||
32 = |
4 − 2 12 + 22 |
= |
4 − 2 0,12 + (−0,64) |
= 0,52 |
|||||||
6 |
|
|
6 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||
Проверим достигнута ли точность: |
|
|
|
|
|
||||||
|x12-x11|<eps |
|0,12-0,38|<0,1 |
|
|
|
|0,26|<0,1 нет |
|
|||||
|x22-x21|<eps |
|-0,64-(-0,80)|<0,1 |
|0,16|<0,1 нет |
|
||||||||
|x32-x31|<eps |
|0,52-0,41|<0,1 |
|
|
|
|0,11|<0,1 нет |
|
|||||
Точность не достигнута, следовательно, продолжаем процесс вычисления. Переходим к вычислению 3-ой итерации:
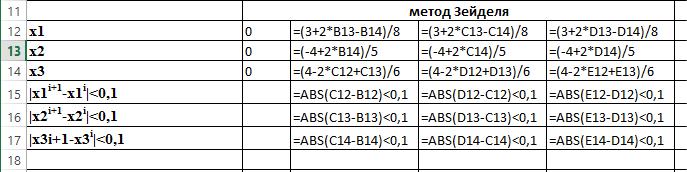
i=2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
= |
3 + 2 22 |
− 32 |
= |
3 + 2 (−0,64) − 0,52 |
= 0,15 |
||||||||
|
8 |
|
|
|
8 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
23 |
|
−4 + 2 32 |
−4 + 2 0,52 |
|
|
|
|||||||
|
= |
|
|
|
|
= |
|
|
= −0,59 |
|||||
|
|
5 |
|
|
5 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
33 |
= |
4 − 2 12 |
+ 22 |
= |
4 − 2 0,15 + (−0,59) |
= 0,52 |
||||||||
|
6 |
|
|
|
6 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Проверим достигнута ли точность: |
|
|
|
|
|
|||||||||
|x13-x12|<eps |
|0,15-0,12|<0,1 |
|
|
|
|0,03|<0,1 да |
|
||||||||
|x23-x22|<eps |
|-0,64-(-0,59)|<0,1 |
|0,05|<0,1 да |
|
|||||||||||
|x33-x32|<eps |
|0,52-0,52|<0,1 |
|
|
|
|0,00|<0,1 да |
|
||||||||
Вывод: точность достигнута, следовательно значения x1=0,15 x2=-0,59 x3=0,52 можно считать приближенным решением системы линейных уравнений с точностью 0,1.
Реализация в MS Excel
|
|
метод Зейделя |
|
||
x1 |
0 |
0,38 |
0,12 |
0,15 |
|
x2 |
0 |
-0,80 |
-0,64 |
-0,59 |
|
x3 |
0 |
0,41 |
0,52 |
0,52 |
|
|x1i+1-x1i|<0,1 |
|
ЛОЖЬ |
ЛОЖЬ |
ИСТИНА |
|
|x2i+1-x2i|<0,1 |
|
ЛОЖЬ |
ЛОЖЬ |
ИСТИНА |
|
|x3i+1-x3i|<0,1 |
|
ЛОЖЬ |
ЛОЖЬ |
ИСТИНА |
|
25

Реализация в Mcad
Лабораторная работа №3 Тема: Вычисление определенного интеграла
Тема: Вычисление определенного интеграла ∫ ( )
Постановка задачи: Дана интегрируемая функция f(x)=x2-3x, где х изменяется на интервале[-2;6,8] с шагом h.(n=8) Вычислить приближенное значение интеграла (выполнить ручной счет, реализацию в пакете MCAD, реализацию в табличном процессоре OpenOffice Calc (MS Excel) и рисунки методов) следующими
методами:1) левых прямоугольников; |
2) |
правых прямоугольников; |
3) центральных прямоугольников; 4) |
трапеций; 5) парабол (Симпсона) |
|
Ручной счет
Дана интегрируемая функция f(x)=x2-3x. Дан интервал [-2;6,8] и n=8.
а=-2 b=6,8.
Вычислим точное значение интеграла
|
3 |
2 |
|
6,8 |
3 |
2 |
|
(−2) |
3 |
|
3 (−2) |
2 |
|
|||||||
∫6,8(x2 − 3 x)dx = ( |
x |
− |
3 x |
) |
| |
= ( ( |
6.8 |
− |
3 6.8 |
) − ( |
|
− |
|
)) = |
||||||
|
|
|
|
|
|
|
|
|
||||||||||||
−2 |
3 |
2 |
|
−2 |
3 |
2 |
3 |
|
2 |
|
|
|||||||||
44,117 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обозначим точное значение IT=44,117 |
|
|
|
|
|
|
|
|
|
|||||||||||
Вычислим шаг h = |
(b−a) |
= |
(6,8−(−2)) |
= 1,1 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
n |
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Составим таблицу значений интегрируемой функции в точках разбиения интервала.
x |
|
|
|
|
f(x) |
|
|
x0=-2 |
|
x02 – 3* x0=(2)2 -3*(2)=10 |
|
|
|||
x1= x0+h=-2+1,1=-0,9 |
x12 – 3* x1=(-0,9)2 -3*(-0,9)= 3,51 |
|
|||||
x2= x1+h=-0,9+1,1=0,2 |
x22 – 3* x2=0,22 -3*0,2= -0,56 |
|
|
||||
x3= x2+h=0,2+1,1=1,3 |
x32 – 3* x3=1,32 -3*1,3= - 2,21 |
|
|||||
x4= x3+h=1,3+1,1=2,4 |
x42 – 3* x4=2,42 -3*2,4= - 1,44 |
|
|||||
x5= x4+h=2,4+1,1=3,5 |
x52 – 3* x5=3,52 -3*3,5= 1,75 |
|
|
||||
|
|
|
|
||||
x6= x5+h=3,5+1,1=4,6 |
x62 – 3* x6=4,62 -3*4,6=7,36 |
|
|
||||
x7= x6+h=4,6+1,1=5,7 |
x72 – 3* x7=5,72 -3*5,7= 15,39 |
|
|||||
x8= x7+h=5,7+1,1=6,8 |
x82 – 3* x8=6,82 -3*6,8= 25,84 |
|
|||||
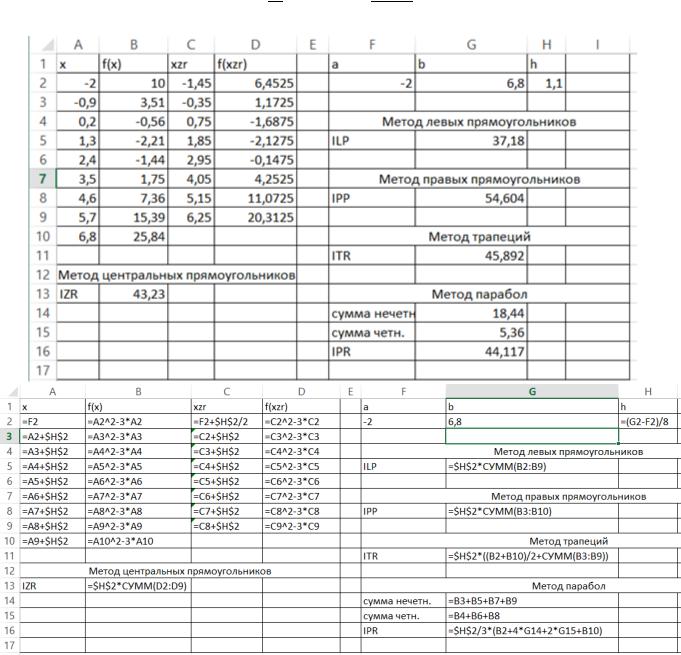
Метод левых прямоугольников |
|
|
|
|
|
||
Итерационная формула = ∑ −1 |
( ) |
|
|
|
|||
= ∑7 |
|
=0 |
|
|
|
|
|
( ) = ( ( ) + ( |
) + ( |
) + ( ) |
+ ( |
) + ( ) + |
|||
=0 |
|
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
||
( 6) + ( 7)) = 1,1 (10 + 3,51 + (−0,56) + (−2,21) + (−1,44) + 1,75 + 7,36 +
15,39) = 37,18
Вычислим погрешности вычислений Абсолютная погрешность ∆= | − | = |44,117 − 37,18| = 6,937
Относительная погрешность = |
∆ |
100% = |
6,937 |
|
100% ≈ 16% |
||
|
44,117 |
||||||
|
|
|
|
||||
Метод правых прямоугольников |
|
|
|
|
|
||
Итерационная формула = ∑ |
( ) |
|
|
|
|||
|
|
=1 |
|
|
|
|
|
27

= ∑8 |
( ) = ( ( ) + ( ) + ( |
) + ( ) + ( ) + ( ) |
+ |
|
||||||||||||||||||||
|
=1 |
|
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
5 |
6 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
( 7) + ( 8)) = 1,1 (3,51 + (−0,56) + (−2,21) + (−1,44) + 1,75 + 7,36 + |
|
|
||||||||||||||||||||||
15,39 + 25,84) = 54,604 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Вычислим погрешности вычислений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Абсолютная погрешность ∆= | − | = |44,117 − 54,604| = 10,487 |
|
|
||||||||||||||||||||||
Относительная погрешность = |
∆ |
|
100% = |
|
10,487 |
100% ≈ 24% |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
44,117 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Метод трапеций |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( )+ ( ) |
|
|
|
−1 |
|
|
|
|
|
||||||
Итерационная формула = ( |
0 |
|
|
+ ∑ |
|
|
|
( )) |
|
|
|
|
||||||||||||
|
2 |
|
|
|
=1 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= ( |
( 0)+ ( 8) |
+ ∑7 ( )) = ( |
( 0)+ ( 8) |
+ ( ) + ( |
) + ( ) |
+ |
||||||||||||||||||
|
|
|
||||||||||||||||||||||
2 |
|
=1 |
|
|
|
|
|
|
2 |
|
|
|
1 |
2 |
|
3 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
( 4) + ( 5) + ( 6) + ( 7)) = 1,1 ( |
10+25,84 |
+ 3,51 + (−0,56) + (−2,21) + |
|
|||||||||||||||||||||
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
(−1,44) + 1,75 + 7,36 + 15,39) = 45,892 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Вычислим погрешности вычислений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Абсолютная погрешность ∆= | − | = |44,117 − 45,892| = 1,775 |
|
|
||||||||||||||||||||||
Относительная погрешность = |
∆ |
|
100% = |
|
1.775 |
|
100% ≈ 4% |
|
|
|
||||||||||||||
|
44,117 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Метод парабол |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итерационная формула = |
|
( ( |
) + 4 C1 + 2 C2 + ( |
)) |
|
|
|
|||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
3 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Где C1 = ∑i f(xi) при i = 1,3,5,7. . n − 1 |
C2 = ∑i f(xi) при i = 2,4,6. . n − 2 |
|
|
|||||||||||||||||||||
= 3 ( ( 0) + 4 C1 + 2 C2 + ( 8))
1 = ( 1) + ( 3) + ( 5) + ( 7) = 3,51 + (−2,21) + 1,75 + 15,39 = 18,442 = ( 2) + ( 4) + ( 6) = (−0.56) + (−1.44) + 7.36 = 5.36
= 3 ( ( 0) + 4 C1 + 2 C2 + ( 8)) =
= 1,1 (10 + 4 18,44 + 2 5,36 + 25,84) = 44,117
Вычислим погрешности вычислений Абсолютная погрешность ∆= | − | = |44,117 − 44,117| = 0
Относительная погрешность = ∆ 100% = 44,1170 100% ≈ 0%
Метод центральных прямоугольников
Составим таблицу значений интегрируемой функции в центральных точках каждого интервала.
xzr |
|
|
|
f(xzr) |
xzr1=-1,45 |
xzr12 – 3* xzr1=(-1,45)2 -3*(-1,45)=6,452 |
|||
xzr 2= xzr 1+h=-1,45+1,1=- |
xzr 22 – 3* xzr |
2=(-0,35)2 -3*(-0,35)= 1,172 |
||
0,35 |
|
|
|
|
xzr 3= xzr 2+h=-0,35+1,1=0,75 |
xzr 32 – 3* xzr |
3=0,752 -3*0,75= -1,688 |
||
xzr 4= xzr 3+h=0,75+1,1=1,85 |
xzr 42 – 3* xzr |
4=1,852 -3*1,85= - 2,127 |
||
xzr 5= xzr 4+h=1,85+1,1=2,95 |
xzr 52 |
– 3* xzr |
5=2,952 |
-3*2,95= - 0,148 |
xzr 6= xzr 5+h=2,95+1,1=4,05 |
xzr 62 |
– 3* xzr |
6=4,052 |
-3*4,05= 4,253 |
|
|
|
|
|
xzr 7= xzr6+h=4,05+1,1=5,15 |
xzr 72 |
– 3* xzr |
7=5,152 |
-3*5,15=11,073 |
xzr 8= xzr7+h=5,15+1,1=6,25 |
xzr 82 |
– 3* xzr |
8=6,252 |
-3*6,25= 20,313 |
Итерационная формула = ∑ |
( ) |
=1 |
|
= ∑8=1 ( ) = ( ( 1) + ( 2) + ( 3) + ( 4) + ( 5) +( 6) + ( 7) + ( 8)) = 1,1 (6,452 + 1,172 + (1,688) + (−2,127) +
(−1,48) + 4,253 + 11,073 + 20,313) = 42,23
Вычислим погрешности вычислений Абсолютная погрешность ∆= | − | = |44,117 − 42,23| = 1,887
Относительная погрешность = ∆ 100% = 44,1171,887 100% ≈ 4%
Реализация в MS Excel
29
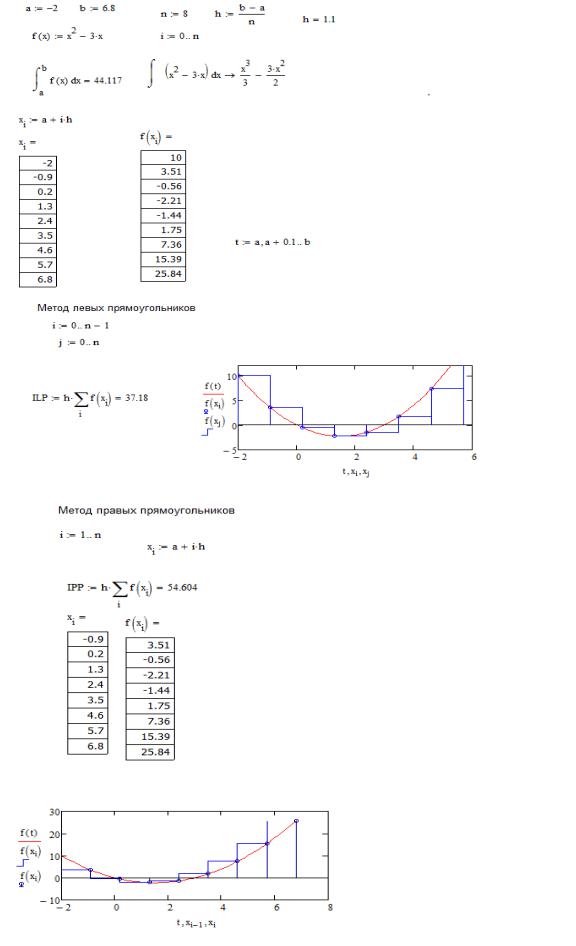
Реализация метода в Mcad
