
ТЕРВЕР alex_sasay
.pdf
ymin , ymax – соответственно минимальное и максимальное значение случайной величины Y;
ymini , ymaxi – соответственно минимальное и максимальное значение случайной величины Y на i-ом интервале монотонности.
49Закон распределения суммы случайных величин. Композиция законов распределения.
Одна из важнейших для практики частной задачи, а именно – нахождение закона распределения суммы двух случайных величин.
Пусть имеется система СВ (X,Y) с плотностью распределения f(x,y). Рассмотрим сумму СВ X и Y Z=X+Y и найдем закон распределения случайной величины Z. Для этого построим линию на плоскости ХОУ линию Z=X+Y. Она делит плоскость на две части Z>X+Y и Z<X+Y. Согласно определению функции распределения:
Дифференцируем это выражение по переменной Z, входящей в верхний предел внутреннего интеграла, получим
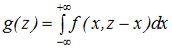 (13.1)
(13.1)
Это – общая формула для определения плотности распределения суммы двух случайных величин. Т.к. задача симметрична, то :
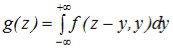 . (13.2)
. (13.2)
Особое практическое значение имеет случай, когда складываемые СВ (X,Y)
независимы. Тогда говорят о композиции законов распределения.
Для независимых случайных величин X и Y
f(x, y) = fх(x)fу(y) Þ (12.5) и (12.6) Þ Þ

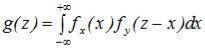 и
и 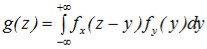 .
.
Для обозначения композиции законов применяют символическую запись:
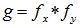 .
.
Закон распределения вероятностей называют устойчивым, если композиция таких законов есть тот же закон (отличающийся только параметрами). Нормальный закон обладает свойством устойчивости.
КОМПОЗИЦИЯ НОРМАЛЬНЫХ ЗАКОНОВ
Рассмотрим две независимые с.в. Х и У, подчиненные нормальным законам:
и
Требуется найти композицию этих законов, т.е. найти закон распределения величины Z=X+Y.
Применяем общую формулу для композиции законов распределения:
. (13.3)
Раскрываем скобки в показателе степени подынтегральной функции и приводим подобные члены, получаем
, (13.4)
где
Используя интеграл Эйлера-Пуассона: 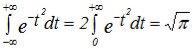 , получаем
, получаем
Подставляем значения А, В, С в эту формулу и после преобразований, получаем:

- это и есть нормальный закон с центром рассеивания 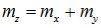 и средне квадратическим отклонением
и средне квадратическим отклонением
Итак, при композиции нормальных законов получается нормальный закон, причем МО и дисперсии(или квадраты с.к.о.) суммируются.
50Производящие функции.
В ряде случаев для определения важнейших числовых характеристик дискретных случайных величин может помочь аппарат производящих функций.
Пусть имеется дискретная случайная величина X, принимающая неотрицательные целочисленные значения 0, 1, …, k, … с вероятностями p0, p1, …, pk, …; pk=P{X=k}.
Производящей функцией случайной величины X называется функция вида:
где z – произвольный параметр(0<z≤1).
Очевидно, что
Возьмем первую производную по z от производящей функции:
и полагаем в ней z=1:
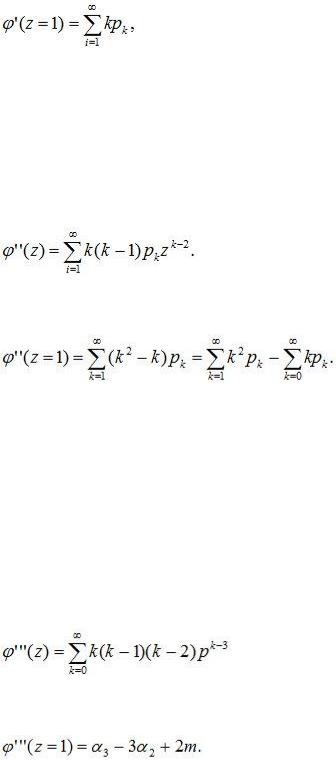
т.е. математическому ожиданию случайной величины X.
Таким образом, математическое ожидание неотрицательной целочисленной случайной величины равно первой производной ее производящей функции φ(z)
при z=1.
Возьмем вторую производную функции φ(z):
Полагая в ней z=1, получим
Первая сумма является вторым начальным моментом α2 случайной величины X, а вторая – ее математическое ожидание. Тогда:
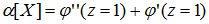 ,
,
т.е. второй начальный момент случайной величины равен сумме второй производной от производящей функции при z=1 плюс ее математическое ожидание.
Аналогично, берем третью производную:
и полагая в ней z=1, получаем:
И так далее, что позволяет выразить начальные моменты более высокого порядка.
51Характеристические функции.
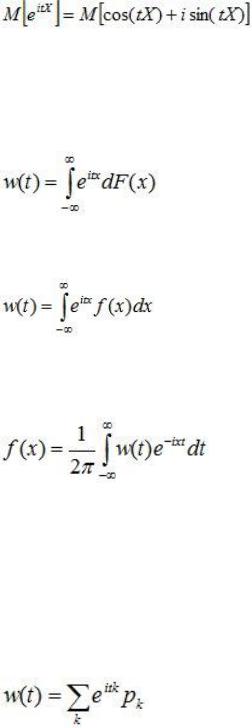
До сих пор мы задавали случайные величины законом распределения. Характеристическая функция - ещё один способ представления случайных величин.
Пусть X - случайная величина. Её характеристической функцией w(t) назовём математическое ожидание случайной величины eitX:
w(t)=MeitX,
где под комплексной случайной величиной eitX мы понимаем комплексное число eit X=cos(tX)+isin(tX), а
;
независимая переменная t имеет размерность X-1.
Характеристическая функция - преобразование Фурье-Стилтьеса функции распределения:
.
В непрерывном случае w(t) - преобразование Фурье плотности вероятности:
Если w(t) абсолютно интегрируема, то обратное преобразование Фурье позволяет восстановить плотность f(x) по характеристической функции:
.
В дискретном случае:
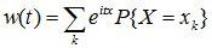 .
.
Особо отметим дискретные случайные величины с целочисленными значениями, например, при xk=k:

здесь w(t) - ряд Фурье в комплексной форме, вероятности pk играют роль коэффициентов Фурье и легко восстанавливаются по w(t):
.
В общем случае восстановление закона распределения по характеристической функции тоже возможно, но более сложно.
Свойства характеристических функций
Важнейшим свойством характеристической функции, сделавшим её одним из главных инструментов современной теории вероятностей, оказалось то, что при суммировании независимых случайных величин их характеристические функции перемножаются: если X и Y независимы, то для случайной
величины Z=X+Y: wZ(t)=wX(t)×wY(t).
Действительно,
wZ(t)=M(eitZ)=M(eit(X+Y))=M(eitX×eitY)=M(eitX)×M(eitY)=wX(t)×wY(t).
Законы распределения при суммировании независимых слагаемых ведут себя гораздо сложнее (см. Л12, закон распределения суммы случайных величин).
Если Y=aX+b, то
wY(t)=M(eit(aX+b))=eitb×M(eitaX)=eitb×wX(at).
Другим важным свойством характеристических функций является их простая связь с моментами.
Предполагая возможность дифференцирования под знаком математического ожидания в равенстве w(t)=MeitX, получим:
w(k)(t)=ikM(Xk×eitX).
При t=0:
Таким образом, характеристическая функция позволяет заменить интегрирование при вычислении моментов дифференцированием.
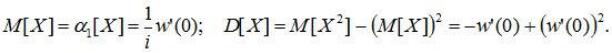
В частности,
Характеристическую функцию определяют также и для n-мерной случайной величины (X1, X2, , ¼ , Xn):
w(t1, t2, , ¼ , tn)=M(expi(t1X1+t2X2+¼+tnXn)).
