
ТЕРВЕР alex_sasay
.pdf
Доказательство: следует из свойств 1 и 3.
4.Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:
M[X+Y] = M[X]+M[Y]. (6.6)
23Дисперсия случайной величины и ее свойства.
Дисперсия случайной величины есть математическое ожидание квадрата соответствующей центрированной случайной величины.
Она характеризует степень разброса значений случайной величины относительно ее математического ожидания, т.е. ширину диапазона значений.
Расчетные формулы:
(6.9)
Дисперсия может быть вычислена через второй начальный момент:
(6.10)
Дисперсия случайной величины характеризует степень рассеивания (разброса) значений случайной величины относительно ее математического ожидания. Дисперсия СВ (как дискретной, так и непрерывной) есть неслучайная (постоянная) величина.
Дисперсия СВ имеет размерность квадрата случайной величины. Для наглядности характеристики рассеивания пользуются величиной, размерность которой совпадает с размерностью СВ.
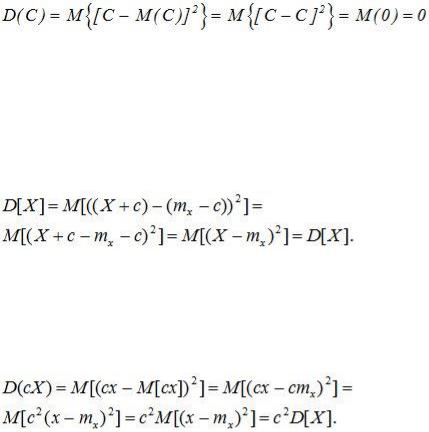
Средним квадратическим отклонением (СКО) СВ X называется характеристика
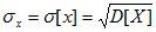 . (6.11)
. (6.11)
СКО измеряется в тех же физических единицах, что и СВ, и характеризует ширину диапазона значений СВ.
Свойства дисперсии
Дисперсия постоянной величины с равна нулю.
Доказательство: по определению дисперсии
При прибавлении к случайной величине Х неслучайной величины с ее дисперсия не меняется.
D[X+c] = D[X].
Доказательство: по определению дисперсии
(6.12)
3. При умножении случайной величины Х на неслучайную величину с ее дисперсия умножается на с2.
Доказательство: по определению дисперсии
. (6.13)
Для среднего квадратичного отклонения это свойство имеет вид:
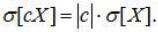 (6.14)
(6.14)
Действительно, при ½С½>1 величина сХ имеет возможные значения (по абсолютной величине), большие, чем величина Х. Следовательно, эти значения рассеяны вокруг математического ожидания М[сХ] больше, чем возможные
значения Х вокруг М[X], т.е. 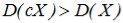 . Если 0<½с½<1, то
. Если 0<½с½<1, то 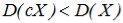 .
.
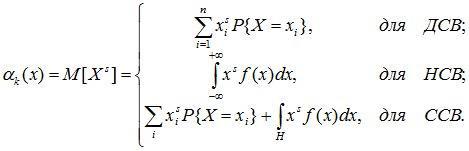
Правило 3s. Для большинства значений случайной величины абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения, или, другими словами, практически все значения СВ находятся в интервале:
[ m - 3s; m + 3s; ].(6.15)
24Моменты высших порядков.
Понятие момента широко применяется в механике для описания распределения масс (статические моменты, моменты инерции и т.д.). Теми же приемами пользуются и в теории вероятностей. Чаще на практике применяются моменты двух видов: начальные и центральные.
Начальный момент s-го порядка СВ X есть математическое ожидание s-й степени этой случайной величины: as = M[Xs].
(6.7)
Математическое ожидание случайной величины является начальным моментом первого порядка
Центрированной случайной величиной называется отклонение случайной величины от ее математического ожидания:
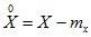 .
.
Центрирование случайной величины аналогично переносу начала координат в среднюю, «центральную» точку, абсцисса которой равна математическому ожиданию случайной величины.
Центральным моментом s-го порядка СВ X есть математическое ожидание s-й степени центрированной случайной величины: ms = M[(X-mx) s].
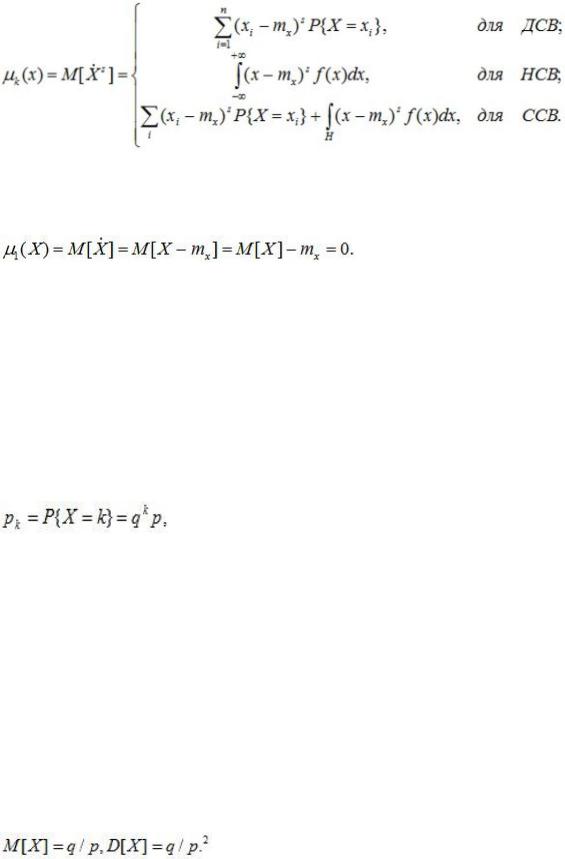
(6.8)
Очевидно, что для любой случайной величины Х центральный момент первого порядка равен нулю:
Аналогично можно получить моменты не только относительно начала координат (начальные моменты) или математического ожидания (центральные моменты), но и относительно произвольной точки а.
25Геометрическое распределение.
Дискретная случайная величина X имеет геометрическое распределение, если вероятности ее возможных значений 0,1,….,k,.. определяются так:
где p – параметр распределения, 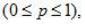 а q=1-p.
а q=1-p.
 0 1 2 … k …
0 1 2 … k … 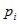 p
p 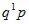
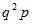 …
… 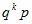 …
…
На практике геометрическое распределение появляется при следующих условиях. Пусть производится некоторый опыт, в котором некоторое событие появляется с вероятностью p. Опыты производятся последовательно, до наступления события. Случайная величина X, равная числу неудачных опытов, имеет геометрическое распределение.
Числовые характеристики геометрического распределения:
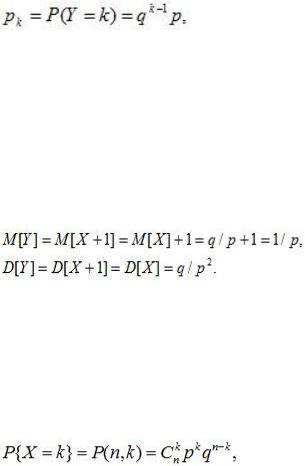
26Смещенное геометрическое распределение.
“Смещенное” геометрическое распределение получается из геометрического путем преобразования СВ X и СВ Y=X+1.
Дискретная случайная величина Y имеет смещенное геометрическое распределение если вероятности ее возможных значений 1,…,k, определяются так
где p – параметр распределения 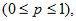 а q=1-p.
а q=1-p.
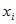 1 2 3 … k …
1 2 3 … k … 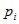 p
p 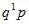
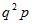 …
… 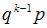 …
…
Числовые характеристики смещенного геометрического распределения определяются с использованием их свойств:
27Биномиальное распределение.
Дискретная случайная величина X имеет биноминальное распределение, если ее
закон распределения описывается формулой Бернулли:
где p – параметр распределения 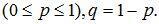
Распределение загасит от двух параметров п и р.
На практике биноминальное распределение возникает при следующих условиях. Пусть производится серия из п испытании, в каждом из которых некоторое событие появляется с вероятностью р. Случайная величина X, равная числу наступлений события в п опытах, имеет биноминальное распределение.
Числовые характеристики: М [Х] = n, D[X]= npq.
Название объясняется тем, что правую часть равенства можно рассматривать как общий член разложения Бинома Ньютона:
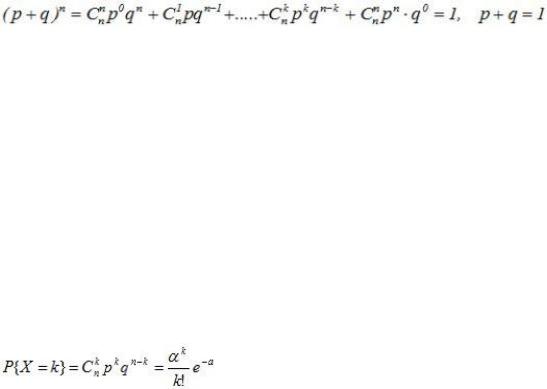
,
т.е. 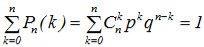 .
.
28Распределение Пуассона.
Соотношениями, описывающими биноминальное распределение, удобно пользоваться в тех случаях, если величина и достаточно мала, а р велико.
Теорема: Если, 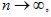 а
а 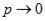 так, что
так, что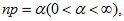 то
то
при любом k=0,1,….
Числовые характеристики: М[Х] = α, D[X] = α.
Закон Пуассона зависит от одного параметра α, смысл которого заключается в следующем: он является одновременно и математическим ожиданием и дисперсией случайной величины Х.
29Простейший поток событий.
Физические условия возникновения распределения.
Рассмотрим временную ось, на которой будем отмечать моменты возникновения случайных событий (например, отказы компонентов в сложном техническом устройстве, заявки на обслуживание).
Поток случайных событий называется стационарным, если число событий, приходящихся на интервал t в общем случае не зависит от расположения этого участка на временной оси и определяется только его длительностью, т.е. среднее число событий в единице времени (l) (интенсивность потока) постоянно.
Поток случайных событий называется ординарным, если вероятность попадания в некоторый участок Dt двух и более случайных событий пренебрежимо мала по сравнению с вероятностью попадания на него одного события.
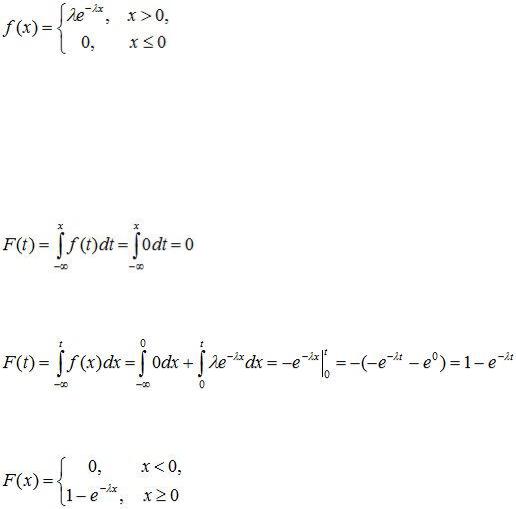
В потоке отсутствует последействие, если вероятность попадания событий на участок t не зависит от того, сколько событий попало на другие участки, не пересекающиеся с данным.
Поток случайных событий называется простейшим, или Пуассоновским, если он является стационарным, ординарным и без последействия.
Для Пуассоновского потока число событий поступивших в течение интервала t является дискретной случайной величиной с распределением Пуассона с параметром α = tl
30Экспоненциальное распределение случайной величины.
Непрерывная случайная величина Х, принимающая только положительные значения имеет показательное (или экспоненциальное) распределение, если
, (8.8)
Положительная величина l называется параметром показательного распределения и полностью определяет его.
Определим функцию распределения случайной величины.
1. при t<0
,
2. при t≥0
.
Таким образом, функция распределения имеет вид:
(8.9)
Числовые характеристики случайной величины.
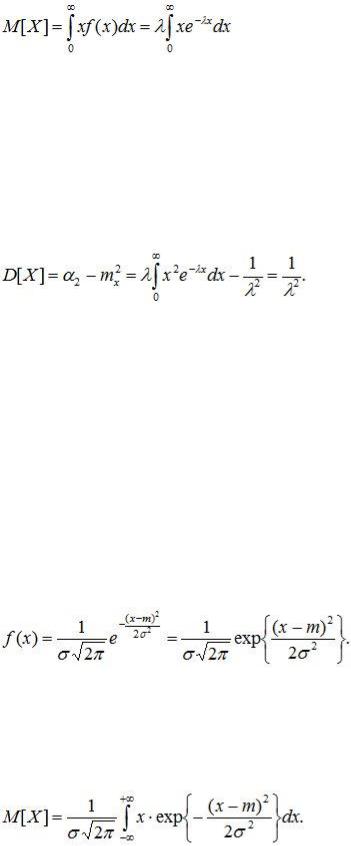
.
Проводя интегрирование по частям и учитывая, что при x→∞ e-x стремиться к нулю быстрее, чем возрастает любая степень x , находим:
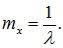 (8.10)
(8.10)
Дисперсия случайной величины определяем по формуле:
(8.11)
Показательное распределение тесно связано с простейшим (стационарным пуассоновским) потоком событий. Интервал времени T между двумя соседними событиями в простейшем потоке имеет показательное распределение с параметром, равным интенсивности потока.
31Нормальное распределение
Непрерывная случайная величина Х имеет нормальное распределение, если ее
плотность вероятности имеет вид:
(8.12)
Определим числовые характеристики нормально распределенной случайной величины Х. Математическое ожидание:
Применяя замену переменной
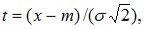 (8.13)
(8.13)
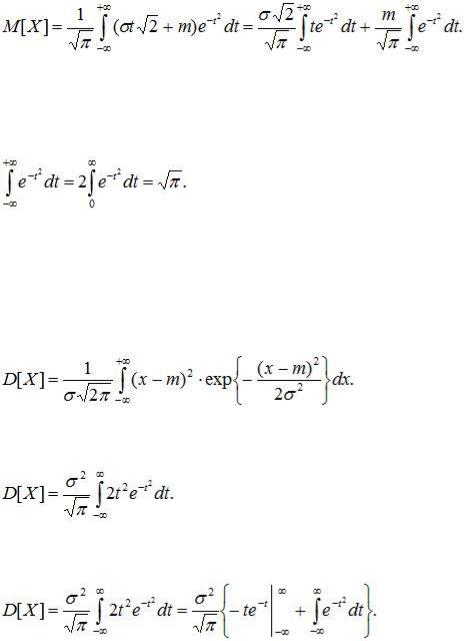
получим
В полученном выражении первый интеграл равен нулю (интеграл в симметричных пределах от нечетной функции), а второй интеграл есть интеграл Эйлера-Пуассона:
(8.14)
Таким образом, математическое ожидание величины Х равно m:
M[X]=m.
Вычислим дисперсию СВ Х:
Применяя замену переменной (8.13) получим:
Интегрируя по частям, получим:
Первое слагаемое в фигурных скобках равно нулю (т.к. 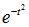 при t→∞ убывает быстрее, чем возрастает любая степень t), второе слагаемое, согласно (8.14),
при t→∞ убывает быстрее, чем возрастает любая степень t), второе слагаемое, согласно (8.14),
равно 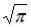 , откуда
, откуда
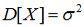 .
.
Таким образом, нормальное распределение случайной величины полностью описывается двумя числовыми характеристиками: математическим ожиданием M[X] и средним квадратичным отклонением σ.
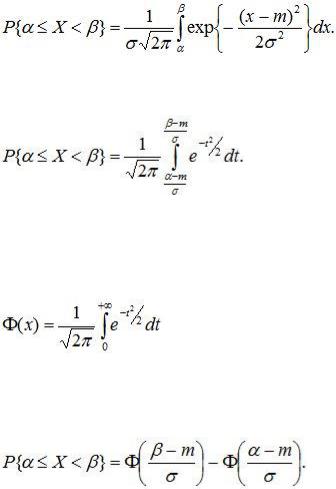
Рассмотрим влияние параметров m и σ на кривую распределения. При изменении параметра m кривая f(x), не изменяя формы, будет смещаться вдоль оси абсцисс. Изменение σ равносильно изменению масштаба кривой по обеим осям; например, при удвоении σ масштаб по оси абсцисс удвоится, а по оси ординат уменьшится в два раза (рис. 8.3).
Центральные моменты нечетной степени для нормально распределенной случайной величины определяются равны нуню; для вычисления центральных моментов четной степени используется рекуррентное соотношение следующего вида:
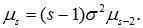 (8.15)
(8.15)
Определим вероятность попадания нормально распределенной случайной величины в интервал от α до β:
Сделав замену переменной t=(x-m)/σ, получим:
Так как первообразная для e-x не выражается через элементарные функции, то для вычисления вероятностей событий, связанных с нормальными случайными величинами используют табулированную функцию Лапласа:
.
С помощью этой функции вероятность попадания нормально распределенной случайной величины на интервал от α до β определится так:
(8.16)
Функция Лапласа обладает следующими свойствами:
1.Φ(0)=0;
2.Φ(-х)=-Φ(х);
3.Φ(-∞)=0,5.
