
Skhemotekhnika_1
.pdf
Для узлов цепей переменного тока в каждый момент времени справедлив первый закон Кирхгофа. Из этого следует, что он справедлив также и для комплексных амплитуд токов, втекающих в узел из различных
|
проводников. |
|
Итак, для цепей переменного тока |
|
справедливы как закон Ома, так и правило |
|
узлов. Из этого следует, что при анализе |
Рис. 6.4. Линейные элементы |
цепей переменного тока можно применять |
те же самые методы, что и для расчета |
|
цепей переменного тока |
цепей постоянного тока, только токи сле- |
дует интерпретировать как комплексные амплитуды переменных токов, а потенциалы — как комплексные амплитуды переменных потенциалов.
Широкое распространение на практике для расчета цепей переменного синусоидального тока получил метод комплексных амплитуд. Его еще называют символическим или комплексным.
Сущность метода комплексных амплитуд состоит в том, что при синусоидальном токе можно перейти от уравнений, составленных для мгновенных значений и являющихся дифференциальными уравнениями, к алгебраическим уравнениям, составленным относительно комплексных амплитуд тока и напряжения. Этот переход основан на том, что в любом уравнении, составленном по законам Кирхгофа для
установившегося процесса, |
мгновенное значение тока |
i заменяют |
комплексной амплитудой тока I&0 ; мгновенное значение напряжения |
||
на активном сопротивлении |
uR = Ri заменяют на RI&0 ; мгновенное |
|
значение напряжения на индуктивности uL = L di dt |
заменяют на |
|
I&0 jωL ; мгновенное значение напряжения на емкости |
uC = (òidt) C |
|
|
заменяют на I&0 (− j (ωC)); ЭДС e за- |
|
|
& |
|
|
заменяют на E0 . |
|
|
Например, для схемы, изображен- |
|
|
ной на рис. 6.5, уравнение для мгно- |
|
|
венных значений можно записать так: |
|
Рис. 6.5. Расчет схемы с помощью |
uR + uL + uC = e , |
|
метода комплексных амплитуд |
или |
|
|
|
61 |

|
|
iR + L |
di |
|
+ |
1 |
òidt = e . |
||||||||||
|
|
dt |
C |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Запишем его в комплексной форме: |
|
|
|
||||||||||||||
& |
& |
|
|
|
|
& |
æ - j |
ö |
|
& |
|||||||
I |
|
R + I |
|
jwL |
+ I |
|
ç |
|
|
|
÷ = |
E . |
|||||
|
|
|
|
|
|
||||||||||||
|
0 |
|
0 |
|
|
|
|
|
|
0 |
è wC |
ø |
|
0 |
|||
Из последнего выражения следует, что для схемы, показанной |
|||||||||||||||||
на рис. 6.5, справедливо выражение: |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
I&0 = |
|
|
|
|
|
E0 |
|
|
|
. |
|
||||
|
|
|
R + jwL - |
j |
|
||||||||||||
|
|
|
|
|
wC |
|
|||||||||||
Пример 6.1. На вход цепи, изобра- |
|
||||||||||||||||
|
|
|
|
|
|||||||||||||
женной на рис. 6.6, подается перемен- |
|
|
|
|
|
||||||||||||
ное напряжение с амплитудой U1 |
и час- |
|
|
|
|
|
|||||||||||
тотой f. Найти амплитуду выходного |
|
|
|
|
|
||||||||||||
напряжения и его фазовый сдвиг отно- |
|
|
|
|
|
||||||||||||
сительно входного. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Обозначим комплексную |
|
|
Рис. 6.6. Резистивно-емкостной |
||||||||||||||
амплитуду входного переменного на- |
|
|
|||||||||||||||
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
делитель напряжения |
пряжения через U1 , а комплексную ам- |
|
|
|
|
|
||||||||||||
плитуду выходного — через U&2 . Поскольку рассматриваемая цепь
представляет собой делитель напряжения, комплексные амплитуды
входного |
и |
выходного |
|
напряжений |
|
|
связаны |
|
|
соотношением: |
||||||||||||||||||||||||||||||
& |
& |
|
|
(ZR + ZC ), где ZR — импеданс резистора, ZR = R , а ZC — |
||||||||||||||||||||||||||||||||||||
U2 |
= U1ZR |
|||||||||||||||||||||||||||||||||||||||
импеданс конденсатора, ZC = 1 jwC . Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
& |
& |
|
|
|
|
R |
|
|
|
|
|
& |
|
|
jwRC |
|
. |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
U |
2 =U1 |
|
|
|
|
|
=U1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
R +1 (jwC) |
1 + jwRC |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
Для того чтобы найти амплитуду выходного напряжения необ- |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
: |
|
|
|
|
|
|
|
|
|
|
|
ходимо вычислить модуль комплексного числа U2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
jwRC |
|
|
|
|
|
|
|
jwRC |
|
|
|
|
|
|
|
æ |
jwRC |
|
öæ |
|
|
jwRC |
ö |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
& |
|
& |
|
|
|
|
& |
|
|
|
|
|
|
& |
|
|
ç |
|
֍ |
|
|
÷ |
|
||||||||||||||||
|
U2 |
= |
U1 |
|
|
|
|
|
|
= |
U1 |
´ |
|
|
|
|
= |
|
U1 |
´ |
ç |
|
|
|
|
|
֍ |
|
|
|
|
÷ |
= |
|||||||
|
|
|
|
1 |
+ jwRC |
|
|
|
|
1 |
+ |
jwRC |
|
|
|
|
|
|
è |
1 + jwRC |
øè1 + jwRC ø |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
æ |
|
|
|
|
|
|
|
öæ |
|
|
|
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
jwRC |
- jwRC |
|
|
|
|
|
|
|
2 |
|
2 |
C |
2 |
|
|
|
|
||||||||||||||
|
|
|
|
= |
& |
´ |
ç |
|
֍ |
|
÷ |
|
= |
& |
|
´ |
|
w |
R |
|
|
|
|
|
||||||||||||||||
|
|
|
|
U1 |
ç |
1 + jwRC |
֍ |
|
|
|
÷ |
|
U1 |
|
|
|
2 |
|
2 |
C |
2 = |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
è |
øè |
1 - jwRC ø |
|
|
|
|
|
1 + w |
R |
|
|
|
|
|||||||||||||||||||
62 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

= |
|
& |
|
× |
|
|
ωRC |
|
|
& |
|
× |
|
2πf RC |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
U1 |
|
|
|
|
|
= |
|
U1 |
|
|
|
|
. |
|||
|
|
|
+ ω2 R2C 2 |
1 + (2πf )2 R2C 2 |
|||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||
Чтобы найти фазовый сдвиг выходного напряжения, необходимо вычислить действительную и мнимую составляющие комплексной амплитуды выходного напряжения Re(U&2 ) и Im(U&2 ), и воспользоваться формулой ϕ = arctg(Im(U&2 )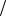 Re(U&2 )):
Re(U&2 )):
& |
& |
|
jwRC |
|
& |
|
|
jwRC(1 - jwRC) |
|
|
|
|
|
|
|
|
|
|
||||||||
U 2 |
= U |
1 |
|
|
= U1 |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
||||||
1 + jwRC |
(1 + jwRC)(1 - jwRC) |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
& jwRC + w2 R2C 2 |
& |
|
w2 R2C 2 |
|
|
|
& |
|
|
|
wRC |
|
|||||||||||
|
|
= U1 |
|
|
= U |
1 |
|
|
|
+ jU1 |
|
; |
||||||||||||||
|
|
1 + w2 R2C 2 |
1 + w2 R2C 2 |
1 + w2 R2C 2 |
||||||||||||||||||||||
|
|
æ |
|
& |
|
) |
ö |
æ |
|
|
wRC |
2 |
2 |
C |
2 |
ö |
|
|
||||||||
|
|
|
|
|
Im(U |
2 |
|
|
|
|
|
|
w |
R |
|
|
|
|||||||||
|
j = arctgç |
|
|
|
|
÷ = arctgç |
|
|
|
|
|
|
|
|
|
÷ |
= |
|
||||||||
|
|
& |
|
|
|
|
2 2 2 |
|
|
|
|
|
2 |
2 2 |
|
|||||||||||
|
|
ç |
|
|
|
÷ |
ç |
|
+ w R C 1+ w R C |
÷ |
|
|
||||||||||||||
|
|
|
|
è Re(U2 ) |
ø |
è1 |
ø |
|
|
|||||||||||||||||
æ |
1 ö |
æ |
1 |
ö |
||
ç |
÷ |
|||||
= arctgç |
|
÷ |
|
|||
= arctgç |
|
÷. |
||||
è wRC ø |
è |
2pf RC ø |
||||
При рассмотрении цепей переменного тока большую роль играет частотная характеристика цепи. Если на входе цепи переменный сигнал имеет комплексную амплитуду U&1 , а на выходе — U&2 , (такую цепь принято называть четырехполюсником), то частотной характеристикой (или передаточной функцией) называется отношение этих комплексных амплитуд, которое в общем случае зависит от частоты: H& (ω)= U&2  U&1 . Поскольку частотная характеристика являет-
U&1 . Поскольку частотная характеристика являет-
ся комплексной величиной, можно выделить ее амплитуду и фазу:
H& (ω)= H (ω)e jϕ(ω) = Re H& (ω)+ j Im H& (ω);
|
|
|
|
|
|
|
|
|
& |
|
|
& |
|
& |
|
& |
|
|
|
|
|
|
|
2 |
2 |
|
|
Im H (ω) |
|
|||
H (ω)= |
H (ω) |
= |
[Re H (ω)] |
|
+ [Im H (ω)] |
|
; |
ϕ(ω)= arctg |
& |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Re H (ω) |
|
Амплитуда частотной характеристики называется амплитудно-
частотной характеристикой (АЧХ), а ее фаза — фазово-частотной характеристикой (ФЧХ). В рассмотренном примере частотная характеристика цепи равна jωRC (1+ jωRC), а ее АЧХ и ФЧХ — соответсвенно ωRC
(1+ jωRC), а ее АЧХ и ФЧХ — соответсвенно ωRC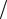

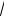 1+ ω2R2C2 и arctg(1
1+ ω2R2C2 и arctg(1 ωRC).
ωRC).
63
Пример 6.2. Найти амплитудно-частотную и фазово-частотную характеристики моста Вина-Робинсона (рис. 6.7).
Решение. На вход схемы, показанной на рис. 6.7 сигнал подается относительно общей точки (т.е. точки, которая имеет нулевой потенциал). Выходной сигнал снимается между точками a и b. На входе
схемы переменный сигнал имеет комплексную амплитуду U&1 , а на выходе — U&2 . В точке a относительно общей точки омический делитель напряжения обеспечивает частотно-независимое напряжение
& & |
|
R1 |
|
1 |
& |
Ua = U1 |
R + 2R |
= |
3 |
U1 . |
|
1 |
1 |
|
|
|
|
В точке b относительно общей точки напряжение будет иметь значение:
& |
& |
|
|
|
1 [(1 R)+ jwC] |
|
|
|
Ub = U1 |
|
|
|
|
= |
|||
[1 |
(1 R)+ jwC]+ R + (1 jwC) |
|||||||
|
|
& |
|
jwRC |
|
|
||
|
= U1 |
|
|
= |
|
|||
|
(jwRC +1)2 + jwRC |
|
||||||
|
|
& |
|
jwRC |
|
|
||
|
= U1 |
|
|
= |
|
|||
|
(jwRC +1)2 + jwRC |
|
||||||
|
|
|
|
& |
jW |
|
|
|
Рис. 6.7. Мост Вина-Робинсона |
|
|
=U1 |
|
, |
|
|
|
|
|
(1 + 3 jW - W2 ) |
|
|
||||
где введено обозначение W = wRC . Выходной сигнал равен разности потенциалов точек a и b:
|
|
& |
|
& |
& |
|
|
1 & |
|
|
|
|
jW |
& |
|
|
|
||||||||||
|
|
U2 |
= Ua -Ub = |
|
U1 |
- |
|
|
|
|
U1 . |
|
|||||||||||||||
|
|
3 |
1+ 3 jW - W2 |
|
|||||||||||||||||||||||
|
Отсюда следует, что |
|
|
|
|
|
|
(1- W2 )(3 - 3W2 )- j9W(1- W2 ) |
|
||||||||||||||||||
& |
& |
& |
1 |
|
|
1- W2 |
|
|
|
|
|
|
|
||||||||||||||
H (w)= U2 |
U1 = |
|
× |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
. |
|||
3 |
|
|
|
|
|
|
|
|
|
|
(3 - 3W2 )2 |
+ (9W)2 |
|||||||||||||||
|
|
|
1 |
+ 3 jW - W2 |
|
|
|
|
|
||||||||||||||||||
|
АЧХ и ФЧХ определяются как |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
1- W2 |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Н (w) = |
|
Н (w) |
|
= |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
(1- W2 )2 + 9W2 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
64
j(w) = arctg |
3W |
, W ¹1. |
|
||
|
W2 -1 |
|
Строить графики АЧХ четырехполюсников принято в двойном логарифмическом масштабе, удобном для отображения как очень низких, так и очень высоких частот. При использовании логарифмического масштаба относительные изменения величины отображаются на графике одинаковыми интервалами. Положения меток частот на горизонтальной оси определяются формулой l = l0 lg(f  f0 ), где частота f0 выбирается из удобства построения графика (вертикальная ось графика будет пересекать горизонтальную именно в частоте f0), а величина l0 определяет масштаб по горизонтальной оси (длина l0 в мм, см и т.д. соответствует десятикратному увеличению частоты), а по вертикальной оси откладывается АЧХ, выраженная в децибеллах, то есть величина 20lg H& (w) .
f0 ), где частота f0 выбирается из удобства построения графика (вертикальная ось графика будет пересекать горизонтальную именно в частоте f0), а величина l0 определяет масштаб по горизонтальной оси (длина l0 в мм, см и т.д. соответствует десятикратному увеличению частоты), а по вертикальной оси откладывается АЧХ, выраженная в децибеллах, то есть величина 20lg H& (w) .
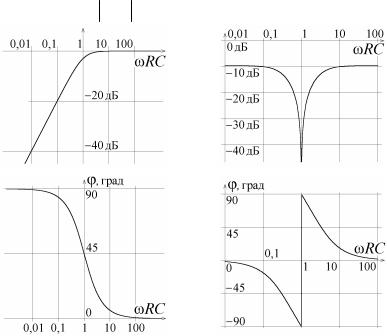
Рис. 6.8. АЧХ (вверху) и ФЧХ (внизу) |
Рис. 6.9. АЧХ (вверху) и ФЧХ (внизу) |
резистивно-емкостного делителя |
моста Вина-Робинсона |
65

Пример 6.3. АЧХ некоторой цепи имеет на некоторой частоте значение 1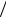

 2 ≈ 0,707 . Найти ее значение в децибеллах.
2 ≈ 0,707 . Найти ее значение в децибеллах.
Решение.
HдБ = 20lg(1 
 2 )= −20lg
2 )= −20lg 
 2 = −20 × 1 lg2 = −10 × 0,301 = −3,01дБ . 2
2 = −20 × 1 lg2 = −10 × 0,301 = −3,01дБ . 2
На рис. 6.8 и 6.9 приведены амплитудно-частотные и фазовочастотные характеристики резистивно-емкостного делителя и моста Вина-Робинсона. Для изображения графика АЧХ использован двойной логарифмический масштаб, на графике ФЧХ логарифмический масштаб используется только для оси частот, значения фазы приведены в линейном масштабе.
Контрольные вопросы
1. Два переменных сигнала связаны соотношением U1(t)= −U2 (t). Найти фазовый сдвиг между этими сигналами.
2.Изобразить два переменных сигнала одинаковых амплитуд, сдвинутых по фазе один относительно другого на 120°.
3.Может ли импеданс конденсатора на какой-либо частоте равняться импедансу катушки индуктивности?
4.Может ли АЧХ принимать отрицательные значения?
5.Вычислить АЧХ и ФЧХ резистивного делителя напряжения.
6.Пусть АЧХ на частоте ω = 0 имеет значение 1. Отобразить этот факт в двойном логарифмическом масштабе.
7.Пусть АЧХ на частоте ω0 имеет значение 0. Отобразить этот факт в двойном логарифмическом масштабе.
Программа лабораторной работы
1. Получить у преподавателя схему цепи переменного тока.
66
2.Методом комплексных амплитуд рассчитать частотную характеристику цепи, ее АЧХ и ФЧХ.
3.Собрать полученную схему.
4.Подключить к входу цепи генератор переменного напряжения. Изменяя частоту генератора, измерить с помощью осциллографа отношение амплитуды выходного сигнала к амплитуде входного и фазовый сдвиг между сигналами для разных частот.
5.Пользуясь полученными результатами, построить АЧХ и ФЧХ исследуемой цепи. При построении ФЧХ для оси частот использовать логарифмический масштаб, а для оси значений — линейный. При построении АЧХ использовать двойной логарифмический масштаб. На тех же графиках построить рассчитанные АЧХ и ФЧХ.
6.На построенном графике АЧХ исследуемой цепи отметить частоты, на которых АЧХ имеет значение 1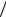

 2 .
2 .
Содержание отчета
Отчет должен содержать:
1.Полученную схему цепи переменного тока и расчет ее частотной характеристики методом комплексных амплитуд.
2.Таблицу результатов измерений АЧХ и ФЧХ.
3.Построенные на одном графике в двойном логарифмическом масштабе рассчитанную и измеренную АЧХ.
4.Построенные на одном графике в логарифмическом масштабе рассчитанную и измеренную ФЧХ.
5. Значения частот, на которых АЧХ цепи принимает значение 1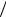

 2 .
2 .
67

Задачи для самостоятельного решения
Согласно программе лабораторной работы провести исследования следующих схем:
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
68

9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
69

ТЕМА 7. КОЛЕБАТЕЛЬНЫЙ КОНТУР
последовательный колебательный контур резонансная частота контура характеристическое сопротивление контура резонанс напряжений параллельный колебательный контур резонанс токов ширина полосы пропускания добротность
свободные колебания контура
Колебательные контуры, т.е. цепи, содержащие конденсаторы и катушки индуктивности (реактивные элементы), широко применяются в радиотехнических устройствах. При этом используются резонансные свойства колебательных контуров. Частотная характеристика такой цепи обязательно содержит член вида (ω2LC −1) , который обращается в ноль при частоте входного сигнала ωp =1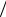

 LC . Это зна-
LC . Это зна-
чение частоты обычно называется резонансной частотой контура.
В зависимости от способа соединения конденсатора и катушки индуктивности различают последовательный колебательный контур (конденсатор и катушка индуктивности соединены последовательно) и параллельный колебательный контур (конденсатор и катушка индуктивности соединены параллельно).
Рассмотрим некоторые типичные схемы. На рис. 7.1 изображен последовательный колебательный контур. Определим ток в контуре при подключении к нему источника переменного напряжения. Применяя метод комплексных амплитуд, представим комплексную амплитуду тока в виде следующего выражения:
|
& |
|
& |
|
|
& |
|
& |
|
|
|
|||||
|
|
|
|
|
U |
|
||||||||||
I& = |
U |
= |
U |
= |
|
|
U |
= |
|
|
|
|
|
e− jϕ , |
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Z |
R + jωL − j (ωC) |
|
|
Z |
|
e jϕ |
|
|
Z |
|
|
|||||
|
|
|
|
|||||||||||||
где
Z= R + j(ωL −1 ωC) —
ωC) —
—комплексное сопротивление последовательного контура,
70
