ЛР_3

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное образовательное

учреждение высшего образования

«Юго-Западный государственный университет»

Лабораторная работа №3

По дисциплине «Математическая логика и теория алгоритмов»

Вариант №5

Выполнил: Бунина А.В.

студент группы ИБ-01б

Проверил: Добрица В.П.

профессор

Курск, 2021

Задача 1. Найдите сокращенную, все тупиковые и минимальные ДНФ булевой функции методом Квайна:

1. f (0,0,0) = f (0,0,1) = f (1,0,1) = f (1,1,1) = 0

2. f (0,0,0) = f (0,0,1) = f (1,0,0) = f (1,1,0) = f (1,1,1) = 1

Решение:

а) если ДНФ булевой функции f не содержит отрицаний переменных, то эта форма будет являться единственной МДНФ, а значит, она будет наименьшей.

Рассмотрим булеву функцию f, заданную равенствами:

f (0,0,0) = f (0,0,1) = f (1,0,1) = f (1,1,1) = 0

Для этой функции СДНФ является выражение:

(Пояснить как получили. Это для ДНФ? Повторите алгоритм построения ДНФ.)

Проводя сокращения по законам логики, получим тупиковую ДНФ:

Эту формулу можно получить, исходя из наборов значений переменных, что равносильно преобразованиям по законам логики.

Так, наборы (0,0,0) и (0,0,1) различаются по значениям только одной переменной . Это означает, что независимо от значения первой переменной при фиксированных значениях других переменных, значение функции будет равно 0. Тогда эти наборы можно объединить, ставя прочерк вместо последней переменной: (0,0, _).

Проводя подобные объединения по всем наборам, мы получим следующие наборы с прочерками, которые больше не сокращаются: (1,1,_) (0,_,0) (_,1,0)

Тупиковую нормальную форму можно получить не преобразованиями по законам логики, а проводя рассуждения с наборами значений переменных, на которых функция принимает значение 0, и восстанавливая ее по полученным сокращенным наборам значений переменных.

Составим таблицу (Квайна), показывающую соответствие элементарных импликант и наборов значений переменных функции по значениям 0 данной функции:

Элементарные импликанты	Сокращенные наборы	Наборы значений переменных, определяющие 0 булевой функции
		000	001	101	111
	00_	0	0
	_01		0	0
	1_1			0	0

Отметим, что есть столбцы, в которых только одна 0. Это значит, что для данного полного набора значений переменных только одна элементарная импликанта дает значение 0 («перекрывает» данный набор). Следовательно, такая импликанта обязательно должна входить в МДНФ. Совокупность таких импликант образует ядро МДНФ. (Вы не путаете ДНФ с КНФ?)

Совокупность элементарных импликант, которые входят в любую минимальную дизъюнктивную нормальную форму, называется ядром этой формы.

В рассматриваемом примере ядром является формула:

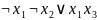
Те столбцы, в которых импликанты из ядра уже дают 0, можно не учитывать в дальнейшем, т. к. импликанты из ядра уже «перекрывают» соответствующие полные наборы значений переменных, на которых функция имеет значение 0.

Действительно, я перепутала в этом примере СДНФ и СКНФ.

Рассмотрим булеву функцию f, заданную равенствами:

f (0,0,0) = f (0,0,1) = f (1,0,1) = f (1,1,1) = 0

x	y	z	f
0	0	0	0
0	0	1	0
0	1	0	1
0	1	1	1
1	0	0	1
1	0	1	0
1	1	0	1
1	1	1	0

Для этой функции СДНФ является выражение:

(¬X∧Y∧¬Z) ∨(¬X∧Y∧Z) ∨(X∧¬Y∧¬Z) ∨(X∧Y∧¬Z)

Проводя сокращения по законам логики, получим тупиковую ДНФ:

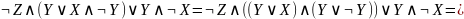
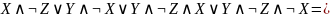
После этого построим таблицу, в которую запишем те строки, результат которых равен 1:

X	Y	Z	f
0	1	0	1
0	1	1	1
1	0	0	1
1	1	0	1

Теперь будем проводить операцию склеивания. Склеивание производим до тех пор, пока это возможно:

		Импликанты 1‑го уровня
0 1 0 1 0 0 0 1 1 1 1 0	0 1 0 = > 0 1 _ 0 1 1 0 1 0 = > _ 1 0 1 1 0 1 0 0 = > 1 _ 0 1 1 0	0 1 _ _ 1 0 1 _ 0

Составим таблицу (Квайна), показывающую соответствие элементарных импликант и наборов значений переменных функции по значениям 0 данной функции:

Элементарные импликанты	Сокращенные наборы	Наборы значений переменных, определяющие 1 булевой функции
		0 1 0	0 1 1	1 0 0	1 1 0
	0 1 _	1	1
	_ 1 0	1			1
	1 _ 0			1	1

Теперь найдем дизъюнктивное ядро. Для этого необходимо найти те столбцы, в которых присутствует только один символ "1". Они составят наше дизъюнктивное ядро:

01_

1_0

Функция будет состоять только из импликантов дизъюнктивного ядра: 01_ ∨ 1_0

Теперь, заменяя 1 на соответствующую переменную, а 0 - на отрицание этой переменной (символ "-" вообще в расчет не берем, просто игнорируя его), получаем упрощенную функцию: ¬X∧Y ∨ X∧¬Z

(Как ядро расширяется до МДНФ?)

Члены сокращённой формы, не подлежащие исключению, образуют ядро. Для каждой из них имеется хотя бы один столбец, перекрываемый только этим членом.

Для получения минимальной формы достаточно выбрать из членов сокращённой формы, не входящих в ядро, такое минимальное их число с минимальным количеством букв в каждом из этих членов, которое обеспечит перекрытие всех столбцов, не перекрытых членами ядра.

б) Рассмотрим булеву функцию f, заданную равенствами:

f (0,0,0) = f (0,0,1) = f (1,0,0) = f (1,1,0) = f (1,1,1) = 1

Для этой функции СДНФ является выражение:

(Поясните как получили.) (Где пояснения?)

Ниже приводится исправление.

Проводя сокращения по законам логики, получим тупиковую ДНФ:

Получим следующие наборы с прочерками, которые больше не сокращаются: (1,1,_)(_,1,1)(0,_,1)(0,0,_) (Проверьте по исходным наборам. Укажите какие наборы «склеиваются». Учитывайте порядок.)

Составим таблицу (Квайна), показывающую соответствие элементарных импликант и наборов значений переменных функции по значениям 1 данной функции:

Элементарные импликанты	Сокращенные наборы	Наборы значений переменных, определяющие 0 булевой функции
		000	001	100	110	111
	00_	1	1
	_00	1		1
	1_0			1	1
	11_				1	1

В рассматриваемом примере ядром является формула:

Для «перекрытия» полного набора переменных достаточно выбрать одну из соответствующих элементарных импликант выделенном столбце. Поэтому получаем две различные минимальные дизъюнктивные нормальные формы:

1. 

2. 

Этот пример показывает, что минимальная ДНФ не всегда является наименьшей, которая по определению должна быть единственной.

Исправление: рассмотрим булеву функцию f, заданную равенствами:

f (0,0,0) = f (0,0,1) = f (1,0,0) = f (1,1,0) = f (1,1,1) = 1

Для этой функции СДНФ является выражение:

x	y	z	F(x,y,z)
0	0	0	1
0	0	1	1
0	1	0
0	1	1
1	0	0	1
1	0	1
1	1	0	1
1	1	1	1

Выбираем все строчки, где функция равна 1:

1)x=y=z=0. Тогда элементарная конъюнкция имеет вид:

2)x=y=0, z=1. Тогда элементарная конъюнкция имеет вид:

3)y=z=0, x=1. Тогда элементарная конъюнкция имеет вид:

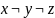
4)x=y=1, z=0. Тогда элементарная конъюнкция имеет вид:

5)x=y=z=1. Тогда элементарная конъюнкция имеет вид

Получаем:

Проводя сокращения по законам логики, получим тупиковую ДНФ:

x

∧

¬

z

∨

x

∧

y

∨

¬

x

∧

¬

y

Теперь будем проводить операцию склеивания. Склеивание производим до тех пор, пока это возможно:

		Импликанты 1‑го уровня
0 0 0 0 0 1 1 0 0 1 1 0 1 1 1	0 0 0 = > 0 0 _ 0 0 1 0 0 0 = > _0 0 1 0 0 1 0 0 = > 1 _ 0 1 1 0 1 1 0 = > 1 1 _ 1 1 1	0 0 _ _0 0 1 _ 0 1 1 _