
ЛР_2
.docxМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное образовательное
учреждение высшего образования
«Юго-Западный государственный университет»
Лабораторная работа №2
По дисциплине «Математическая логика и теория алгоритмов»
Вариант №5
Выполнил: Бунина А.В.
студент группы ИБ-01б
Проверил: Добрица В.П.
профессор
Курск, 2021
Задача 1. Среди данных формул указать ДНФ. 1) (A∧B)∨(С∧¬D); 2) (A∨B) ∧ (C∨D); 3) (A∧B)∨(A|C); 4) (А∨C)∧(A∨¬В∨¬C); 5) (А∧В∧C)∨(A∧¬B∧¬C) .
Дизъюнктивной нормальной формой (ДНФ) называется произвольная дизъюнкция элементарных конъюнкций. Мы видим сразу, что вариант 2,4 не подходит (это КНФ - произвольная конъюнкция элементарных дизъюнкций), а вариант 3 имеет штрих Шеффера.
Ответ: 1, 5.
(Что такое элементарная конъюнкция?)
Элементарная конъюнкция – формула, содержащая конъюнкцию отдельных элементарных высказываний, которые могут быть с отрицанием, и каждая переменная встречается не более одного раза.
Задача 2. Выразить функцию X|Y через импликацию и отрицание.
(Опирайтесь на законы логики.)

Задача 3. Приведите данные логические выражения к конъюнктивной и дизъюнктивной нормальной формам (КНФ и ДНФ). Докажите равносильность полученных формул.
• (Х | У) → (У ∼¬Z);
• (Х ∼¬У) | (Z →¬У).
ДНФ (Х | Y) → (Y
∼ Z):
Z):
 (Откуда взялась 1?)
(Откуда взялась 1?)
(Здесь уже применяете выражение штриха Шеффера, а в предыдущей задаче этого не сделали? Осталось только конъюнкцию выразить через импликацию.)
ДНФ (Х | Y) → (Y
∼
Z):

Доказать равносильность полученных формул можно при помощи таблицы истинности:
X |
Y |
Z |
X↑Y |
|
|
|
X↑Y→( ) |
ДНФ |
КНФ |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
|
ДНФ (Х ∼¬У) |
(Z →¬У):

Доказать равносильность полученных формул можно при помощи таблицы истинности:
X |
Y |
Z |
|
|
Z→ |
X |
ДНФ |
КНФ |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
|
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
|
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
|
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
|
Задача 4. Построить СКНФ от трех переменных, которая равна 0 тогда и только тогда, когда одна или три переменные равны 1.
A |
B |
C |
F |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
В таблице истинности нужно выбрать строки, где F = 0. При записи СКНФ нужно записать дизъюнкцию переменных, равных 0. Когда переменная равна 1, то она становится отрицательной. (Наверное берется в дизъюнкции с отрицанием?)
F(A,B,C) = (A∨B∨¬C) ∧(A∨¬B∨C) ∧ (¬A∨B∨C) ∧ (¬A∨¬B∨¬C)
В таблице истинности нужно выбрать строки, где F = 0. При записи СКНФ нужно записать дизъюнкцию переменных, равных 0. Когда переменная равна 1, то она берется в дизъюнкции с отрицанием.
Задача 5. Построить формулу алгебры высказываний, обладающую следующей функцией истинности: f(0,0,0)=f(1,1,0)=f(0,1,0)=f(0,1,1)=1
x |
y |
z |
F(x,y,z) |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
Составим СДНФ: (¬x∧¬y∧¬z) ∨ (¬x∧y∧¬z) ∨ (¬x∧y∧z) ∨ (x∧y∧¬z)
Ответ: f(x,y,z)= (¬x∧¬y∧¬z) ∨ (¬x∧y∧¬z) ∨ (¬x∧y∧z) ∨ (x∧y∧¬z)
(Опишите алгоритм построения.)
Выбираем все строчки, где функция равна 1:
x=y=z=0. Тогда элементарная конъюнкция имеет вид: (¬x∧¬y∧¬z)
x=z=0, y=1. Тогда элементарная конъюнкция имеет вид: (¬x∧y∧¬z)
y=z=1, x=0. Тогда элементарная конъюнкция имеет вид: (¬x∧y∧z)
x=y=1, z=0. Тогда элементарная конъюнкция имеет вид: (x∧y∧¬z)

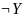
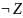

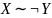
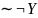 ↑(Z→
)
↑(Z→
)