
Физика лекции (понятные)
.pdf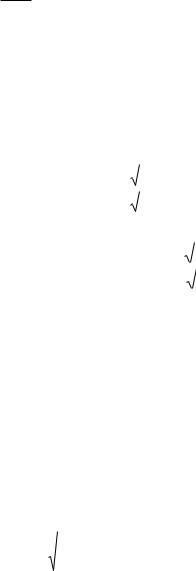
12
Из условия непрерывности |
Ψ и |
|
в точке |
х = 0 |
следует, что |
||||||||||||
х |
|||||||||||||||||
1 0 2 0 |
|
|
|
|
|
|
|
|
|
||||||||
или |
А1 В1 А2 |
|
и |
|
|||||||||||||
1 |
0 |
2 |
0 |
или |
A k B k |
A k |
|
||||||||||
х |
|
|
|
|
х |
|
|
|
1 |
1 |
1 |
1 |
2 |
2 |
|||
|
|
|
|
|
|
|
|
|
|||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B1 k1 k2 |
|
и |
A2 |
|
2k1 |
|
|
|
|||||||
|
|
A1 |
|
|
k1 k2 |
|
A1 |
|
|
k1 k2 |
|
|
|||||
|
|
|
|
|
|
|
|
||||||||||
Для определения коэффициентов R |
и |
|
D вводят понятие плотности |
||||||||||||||
потока вероятности |
|
j , |
|
вектор которого определяется через волновую |
|||||||||||||
функцию следующим образом: |
grad |
grad |
|
||||||||||||||
|
|
j |
|
i |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2m0
В соответствии с видом Ψ-функции для падающей, отражённой и прошедшей волн имеем:
jпад ~ k1A12 |
|
, |
|
|
jотр ~ k1B12 |
|
и |
jпрош ~ k2A22 |
|
|||||||||||||||||||||||||
Теперь можно записать |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
для коэффициента отражения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||
|
|
|
|
|
j |
ОТР |
|
|
|
В |
|
|
1 |
1 U 0 / E |
|
|
|
|
||||||||||||||||
|
|
R |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
jПАД |
|
|
|
А1 |
|
|
|
|
|
1 |
1 U |
0 / E |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
для коэффициента пропускания |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
D |
j |
ПРОШ |
k |
2 |
|
|
A |
|
|
|
4k k |
2 |
|
|
4 1 U 0 / E |
|
||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k1 |
k |
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
||||
|
|
jПАД |
|
|
|
|
|
|
|
|
|
|
|
(1 1 U |
0 / E ) |
|||||||||||||||||||
|
|
k1 |
|
A1 |
|
|
|
2 |
|
|
|
|||||||||||||||||||||||
Видно, что R + D = 1 , что и должно быть по определению. Коэффициенты R и D не зависят от направления движения частицы: слева направо или наоборот.
В классическом случае при E > U0 должно быть R = 0.
Эффект надбарьерного отражения ( R > O ) является чисто квантовым и объясняется наличием у частицы волновых свойств.
2). Высокий порог ( E < U0 ). |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
В этом случае |
k2 |
|
2m0 |
E U 0 |
является чисто мнимым. |
|||||||
|
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||
Коэффициент отражения |
R |
|
k |
|
k |
|
|
2 |
1 т.к. числитель и знаменатель – |
|||
|
|
|
||||||||||
|
k |
1 |
k |
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
величины комплексно-сопряжённые. Таким образом, отражение будет полным, а D = 0.

13
Но волновая функция при x > 0 не обращается в нуль, т.е. микрочастицы могут проникать в области, которые для макроскопических
частиц недоступны. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Плотность |
вероятности нахождения |
частицы |
в |
области |
|
II |
|||||||||||||||
определяется выражением |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
P |
|
|
|
2 |
|
|
2k |
|
|
2 |
4k 2 |
|
|
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
w2 x 0 |
|
2 |
x |
|
|
|
|
exp 2k2 x |
|
|
2m0 U0 E |
|
||||||||||
|
|
|
1 |
|
|
2 |
2 exp |
|
|
x |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
k1 ik2 |
|
|
|
k1 k2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
и зависит от массы |
|
т0 |
, разности ( U0 – E ) |
и расстояния от границы |
||||||||||||||||||
порога. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для |
электрона |
с |
(U0 – E) = 1 эВ |
вероятность нахождения |
|
на |
|||||||||||||||
расстоянии от порога сравнимым с размерами атома |
|
( х = 10-10 м ) |
||||||||||||||||||||
достаточно велика, а на расстоянии в 10 раз большем |
( х = 10-9 м ) ничтожно |
|||||||||||||||||||||
мала. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отражение хотя и является полным |
(R |
= |
1) не обязательно |
|
|||||||||||||||||
происходит на самом пороге. Частица может проникнуть в область II , а затем выйти из неё ( аналогично полному внутреннему отражению в оптике).
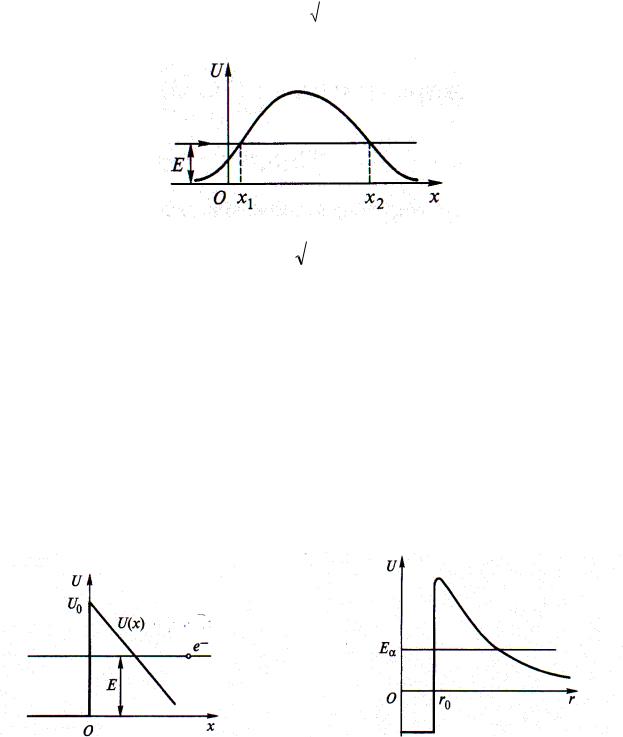
Прохождение частицы через потенциальный барьер.
Рассмотрим одномерный прямоугольный потенциальный барьер
Частица движется слева направо. Слева от барьера имеем падающую и отраженную волну, а за барьером только прошедшую волну.
Уравнение Шрёдингера для областей |
|
I, II |
и III имеет вид: |
|||||||||||
|
|
2 |
х |
k1 |
2 |
1 x 0 |
|
|
|
|||||
|
|
1 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
х2 |
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
x |
k2 |
2 |
2 |
x 0 |
|
|
|
||||
|
|
2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
x2 |
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
x |
k1 |
2 |
3 x 0 |
|
|
|
|||||
|
|
3 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
x2 |
|
|
|
|
|
|
|
|
|
|||
Где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
k1 |
2m0 E |
|
|
, k2 |
|
|
2m0 U |
0 E |
||||||
2 |
|
|
|
|
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||
Волновые функции, являющиеся решением этих уравнений |
||||||||||||||
|
|
х А eik1x B e ik1x |
|
|
|
|||||||||
|
|
1 |
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
x |
A ek2 x B e k2 x |
|
|
|
||||||||
|
|
2 |
|
|
|
|
2 |
|
|
2 |
|
|
|
|
14
3 x A3eik1x B3e ik1x
Из решения этой системы уравнений получают, применив некоторые упрощающие допущения, выражение для коэффициента прозрачности D прямоугольного барьера
|
|
2a |
|
|
|
|
|
|
|
D exp |
|
2m |
U |
0 |
E |
||||
|
|||||||||
|
|
|
0 |
|
|
|
|||
|
|
|
|
|
|
|
|
||
Для потенциального барьера произвольной формы
|
|
|
|
2 |
x2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
D exp |
|
|
|
2m |
U x E |
dx |
|
||||
|
||||||||||||
|
|
|
|
0 |
|
|
|
|||||
|
|
|
|
x1 |
|
|
|
|
|
|
||
Пределы интегрирования |
|
|
х1 |
|
и |
х2 |
определяют из решения |
|||||
уравнения U( x ) = E .
Туннельный эффект
Прохождение частицы через потенциальный барьер, высота которого превышает энергию частицы, получило название туннельного эффекта (частица, проходя под барьером, как бы движется в туннеле). При прохождении через барьер полная энергия частицы Е не меняется.
Туннельный эффект представляет собой чисто квантовое явление. Этим эффектом объясняются многие физические явления; например,
холодная эмиссия электронов из металла (автоэмиссия), альфа-распад, спонтанное деление ядер и др.
На левом рисунке представлен потенциальный барьер треугольной формы, имеющий место на границе металл-вакуум в явлении холодной эмиссии электронов из металла. Электрон в металле находится в
потенциальной яме глубиной U0 . Если вблизи поверхности металла
имеется электрическое поле напряжённостью Е , способствующее выходу электронов из металла, то потенциальная энергия электрона вблизи поверхности металла может быть представлена в виде

15
U x U0 e E x
При туннелировании электронов через этот барьер происходит их выход из металла даже при низких температурах.
На правом рисунке представлен потенциальный барьер α-частицы в поле ядра. На больших расстояниях r между α-частицей и ядром действуют силы кулоновского отталкивания и потенциальная энергия частицы
|
|
|
U r |
1 |
|
Ze 2e |
, |
где |
|
|
|
|
|
4 0 |
|
||||
|
|
|
|
|
|
r |
|
||
Ze – заряд дочернего ядра; |
2е – заряд α-частицы. |
||||||||
Внутри ядра |
(r |
< r0 ) |
α-частица находится в потенциальной яме, |
||||||
выйти из которой она может только за счёт туннельного эффекта. |
|||||||||
Прохождение частицы над барьером |
( E > U0 ) |
||||||||
Частица массой |
т0 |
падает на прямоугольный потенциальный барьер |
|||||||
высотой U0 и шириной |
а . Энергия частицы Е больше высоты барьера. |
||||||||
В этом случае решение системы уравнений Шрёдингера для трёх |
|||||||||
областей: I – ( x < |
0 ), II – ( 0 < x < a ), |
III – ( x > a ) даёт следующие |
|||||||
значения для коэффициента прохождения D . |
|
|
|
|
1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
U0 |
|
|
|
|
2m0 |
E U |
0 |
|
||||||||
D 1 |
|
|
|
sin2 a |
|
|
|||||||||||
4E E U0 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Частица беспрепятственно проходит над таким барьером ( D = 1 ) при |
|||||||||||||||||
значениях энергии равных |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
E |
2 2 |
n2 U |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
0 |
, |
где n = 1, 2, 3, … |
( sin = 0 ) |
||||||||||||
2m a2 |
|||||||||||||||||
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При других значениях энергии существует отличная от нуля вероятность отражения частицы от барьера.
Пролёт частицы над потенциальной ямой конечной глубины ( E >
U0 )
Частица пролетает над потенциальной ямой конечной глубины U0 и ширины а слева направо вдоль оси ох.

16
Решая систему уравнений Шрёдингера для трёх областей, получаем выражение для коэффициента прохождения D , характеризующего вероятность прохождения частицы над ямой:
|
|
|
|
|
|
|
|
|
1 |
|||
|
U |
0 |
|
|
|
2m E |
||||||
D 1 |
|
|
|
|
sin 2 a |
|
0 |
|
|
|||
4E E U 0 |
|
|
|
|||||||||
|
|
|
|
2 |
|
|
|
|||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||
Коэффициент прохождения D зависит от соотношения между энергией частицы и глубиной потенциальной ямы и в общем случае оказывается меньше единицы (частица может отразится от потенциальной ямы даже если E > U0 ). Данное явление, полностью отсутствующее в
классической физике, объясняется наличием у частицы волновых свойств.
Частица не испытывает отражения на границах ямы ( D = 1 ) только если sin = 0 . Это условие выполняется при значениях энергии частицы
E |
2 |
2 |
U0 , где n = 1, 2, 3, … |
||
|
|
|
n2 |
||
2m a |
2 |
||||
|
0 |
|
|
|
|
Рассмотренная модель поведения частицы вблизи симметричной прямоугольной потенциальной ямы конечной глубины хорошо качественно описывает движение электрона вблизи атома. В частности, проведённый анализ даёт квантово-механическое объяснение эффекта Рамзауэра, где наблюдалась аномальная прозрачность атомов инертных газов для пучка электронов при определённых значениях кинетической энергии (K = E – U0).
|
|
|
|
|
|
|
|
Б |
|
Условие а |
2т0 |
Е |
|
n |
можно представить в виде |
a |
п |
||
2 |
|
2 |
|||||||
|
|
|
|
|
|
|
|
||
(λБ – длина волны де Бройля электрона внутри ямы ). Это условие определяет гашение за счёт интерференции волн, отражённых от двух границ ямы аналогично просветлению оптики при интерференции двух электромагнитных волн от двух сторон просветляющей тонкой плёнки.
КОШКА ШРЁДИНГЕРА
Кошка ( или кот ) Шрёдингера – герой кажущегося парадоксальным мысленного эксперимента Эрвина Шрёдингера, которым он хотел продемонстрировать неполноту квантовой механики при переходе от субатомных систем к макроскопическим.
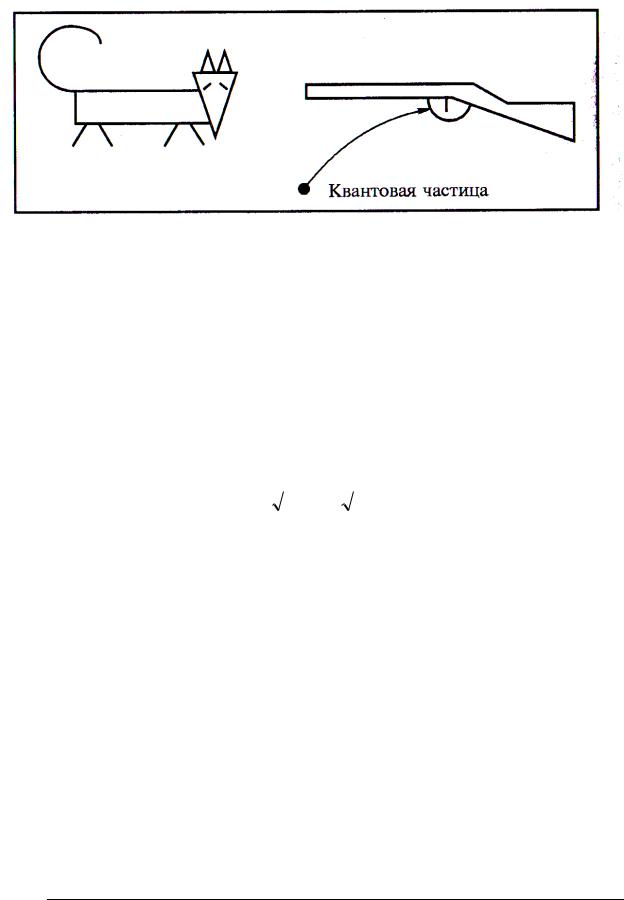
17
Кошка помещена в закрытый ящик, где на неё направлен ствол ружья. В ящике находится также микрочастица, при попадании которой в курок ружья, ружьё стреляет и кошка погибает.
Если частица находится в первом квантовом состоянии, описываемом волновой функцией Ψ1 , в котором вероятность обнаружить частицу в области вблизи курка равна нулю, то кошка в ящике жива.
Пусть в состоянии Ψ2 вероятность нахождения частицы вблизи курка равна единице. В этом случае кошка мертва.
Согласно принципу суперпозиции
|
1 |
|
|
1 |
|
|||
|
|
|
|
|
||||
|
2 |
1 |
2 |
2 |
||||
|
|
|
|
|
||||
И непонятно жива или мертва кошка?
Системы, в которых формально объединены как классические так и квантовые объекты не всегда корректны для исследования.
Лекция 7
Операторы физических величин
Ранее было сказано, что состояние квантовой частицы определяется не координатами и импульсом, а заданием Ψ-функции, вид которой зависит от конкретного потенциального поля ( 1-ый постулат квантовой механики ). Волновая функция, описывающая сама по себе распределение по координатам, определяет также распределение по импульсам и другим динамическим характеристикам частицы, таким как кинетическая энергия, момент импульса и др.
Таким образом Ψ-функция полностью определяет не только «положение» частицы, но и все её динамические характеристики.
Для получения информации о физических величинах, связанных с движущейся частицей, в квантовой механике разработан специальный
математический аппарат, в котором используют операторы физических величин и результаты их действия на волновую функцию.
18
Оператором называют символическое обозначение математической операции, которую необходимо совершить с интересующей нас функцией. Примером оператора могут служить умножение на х , или на какую-либо
функцию |
f(x), |
дифференцирование |
по |
х |
т.е. |
|
|
|
; |
|
|
2 |
|
, |
операторы |
|||||||||||||||||
|
х |
|
х 2 |
|||||||||||||||||||||||||||||
набла - , лапласиан - |
2 и т.д. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
В |
квантовой |
механике |
операторы принято |
обозначать |
|
буквами со |
|||||||||||||||||||||||||
«шляпкой», например , |
ˆ |
а его действие на некоторую функцию |
|
f( x ) |
||||||||||||||||||||||||||||
Q , |
|
|||||||||||||||||||||||||||||||
записывают как |
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Qf x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Некоторые свойства операторов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
1). Операторы можно складывать: |
|
ˆ |
|
ˆ |
|
|
. |
Действие |
|
такого |
|||||||||||||||||||||
|
|
А В |
|
|
|
|||||||||||||||||||||||||||
суммарного оператора на любую функцию |
f( x) |
|
даёт результат |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ˆ |
ˆ |
|
|
ˆ |
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
В f x |
Af x Bf x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2). Под произведением операторов |
|
|
ˆ |
ˆ |
|
|
|
понимают |
оператор, |
||||||||||||||||||||||
|
|
|
АВ |
|
|
|
||||||||||||||||||||||||||
результат действия которого на любую функцию |
f(x) |
равен |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ˆ ˆ |
|
|
ˆ ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
АВ f x A Bf x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Т.е. функция f(x) |
сначала подвергается действию оператора |
|
|
ˆ |
|
а затем |
||||||||||||||||||||||||||
|
В , |
|
||||||||||||||||||||||||||||||
полученный результат – действию оператора |
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
А . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Следует иметь ввиду, что не всегда |
ˆ |
ˆ |
|
ˆ ˆ |
|
|
|
Если такое равенство |
|||||||||||||||||||||||
|
АВ |
ВА . |
|
|||||||||||||||||||||||||||||
соблюдается, то это значит, что операторы |
ˆ |
|
и |
|
ˆ |
|
коммутируют друг с |
|||||||||||||||||||||||||
А |
|
|
В |
|
||||||||||||||||||||||||||||
другом |
(коммутирующие операторы ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Пример некоммутирующих операторов – это |
х |
и |
|
: |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|||
|
|
|
|
|
f |
|
|
|
|
|
|
|
xf |
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x |
|
f |
x |
|
, |
а |
|
|
|
x f |
|
|
f x |
|
|
|
|
|
|
|
|
х |
|
|
|
|
х . |
|||||
|
x |
x |
|
x |
x |
|
|
|
|
|
|
|
х |
х |
||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
3). Оператор |
ˆ |
называют линейным, если для любых двух функций |
|||||||||||||||||||||||||||||
|
А |
|||||||||||||||||||||||||||||||
f1 и |
|
f2 |
и любых постоянных |
а1 |
|
и |
а2 выполняется соотношение |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
ˆ |
|
|
a2 f |
|
|
ˆ |
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A a1 f1 |
2 a1 Af1 |
a2 Af2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
С линейностью операторов связан принцип суперпозиции состояний. |
|||||||||||||||||||||||||||||||
|
Оператором |
физической |
величины |
может |
быть |
только |
линейный |
|||||||||||||||||||||||||
самосопряжённый (эрмитов) оператор. Самосопряжённым называют оператор, который совпадает со своим сопряжённым оператором. В этом
случае для произвольных функций 1 |
и |
2 |
тождественно выполняется |
|||||
следующее интегральное равенство |
|
|
|
|
|
|||
|
|
|
ˆ |
|
f |
ˆ |
|
)dV |
|
f1 |
( А f2 )dV |
2 ( Af1 |
|||||
|
V |
|
|
|
V |
|
|
|
ˆ |
ˆ |
то |
ˆ |
ˆ |
|
|
|
|
4). Если Af |
Bf |
A B . |
|
|
|
|||
Представление физических величин операторами в квантовой механике
19
Второй постулат квантовой механики – каждой физической величине соответствует определённый линейный эрмитов оператор этой физической величины. При этом соотношения между операторами в квантовой механике имеют ту же структуру, что и соотношения между соответствующими им физическими величинами в классической механике.
1. Оператор координаты
ˆ |
|
x |
ˆ |
|
y ; |
zˆ |
|
z . |
x |
|
; y |
|
|
||||
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
r |
ex xˆ |
ey yˆ |
ez zˆ . |
|
||
2. Оператор импульса
ˆ |
i |
|
; |
pˆ y i |
|
|
; |
pˆ z |
i |
|
; |
||||||
|
|
|
|
||||||||||||||
рх |
x |
y |
|
z |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p i i e |
x |
|
e |
y |
|
|
e |
z |
|
|
|
|
||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
x |
|
|
|
y |
|
|
. |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|||
3. Оператор квадрата импульса
pˆ 2 pˆ |
|
2 pˆ |
|
2 pˆ 2 |
|
|
2 |
|
|
2 |
|
|
|
|
||
|
|
2 2 2 |
|
|
||||||||||||
|
x |
|
y |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
y |
2 |
|
z |
2 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4. Оператор момента импульса
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
ex |
ey |
ez |
|
|
|
|
|
|||||
|
|
|
L |
r; р = |
x |
|
|
y |
z |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
px |
p y |
pz |
|
|
|
|||||||
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
L |
x |
|
ypˆ |
z |
zpˆ |
y |
i y |
|
|
|
|
z |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
||||||
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
ˆ |
|
|
ˆ |
|
|
i z |
|
|
|
|
|
x |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Ly |
zpx |
xpz |
|
x |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
||||||||
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
L |
z |
xpˆ |
y |
ypˆ |
x |
i x |
|
|
|
|
|
|
y |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
||||||||
В сферической системе координат (r, , )
ˆ |
|
|
|
|
|
|
|
|
|
|
||||
L |
x |
i sin |
|
|
|
|
ctg cos |
|
|
|
|
|||
|
|
|
|
|
|
|
|
, |
||||||
|
|
|
|
|
|
|
|
|||||||
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
y |
i cos |
|
|
|
|
ctg sin |
|
|
|
|
, |
||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
|
ˆ |
i |
|
|
|
|
|
|
Lz |
|
. |
|
|||
|
|
|
|
|
|
||
5. Оператор квадрата момента импульса |
|
|
|||||
ˆ2 |
ˆ |
ˆ |
ˆ ˆ |
|
ˆ |
ˆ |
|
L |
Lx Lx |
Ly Ly |
Lz |
Lz |
|||
В cферической системе координат ( r, θ, φ )
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
ˆ2 |
|
2 |
|
2 |
|
||
|
|
|
|
|
|
|
|
|
L |
|
, |
, где |
|||||
|
2 |
|
1 |
|
|
|
|
|
1 2 |
|
|
||||||
|
|
, |
|
|
|
sin |
|
|
|
|
|
|
|
|
|
- |
угловая часть оператора Лапласа |
|
|
|
|
|
sin 2 |
|
|||||||||||
|
|
|
sin |
|
|
2 |
|
|
|||||||||
всферической системе координат.
6.Операторы энергий
|
|
|
|
|
|
|
|
|
|
|
|
К |
т 2 |
|
p 2 |
|||
Кинетическая энергия в классической механике |
0 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|||||||||||||
|
2 |
|
2m0 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
В соответствии со вторым постулатом получаем |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
ˆ |
рˆ 2 |
2 |
2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
К |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
2т0 |
2т0 |
|
|
|
|
|
|
|
|
|
||
Для потенциальной энергии |
в стационарном силовом |
поле |
U |
kx2 |
|
|||||||||||||
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||
|
ˆ |
k |
2 |
kx2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
получаем: |
|
xˆ |
|
U . Это определение |
ˆ |
|
|
|
|
|
|
|||||||
U |
2 |
2 |
U U справедливо не |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
только для гармонического осциллятора но о в общем случае для частицы, движущейся в стационарном силовом поле, где её потенциальная энергия U U (x, y, z) определена в любой точке пространства.
Оператор полной энергии
|
ˆ ˆ |
ˆ |
2 |
2 |
U x, y, z |
||
|
H K U |
2m0 |
|
|
|||
|
|
|
|
|
|
||
Этот оператор называют |
оператором |
|
функции Гамильтона или |
||||
гамильтонианом, который является основным оператором квантовой механики, определяющим все особенности квантовой системы.
Уравнение Шрёдингера в операторной форме принимает вид:
ˆ |
|
Временное – H i |
t |
|
Для стационарных состояний – ˆ Е
Н
Собственные функции и собственные значения операторов
Состояние, в котором физическая величина Q имеет определённое значение ( так называемое собственное состояние ), описывается Ψ- функцией, являющейся решением уравнения
ˆ
Q Q
Примером такого уравнения является уравнение Шрёдингера для стационарного состояния.
21
Физический смысл могут иметь лишь такие решения этого уравнения, которые всюду конечные, однозначные, непрерывные и гладкие. Эти условия называются естественными или стандартными.
Функции, |
являющиеся |
решением |
данного |
уравнения |
и |
|
удовлетворяющие |
естественным |
условиям |
называются |
собственными |
||
функциями оператора |
ˆ |
|
|
|
|
|
Q . |
|
|
|
|
||
Те значения величины Q , при которых эти решения существуют, называются собственными значениями физической величины Q , например, собственные значения энергий в потенциальных ямах.
Набор (спектр) собственных значений физической величины Q иногда оказывается непрерывным, а иногда дискретным. Примером дискретности в микромире являются оптические спектры атомов, которые состоят из ряда отдельных тонких линий.
Рассмотрим несколько задач о нахождении спектров собственных
значений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1). Координата х |
и х ; |
|
|
|
|
|
|
|
|||||||
хˆ х |
|
хˆ х |
т.е. |
спектр непрерывный. |
|||||||||||
2). Проекция импульса рх |
|
|
|
|
|
|
|
|
|
|
|
||||
|
ˆ |
|
|
|
|
|
|
|
|
|
|
px |
|
||
|
|
i |
|
|
px |
|
C exp i |
|
|
x |
|||||
|
рх рх |
|
x |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Функция |
Ψ |
определена при всех значениях |
рх |
т.е. спектр собственных |
|||||||||||
значений |
рх |
непрерывен |
( рх ; ). |
|
|
|
|
|
|
|
|||||
3). Проекция момента импульса |
Lz |
|
|
|
|
|
|
|
|||||||
|
ˆ |
|
|
|
|
|
|
|
|
|
|
Lz |
|
|
|
|
Lz Lz |
i |
|
Lz |
|
C exp i |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Собственные |
функции оператора |
|
ˆ |
должны быть |
однозначными |
||||||||||
|
Lz |
||||||||||||||
функциями. Так как |
угловая координата |
|
φ |
является циклической |
|||||||||||
переменной, то условие однозначности собственной функции сводится к условию её периодичности :
|
|
Lz 2 |
|
|
|
Lz |
|
|
|
Lz 2 |
|
|
Lz |
2 |
|
||||||
Тогда |
exp i |
|
|
|
exp i |
|
|
|
|
exp i |
|
1 |
|
|
|
2 m , |
|||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где |
m 0, 1, 2, 3,... Следовательно спектр дискретный. |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
С exp im |
1 |
exp im |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
т |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Значение константы |
C |
|
1 |
|
выбрано из условия нормировки |
|
||||||||||||||
|
|
2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
m d 1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|||||
0
