Сложение векторов.

С уммой двух векторов и называется вектор , соединяющий начало вектора с концом вектора , отложенного от конца вектора .

Произведение вектора на число.

Произведение м вектора на число называется вектор, который имеет длину и который имеет направление вектора в случае и противоположное направление в случае .

Пример 3.1. Даны векторы и .

П остройте векторы: 1) ;

2) .

§ 2. Декартовы прямоугольные координаты вектора. Длина вектора.

Пусть вектор составляет угол с осью .

П роекцией вектора на ось называется число, равное длине вектора (рис.3.1), взятой со знаком «плюс», если направление вектора совпадает с направлением оси и со знаком «минус» в противном случае.

П роекцию вектора на ось можно вычислить по формуле:

.

Д екартовыми прямоугольными координатами вектора называются его проекции на соответствующие координатные оси .

В ектор с координатами записывают в виде или , где — единичные векторы координатных осей соответственно. Длина вектора определяется по формуле:

.

Если вектор задан точками и , то его координаты вычисляются по формулам:

.

Пример 3.2. Даны две точки и . Найдите координаты и длину вектора .

П о условию задачи , , , , , . Значит, .

.

Пример 3.3. Даны два вектора и . Найдите координаты и длину вектора .

; ;

;

.

С овместим параллельным переносом начало некоторого вектора с началом координат прямоугольной системы координат . Пусть — углы, которые образует вектор с осями координат соответственно (рис.3.2). Направление вектора определяется с помощью направляющих косинусов , , , для которых справедливы равенства:

, .

§ 3. Скалярное произведение векторов.

С калярным произведением двух ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла между ними (см. рис.3.3):

.

И з рис. 3.3 видно, что .

Поэтому или . (*)

Свойства скалярного произведения.

1. — переместительный закон.

2. — распределительный закон.

3. Е сли то .

4. (или или ).

В частности, скалярное произведение единичных векторов (ортов) удовлетворяет равенствам:

5. Е сли векторы заданы координатами , 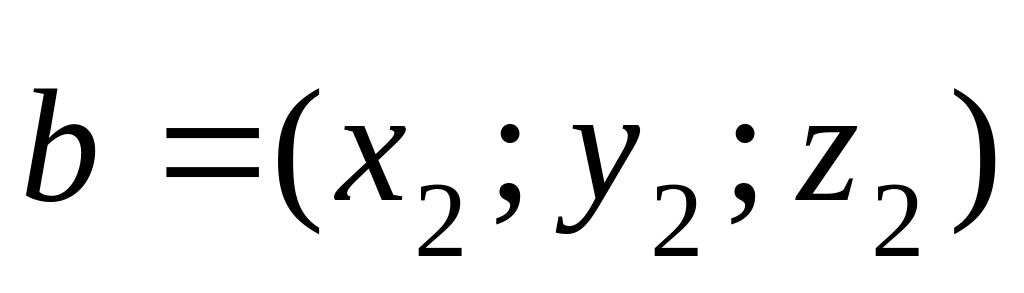или , , то

.

6. У гол между векторами и определяется по формуле:

.

1. В екторы и коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны, т.е.:

.

2. У словие перпендикулярности векторов и :

.

Пример 3.4. Векторы и образуют угол . Зная, что и , вычислите .

.

П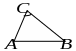 ример 3.5. Даны вершины треугольника , и . Найдите: 1) внутренний угол при вершине ;

2) .

Д ля нахождения угла найдём векторы и .

;

.

Тогда Т.е.

Согласно формуле (*)

.

ЧТО ДОЛЖЕН ЗНАТЬ СТУДЕНТ

1. Понятие вектора.

2. Понятие единичного и нулевого вектора.

3. Модуль вектора, формула расстояния между двумя точками.

4. Понятие коллинеарности векторов.

5. Линейные операции над векторами.

6. Понятие проекции вектора на ось.

7. Скалярное произведение векторов.