§ 8. Экстремум функции двух переменных
Максимумом
(минимумом)
функции
в точке M0(x0,y0)
называется такое ее значение
,
которое
больше (меньше) всех других ее значений,
принимаемых в точках
,
достаточно близких к точке
и отличных от нее.
Точки максимума и минимума называют точками экстремума,а значения функции в этих точках называются экстремальными.
Необходимые
условия экстремума.
Если
дифференцируемая функция
имеет экстремум в точке
,
то ее частные производные в этой точке
равны
нулю, т.е.
.
Точки,
в которых
и
,
называются стационарными
точками
функции
.
Достаточные
условия экстремума.
Пусть
является стационарной точкой функции
и пусть
,
,
.
Составим определитель
.
Тогда:
если
,
то в стационарной точке
нет экстремума;
если
,
то в точке
есть экстремум, причем максимум, если
А
< 0,
минимум,
если
;
если
,
то требуется дополнительное исследование.
Пример
8.10.
Исследовать на экстремум функцию
.
Н
аходим
частные производные первого порядка:
;
Решая систему уравнений
получаем
две стационарные точки:
и
.
Находим частные производные второго порядка:
,
,
.
Исследуем каждую стационарную точку.
В точке имеем:
,
,
.
Тогда
.
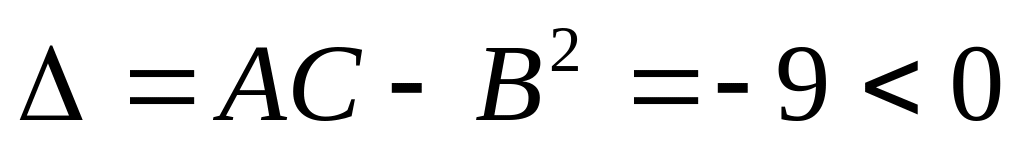Так как
,
то в этой точке нет экстремума.В точке имеем:
,
,
.
В этом случае
.
Так как
и
,
то в этой точке функция имеет минимум
.
ЧТО ДОЛЖЕН ЗНАТЬ СТУДЕНТ
1. Понятие функции нескольких переменных.
2. Область определения и множество значений функции нескольких переменных.
3. Понятие линии уровня.
4. Частные производные функции нескольких переменных.
5. Частные производные высших порядков функции нескольких переменных.
6. Экономический смысл частных производных на примере функции Кобба-Дугласа.
7. Понятие дифференциала функции нескольких переменных.
8. Экстремум функции нескольких переменных.
Контрольный тест
Какая из приведенных функций, является функцией зависящей от двух переменных:
a)
;
б)
;
в)
;г)
.
2.
Для функции
частная производная по переменной
равна:
a)
;
б)
;
в)
;
г)
.
Для функции
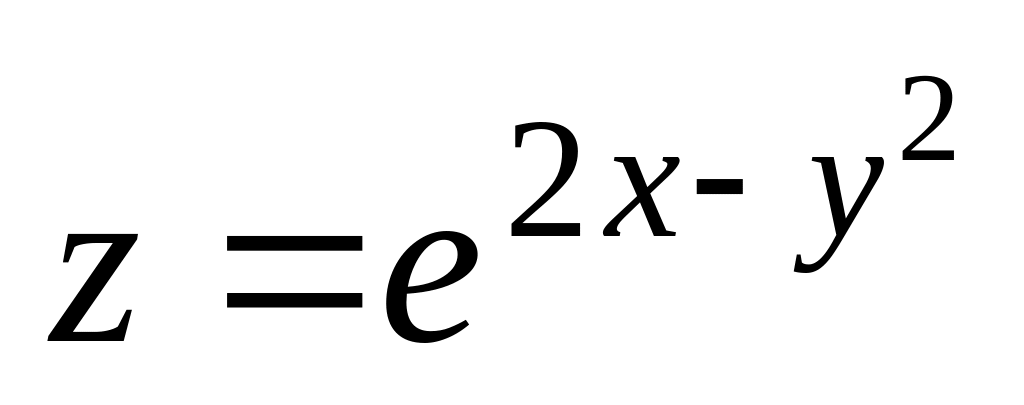частная производная по переменной у
равна:
a)
;
б)
;
в)
;
г)
.
4.
Значение частной
производной
функции
по
переменной х
в точке
равно:
a) -5; б) 10; в) 11; г) 4.
5.
Полный
дифференциал функции
равен:
a)
;
б)
;
в)
;
г)
.
6. Если , , , определены в некоторой окрестности точки и непрерывны в этой точке, то верно:
а)
;
б)
;
в)
;
г)
.
7.Для
функции
равна:
a)
;
б)
;
в)
;
г)
.
8.
Для функции
равна:
а)
;
б)
;
в)
;
г)
.
9.
Исследовать
на экстремум функцию
:
a) функция имеет минимум; б) функция имеет максимум;
в) функция не имеет точек экстремума.
10.
Стационарной
точкой функции
является точка:
а)
;
б)
;
в)
;
г)
.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задача 8.1. Найти частные производные функции:
;
;
;
.
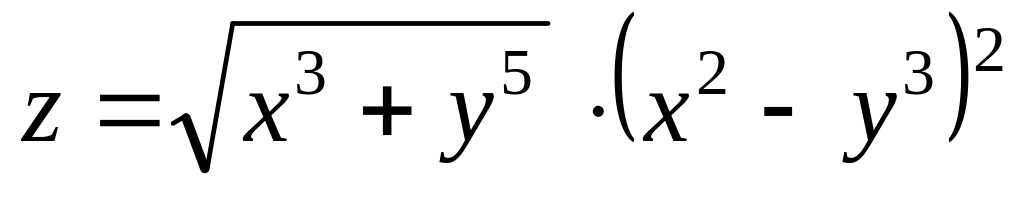Задача 8.2. Найти полный дифференциал функции:
;
.
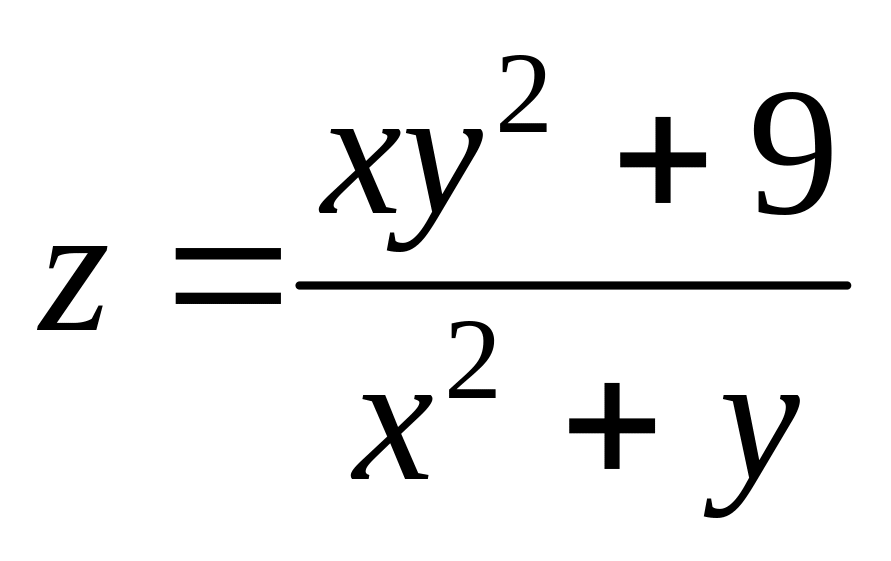Задача 8.3. Найти экстремумы функций:
а)
;
б)
.