10. Численное решение задачи Коши. Метод Эйлера, усовершенствованный метод Эйлера, методы Рунге-Кутты второго и четвертого порядка точности.

Численное решение задачи Коши. Пусть задано диф уравнение первого порядка dy/dx=f(x,y), решением будет множество кривых, если задано начально условие (какая-то точка y(a)=y0), выбирается кривая, удовлетворяющая ему, это и есть решение задачи Коши. Если при решении получается неберущийся интеграл или функция задана не аналитически, можно использовать численные методы интегрирования.

Для численного решения берем за x0 заданную нам точку, некоторый шаг разбиения h, и остальные точки задаются как xj=x0+j*h. Для того, чтобы найти следующее значение y, производятся некоторые преобразования с общим видом диф уравнения, и получается, что y_j+1=y_j+ интеграл от неизвестной зависимости y(x). Проинтегрировать точно не получится, но можно сделать это приближенно.

Метод Эйлера. Метод численного решения задачи Коши, он основан на методе интегрирования левых прямоугольников (площадь под кривой заменяем на площади прямоугольника, взятые по левой стороне). По сути, мы должны получить точки на кривой, но т.к. решаем приближенно, такого не получится из-за погрешностей. В формуле для получения следующего значения y (используется значение функции в левой крайней точке отрезка), получается, что f(x,y)-это производная в точке x0,y0, а производная- это тангенс угла наклона касательной, где dx является шагом разбиения, то есть h. Вместо попадания в нужную точку, мы спустимся на значение дельта1. К значению y0 прибавим dy приближенно найденную, относительно нужной точки вдоль касательной мы сдвинемся вниз. Дальше уже в точке x1 строится касательная и так далее. На первой итерации будет погрешность дельта1, на втором шаге она увеличится и будет дельта1+ дельта2 и тд. Каждый раз погрешность складывается из погрешности, вызванной сдвигом вдоль касательной на предыдущем шаге и погрешности, связанной с неправильным нахождением угла наклона касательной. Имеет порядок, как и у используемого метода интегрирования, т.е. 1.

Усовершенствованный метод Эйлера. Основан на методе интегрирования средних прямоугольников (площадь под кривой заменяем на площади прямоугольника, взятые по середине частичного отрезка). В формуле для получения следующего значения y, используется значение функции в середине отрезка, в седине отрезка точка x_j+1/2 строится касательная к функции, линия, параллельная этой касательной проводится из точки xj,yj. В этом случае погрешность будет значительно меньше, чем в методе Эйлера, но нам придется находить приближенное значение в середине отрезка, для этого можно использовать метод Эйлера. Имеет порядок, как и у используемого метода интегрирования, т.е. 2.

Методы Рунге-Кутты второго и четвертого порядка точности. Основаны на методах интегрирования трапеций и парабол соответственно. Для метода второго порядка, вместо интегрирования мы находим приближенную площадь трапеции. Приближенное промежуточное значение находится методом Эйлера. Для метода 4 порядка находим площадь под параболой: нам нужно 3 точки и значения в них.

11. Численное решение задач урматфиза (краевая задача для линейного ОДУ второго порядка, смешанная задача для уравнения теплопроводности, смешанная задача для волнового уравнения, задача Дирихле для уравнения Лапласа).

Численное решение задач урматфиза.

Краевая задача для линейного ОДУ второго порядка. Задан отрезок, требуется найти решение диф уравнения 2 порядка с переменными коэффициентами, а также заданы краевые условия. Задан f(x), надо найти y(x).

Общий вид ур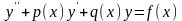

Краевые условия , ,

, .

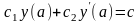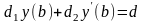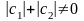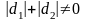Метод редукции к задаче Коши (метод стрельб). Вводятся такие условные обозначения, что вторые производные пропадают. Сводим уравнение 2 порядка к системе двух уравнений 1 порядка, то есть к задаче Коши.

Метод конечных разностей. Задается сетка с шагом h, где иксы задаются x0+h*I, решением уравнения являются значения игриков в этих точках. В уравнении общего вида производные заменяем на конечноразностные производные и на концах отрезка заменяем односторонними производными. Получается система из 2 уравнений, если записать ее в матричном виде, получится матрица с 3 диагоналями, решить эту систему можно методом прогонки.

Смешанная задача для уравнения теплопроводности. Задан стержень из теплопроводящего материала, температура на концах стержня, а его поверхность теплоизолирована. При нагревании в разных точках стержня в разное время температура будет меняться согласно уравнению теплопроводности (вторая производная температуры по иксу, равна первой производной температуры по времени). Еще нам заданы начальные условия: температура в начальный момент времени в любой точке стрежня и краевые условия (как температура меняется на краях в зависимости от времени).

Строится сетка по времени и по пространству икс (от 0 до 1), для икса шаг – h, для t- шаг тау. Из начальным и краевых условий, нам известны значения иксов в узловых точках и значения на концах (т.е. в точке 0 и 1) по оси игрик во всех узловых точках. Задача решается методом конечных разностей. Заменяем производные на разностные, проводим замены и алгебраические преобразования, выйдет система линейных уравнений, которую решают методом прогонки и таким образом получим значения иксов, получим значение j-того временного слоя, и дальше увеличивая j на единицу и все повторяется для нахождения остальных слоев. Существуют явная схема, при которой про 3 известным значениям временных слоев (полоски t=1,t=2 и тд) находим 1 неизвестное и неявная схема, по одному известному три неизвестных, при том неявная смеха всегда устойчива (от шага к шагу ошибка не возрастает), а явная устойчива только при лямбда<1/2.

Смешанная задача для волнового уравнения. Есть струна, закрепленная в точках 0 и 1, ее оттягивают или ударяют по ней, и вот эти колебания удовлетворяют волновому уравнению теплопроводности (вторая производная колебаний по иксу, равна второй производной колебаний по времени), x-это какая-то точка на струне, t-время. Заданы начальные и краевые условия. Для решения используется метод конечных разностей: в исходное уравнение и условия вместо производных подставляются их конечноразностные аналоги, вводится число Курента (заменяем отношение лямбда на тау).

Задача Дирихле для уравнения Лапласа методом сеток. Задана прямоугольная область Омега и уравнение Лапласа (элиптического вида), граниченые условия и нужно найти на сетке зависимость в любой точке Y от X. Для решения используется метод конечных разностей: в исходное уравнение вместо производных подставляются их конечноразностные аналоги. На этой сетке находим искомую функцию для всех внутренних узлов