5.Аппроксимация. Постановка задачи. Приближение по методу наименьших квадратов.

Аппроксимация. Постановка задачи. При решении задачи аппроксимации задаются значения функции в разных точках в виде таблицы и считается, что значения функции содержат значительную долю случайной погрешности. Наша задача- найти функцию, которая проходила бы между точками наилучшим образом.

Необходимо определить критерий качества аппроксимации, для этого строим функцию штрафа, где штраф-это отклонение функции в заданной точке x от ее значения по y. Считаем, что штрафы независимы и тогда функция штрафа равна сумме отдельных нарушений. Далее надо найти функцию, определяющую как штраф зависит от нарушения, чтоб выбрать вид функции надо рассмотреть 2 условия: задача должна быть простой и иметь разумное решение.

Приближение по методу наименьших квадратов. Общий штраф будет суммой квадратов отклонений, где отклонение это разность значения многочлена в данной точке и значение игрика, таким образом получалось, что общий штраф зависит только от коэффициентов многочлена. Необходимо минимизировать данную функцию, для этого ищутся производные по каждой переменной и приравниваются к нулю, и после решения получившийся системы уравнений мы найдем все коэффициенты ai. Таким образом мы найдем такую кривую, для которой сумма квадратов отклонений всех точек от нее минимальна.

6.Постановка задачи численного дифференцирования. Правая, левая, центральная разностные производные (первая и вторая). Их теоретические оценки с помощью разложения по формуле Тейлора. Понятие порядка точности формулы. Порядок точности различных методов численного дифференцирования. Общая практическая оценка погрешности метода, исходных данных и округления разностных производных.

Постановка задачи численного дифференцирования. В тех случаях, когда функцию сложно продифферинцировать или результат будет получен неточный используют численное дифференцирование (например, когда функция задана дискретно).

Правая, левая, центральная разностные производные (первая и вторая).

Вместо точного значения производной, то есть предельного отношения мы берем конечную разность функций.

Значение производной функции в некоторой точке - это предел отношения приращения функции к приращению аргумента, где аргумент стремится у нулю. Приращение взято в одну сторону, в обратную и по середине.

Т.к. вычисление пределом задача бесконечно затратная, мы их отбрасываем и записывает приближенные равенства.

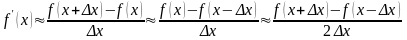
Если переписать это в немного другом виде: заменить deltaX на h (т.е расстояние между 2 точками), а f(x) записывать как fj, то получится выражение, где первое – это право разностная производная, второе – лево разностная, третье- центрально разностная.

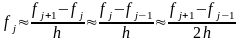
Значение для второй производной ищется по формуле

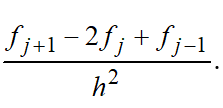
Теоретические оценки разностных производных с помощью разложения по формуле Тейлора. Например, для оценки право разностной производной, раскладываем функцию f(x) по формуле Тейлора до второго слагаемого (т.к. ряд убывающий и в принципе зная оценку второго слагаемого, можно оценить первое) ,

заменяем x на x_j+1. Затем проводим некие алгебраические преобразования, и получается, что в левой части равенства оказывается сама право разностная производная, а в правой части остаются точное значение производной и плюс остаточный член, т.е. погрешность. На основании этой формулы можем сказать, что погрешность будет не больше h/2 умноженное на максимальное значение второй производной.

Понятие порядка точности формулы. При оценке разностных производных с помощью разложения по формуле Тейлора получаются неравенства, где слева модуль разности между приблизительным и точным значением, а справа шаг разбиения в какой-то степени, умноженный на максимум какой-то производной. И вот степень при h является порядком точности формулы/метода.

Порядок точности различных методов численного дифференцирования.

правая и левая разностные производные имеют первый порядок точности, центральные разностные производные (первая и вторая) – второй порядок.

Общая практическая оценка погрешности метода, исходных данных и округления разностных производных. При использовании компьютера, мы ограничены разрядом мантиссы. В конечно-разностных формулах вместо точных значений функции f_j используются приближенные f_j+_{j .} Выводится формула, по которой можно оценить общую погрешность, но оказывается, что при сильном уменьшении h, в какой-то момент погрешность начинает, наоборот расти, что связано с погрешностью округления. Чтобы найти это значение h, после которого уже будет идти увеличение погрешности, есть формула, из которой следует, что шаг не должен быть меньше, чем 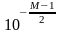(М-количество десятичных разрядов мантиссы). При численном дифференцировании теряется половина знаков после запятой.

7.Численное интегрирование функций. Интерполяционные квадратурные формулы прямоугольников, трапеций и парабол. Порядок точности методов численного интегрирования. Общая практическая оценка погрешности метода, исходных данных и округления.

Численное интегрирование функций. Существует много сложных и неберущихся интегралов, для того чтобы проинтегрировать функцию используют численное интегрирование, т.е. нахождение приблизительного значения. Суть состоит в том, что разбиваем площадь под кривой на площадь каких-то фигур, и интеграл считается как сумма этих частичных интегралов. Есть 5 основных методов численного интегрирования.

Интерполяционные квадратурные формулы прямоугольников, трапеций и парабол. При методе прямоугольников вместо площади криволинейной фигуры вычисляются площади прямоугольников, для левых прямоугольников берется площадь прямоугольника по левой границе, для правого по правой и для серединных – значение функции в середине отрезка. По сути, это интерполяция многочлена нулевой степени.

Левых

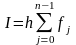
правых

серединных

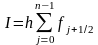
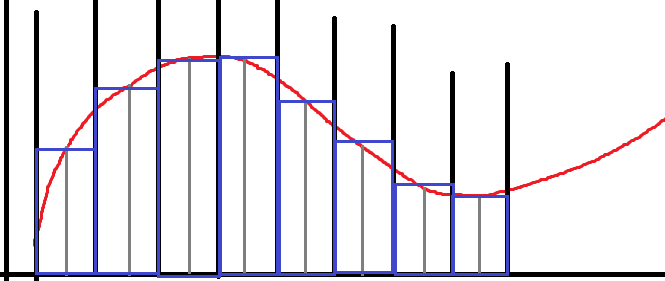
Метод трапеций, находятся площадь трапеций, тут уже интерполяционный многочлен первой степени

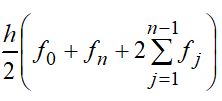
Метод парабол. Ищется площадь под параболой. Сама парабола строится через 3 точки, то есть 2 узловые и их середина

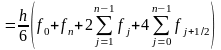
Порядок точности методов численного интегрирования. Прямоугольников левых и правых -1, серединных и трапеций-2, парабол-4.

Общая практическая оценка погрешности метода, исходных данных и округления. Для оценки погрешностей (аналогично разностным производным) раскладываем функцию по Тейлору, проводим замены, в итоге получаем формулу, в которой есть точное и приближенное значение интеграла по какому-то методу. Но оценить саму погрешность мы не можем, т.к. там вылезают производные, значения которых нам не известны, но зато мы можем узнать порядок точности формул, то есть степень h.

Общая погрешность будет зависеть от разрядности мантиссы. Там как в численном дифференцирование выводится оптимальное значение шага h, при котором погрешность минимальна. И так же половина десятичных разрядов пропадает.