6. Переходный процесс при действии постоянного возмущающего момента.

Рис. 5. Структурная схема замкнутой гиросистемы как объекта управления.

При помощи пакета Matlab 6.5 построим переходный процесс (реакция системы на единичную ступеньку на входе)

Рис. 6. Переходный процесс замкнутой гиросистемы как объекта управления.

7. АЧХ замкнутой гиросистемы.

Рис. 7. АЧХ замкнутой гиросистемы.

8. Структурная схема гиросистемы с сопутствующей нелинейностью. Передаточная функция приведенной линейной части.

Рис. 8. Структурная схема гиросистемы.

Разделим систему на приведенную линейную и нелинейную части. В этом случае система будет иметь следующий общий вид:

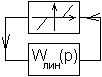
где

9. Обоснование возможности применения метода гармонической линеаризации. ЛАЧХ приведенной линейной части.

Построим ЛЧХ для приведенной линейной части (см. сл. стр.) Как видно из ЛЧХ, линейная часть системы обладает свойствами фильтра, следовательно, выполняется гипотеза фильтра, необходимая для применения метода гармонической реализации.

Рис. 9. ЛАЧХ приведенной линейной части.

10. Гармоническая линеаризация нелинейной системы. Условие амплитудно-фазового баланса.

Рассмотрим нелинейный элемент. При подаче на вход нелинейного элемента гармонического сигнала получим на его выходе сигнал следующего вида:

Рис. 10. Преобразование сигнала нелинейным элементом.

где .

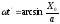Таким образом, нелинейность из входной гармоники (амплитуды большей, чем Х₀) создает спектр гармоник (согласно теории Фурье) с амплитудами, не зависящими от амплитуды входного сигнала.

Поскольку ЛАЧХ линейной части обладает свойствами фильтра, следовательно она будет фильтровать все гармоники, кроме 1 (поскольку частоты остальных гармоник располагаются в области ЛАЧХ с сильным ослаблением). Таким образом, на вход нелинейного элемента поступит только первая гармоника.

Исходя из вышесказанного, возможно существование автоколебаний в системе.

Произведем гармоническую линеаризацию нелинейного элемента.

Пусть на вход нелинейного элемента поступает сигнал:

Нелинейный элемент представим в виде:

С учетом принятой гипотезы фильтра, разложив в ряд Фурье, получим:

где

где 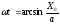. Интегрируем с помощью пакетаMaple 8.0 и получаем:

Для однозначных нелинейностей:

Уравнение амплитудно-фазового баланса:

Построим с помощью пакета Maple 8.0 графическую зависимость :

Рис. 11. Коэффициент гармонической линеаризации q.

Можно также записать:

Таким образом, коэффициент гармонической линеаризации q может принимать значения из диапазона [0;1].

11. Афх приведенной линейной части и инверсная характеристика гармонически линеаризованного элемента.

Инверсная характеристика линеаризованного элемента имеет вид:

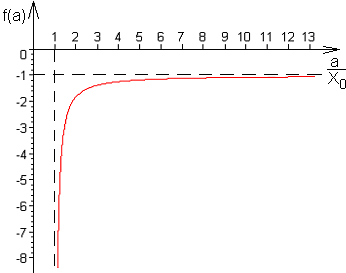
Рис. 12. Инверсная характеристика гармонически линеаризованного элемента.

На АФЧЧ инверсная характеристика, таким образом, превратится в луч идущий из в точку –1.

Рис. 13. АФЧХ линейной части.

Для определения точек пересечения АФЧХ линейной части и инверсной характеристики нелинейного элемента, рассмотрим увеличенный кусочек (на рисунке пунктиром).

Рис. 14. АФЧХ линейной части и инверсная характеристика нелинейного элемента (увеличено).

Видим, что АФЧХ линейной части пересекает действительную ось в точке -0.0856, а инверсная характеристика заканчивается в точке -1, таким образом нет точек пересечения инверсной характеристики и АФЧХ приведенной линейной части, а значит уравнение баланса фаз не может быть выполнено. Это соответствует случаю отсутствия периодических решений, а значит автоколебания на выходе не установятся.