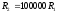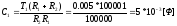3. Оптимизация параметров упруго-диссипативной связи динамических элементов гиросистемы.

На данном этапе предполагаем μ_α = μ_β = 0 (поскольку они малы по сравнению с μ) и будем оптимизировать μ и С.

Тогда (при μ_α = μ_β = 0)

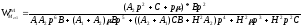
Данная передаточная функция обладает следующим свойством: на АЧХ данной передаточной функции существуют две инвариантные точки (все АЧХ пересекаются в них). Положение этих точек на АЧХ изменяется при изменении С.

Целью задачи оптимизации, решаемой в данном пункте, является минимизация максимумов АЧХ ПФ системы, как объекта стабилизации, а именно минимизация резонансных пиков АЧХ. Оптимизация разбивается на две подзадачи:

1) Поиск значения С^*, при котором инвариантные точки будут располагаться на одном уровне (при таком расположении обеспечивается минимальное значение амплитуды обеих инвариантных точек).

2) Поиск значения μ*, обеспечивающего минимальное значение резонансных пиков.

Приравниваем 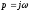, получаем:

W(jω) =

Далее нужно найти такие две инвариантные точки, чтобы выполнялось равенство:

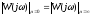
Устремляя μ–>0 а потом μ–>∞ получаем:

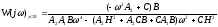
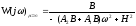
Подставляем числа из условия, раскрываем знак модуля и получаем систему уравнений:

которое решаем относительно ω с помощью пакета Mathcad 2001i. Получаем 8 решений:

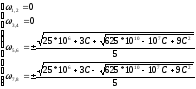
Нулевые и отрицательные корни отбрасываем, и тогда получаем:

Далее находим оптимальное С^*, пользуясь тем, что

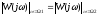приμ = 0

Также подставляем числа из условия, а также значения Ω₁ и Ω₂, раскрывая знак модуля получаем систему уравнений:

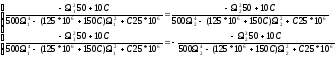
Решаем его относительно С в пакете Mathcad 2001i и получаем (отбрасывая комплексные корни):

С^*≈ 5*10⁵

Подставляем С* в выражения для Ω₁ и Ω₂ и находим их численные значения:

Ω₁ ≈ 303.5 Гц

Ω₂ ≈ 491.1 Гц

Далее, на основе найденного С* оптимизируем μ (находим μ^*), для чего вначале нужно найти μ₁^*, μ₂^*, при которых в каждой из инвариантных точек будет экстремум АЧХ (это обеспечивает минимум “всплеска” АЧХ в соответствующих инвариантных точках) а для этого, в свою очередь, нужно решить систему уравнений:

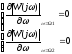
Здесь в качестве ПФ W(jω) используем передаточную функцию стабилизации:

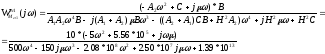
Здесь из первого уравнения находим μ₁^*, из второго – μ₂^*, получаем следующие решения (отбрасывая комплексные корни):

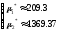
Находим μ^*:

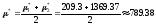
4. Ачх механической части гиросистемы с оптимальными параметрами μ* и с*.

ПФ механической части системы, как объекта стабилизации (берем из предыдущего пункта:

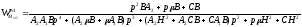
Строим АЧХ механической части гиросистемы для трех случаев (на одном графике): 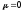,и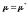

Для :

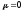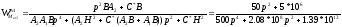
Для :

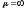Для :

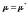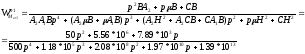
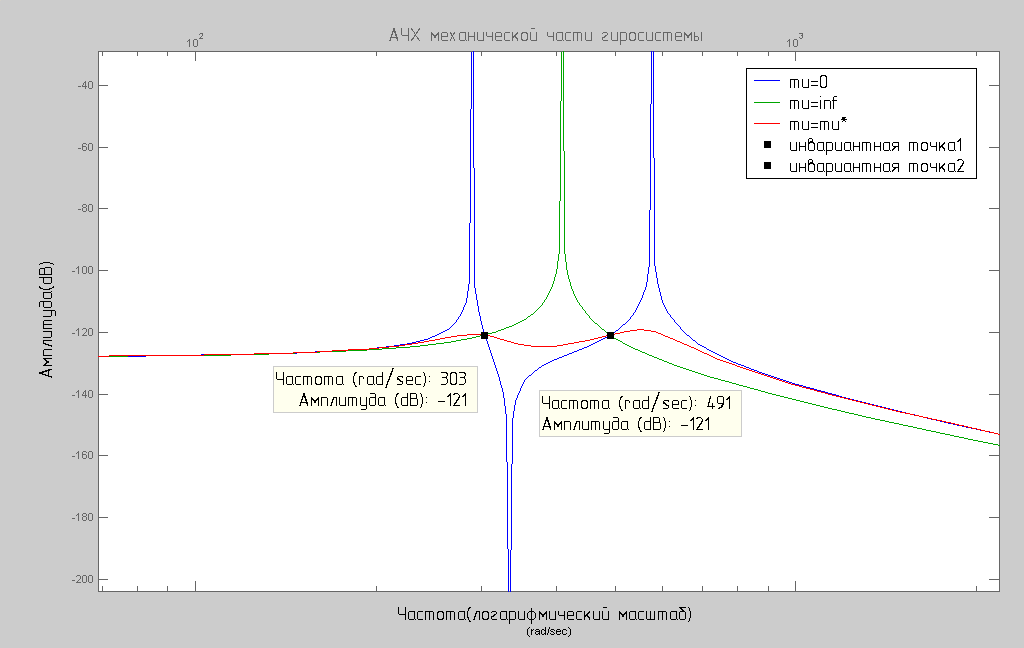
Рис. 2. АЧХ механической части гиросистемы.

Для каждой из трех АЧХ С = С^*.

5. Синтез цепи обратной связи. Лчх разомкнутой цепи.

Определим требуемый статический коэффициент усиления в цепи обратной связи:

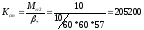
Далее построим ЛЧХ разомкнутой цепи (это нужно, поскольку в соответствии с критерием Найквиста-Михайлова мы судим об устойчивости замкнутой системы по устойчивости разомкнутой системы).

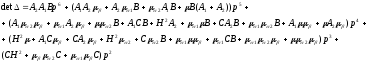– передаточная функция гиросистемы как объекта управления, здесьПодставляя численные значения коэффициентов А₁, А₂, B, H, C = C^*, μ = μ^*, μ_α1, μ_α2 и μ_β, получаем передаточную функцию разомкнутой гиросистемы (знак “–”выносится впоследствии за обратную связь, поэтому здесь мы его не учитываем) :

Строим ЛЧХ для данной передаточной функции.

Рис. 3. ЛАЧХ разомкнутой системы.

Видим, что замкнутая система неустойчива, то есть необходимо использовать корректирующий контур. Используем корректирующий контур в цепи обратной связи (К(р)) для достижения статической устойчивости и требуемого качества.

Система, как уже указано, неустойчива. Для ее стабилизации необходимо скорректировать форму ЛЧХ на средних частотах таким образом, чтобы амплитуда, при которой фазовая характеристика пересекает уровень -180⁰ была меньше 0Дб, и в то же время фаза, при которой амплитудная характеристика пересекает уровень 0Дб была больше -180⁰ (см. критерий устойчивости Найквиста-Михайлова).

Это можно достигнуть применением интегрирующего корректирующего устройства с передаточной функцией вида:

где .

Выберем следующие параметры корректирующего фильтра:

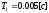
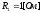
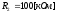
Построим ЛЧХ скорректированной системы, на одном графике с ней для сравнения также построим ЛЧХ нескорректированной системы, а также ЛЧХ корректирующего контура.

Видим, что с добавлением корректирующего контура система стала устойчивой со следующими параметрами запасов устойчивости:

1) По амплитуде: По амплитуде = 26.6дБ;

2) По фазе = 91.4⁰.

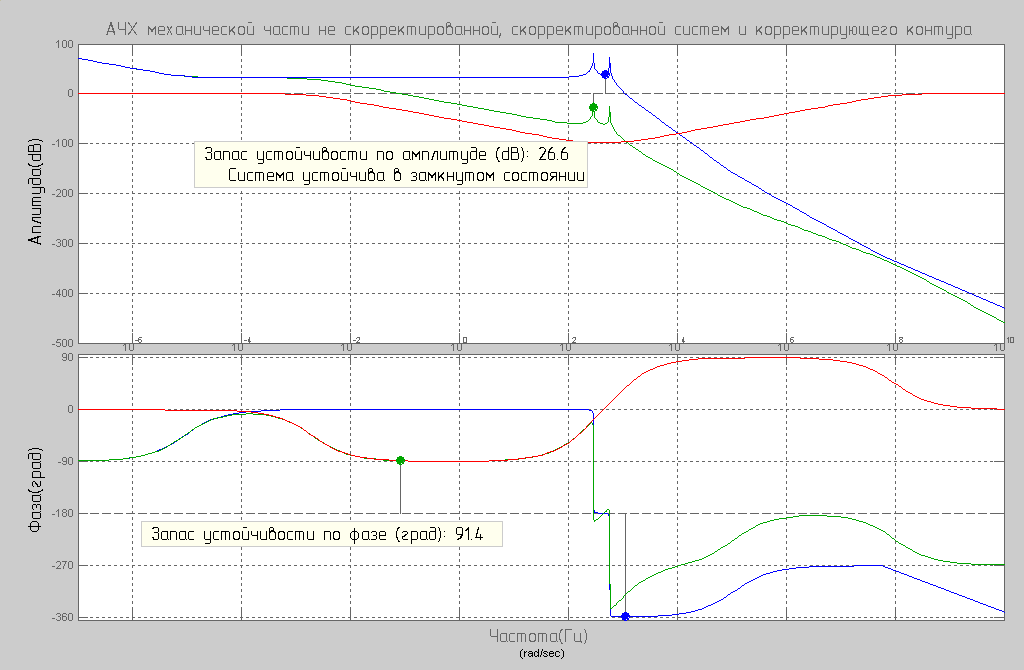
Рис. 4. ЛАЧХ не скорректированной разомкнутой системы (синий цвет); скорректированной разомкнутой системы (зеленый цвет) и корректирующего контура (красный цвет).

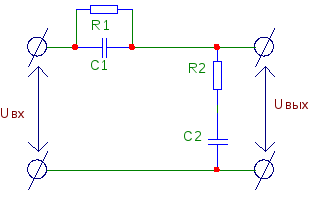
Приведем электрическую схему данного устройства:

Здесь

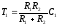
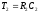
Решая данную систему относительно R₂ и С₂ получаем: