
ЭКЗАМЕН
.docx|
Первообразная Определение.
Первообразной для функции
Теорема: Если
функция
|
Определение неопределенного интеграла и его свойства. Определение:
Неопределенным интегралом для
функции
Обозначается:
Свойства неопределенного интеграла:
|
|
Интегрирование по частям. Интегрирование по частям есть действие обратное дифференцированию произведения. Имеем:
Проинтегрируем обе части равенства:
Замечание: Если под знаком
интеграла имеем дробь
|
Интегрирование заменой переменной.
Рассмотрим формулу:
В данном интеграле сделана замена
|
|
Интегрирование рациональных дробей. Разложение правильной дроби на простейшие. Определение: Рациональной дробью называется отношение двух многочленов.
Определение:
Рациональная дробь
К простейшим рациональным дробям относятся дроби: 1)
2)
3)
4)
|
|
Интегрирование простейших рациональных дробей.
|
|
Интеграл:
подстановки
от рациональной функции:
В результате получаем:
|
|
Вычисление
интегралов вида:
Пусть
В данном интеграле сделаем замену
Далее имеем:
Сделав подстановку, получим:
Таким образом, вычисление данного интеграла с помощью указанной замены сводится к вычислению интеграла от рациональной функции.
|
|
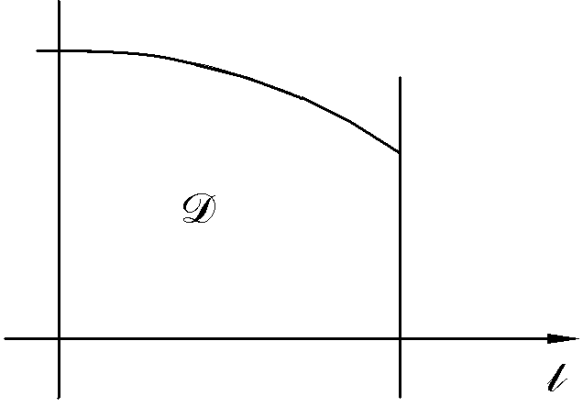
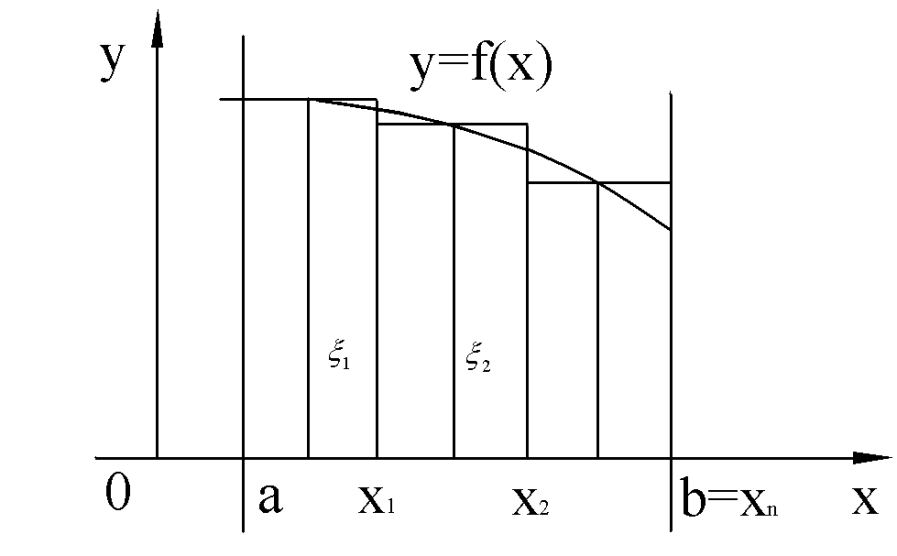
Задачи, приводящие к понятию определенного интеграла. Задача 1. Вычислить площадь криволинейной трапеции. Во-первых, мы должны дать определение криволинейной трапеции. Во-вторых, должны дать определение площади криволинейной трапеции. В-третьих, должны указать способ вычисления площади криволинейной трапеции. Определение. Криволинейной трапецией называется фигура, ограниченная прямой l, двумя прямыми, перпендикулярными прямой l и непрерывной кривой, которая расположена по одну сторону от прямой l и любой прямой, перпендикулярной l, пересекается не более чем в одной точке.
Если прямую
l взять за ось OX;
OY
|
|
Определение. Криволинейной
трапецией называется фигура, ограниченная
осью OX, прямыми
x=a; x=b и графиком
непрерывной функции
Далее, определение площади криволинейной трапеции и способ вычисления этой площади дадим одновременно. При решении этих задач мы будем пользоваться следующими известными фактами:
Задача 2.
Найти массу неоднородного стержня
При решении этой задачи мы будем пользоваться следующими известными фактами:
|
|
Определение определенного интеграла. Пусть
Отрезок
Это разбиение
обозначим через (T),
В каждом из
участков разбиения произвольным
способом выберем по точке
Составим
сумму
Заметим, что
интегральная сумма зависит как от
разбиения (T), так и от
выбора точек
Определение. Конечный
предел интегральных сумм при
Определенный
интеграл обозначается следующим
образом:
Определение определенного интеграла можно записать в следующем виде:
если последний предел существует. Геометрический смысл определенного интеграла. Если
подынтегральная функция
Механический смысл определенного интеграла. Если
подынтегральная функция непрерывна
и неотрицательна на
|
|
Теорема существования определенного интеграла.
Если
Свойства определенного интеграла. 1)
2)
3) Постоянный множитель можно выносить за знак интеграла.
4)
5)
6)
7) Если
8) Если
|
|
Интеграл с переменным верхним пределом.
Пусть
Далее
покажем, что функция
Теорема. Если
Доказательство. По определению
производной
где с
расположено между
Последнее
равенство имеет место в силу теоремы
о среднем. Подставляя вместо
Точка с расположена между
|
|
Формула Ньютона-Лейбница.
Теорема. Справедлива
формула
Доказательство. Рассмотрим интеграл с
переменным верхним пределом
|
|
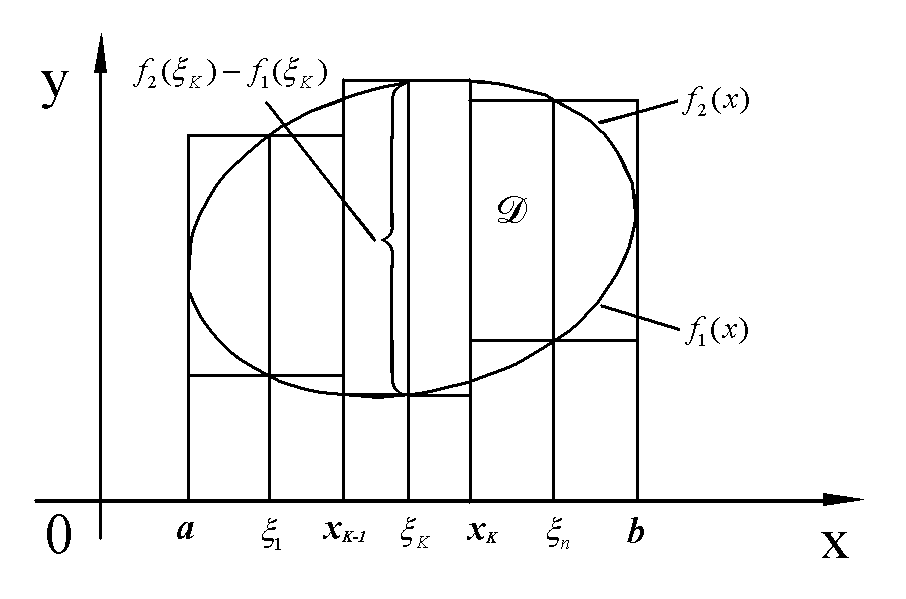
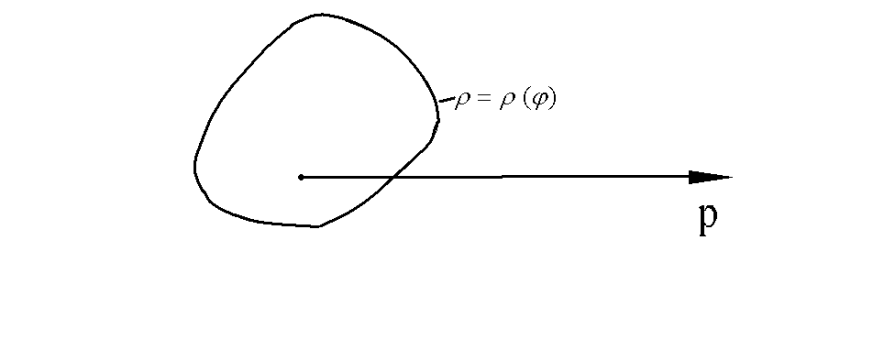
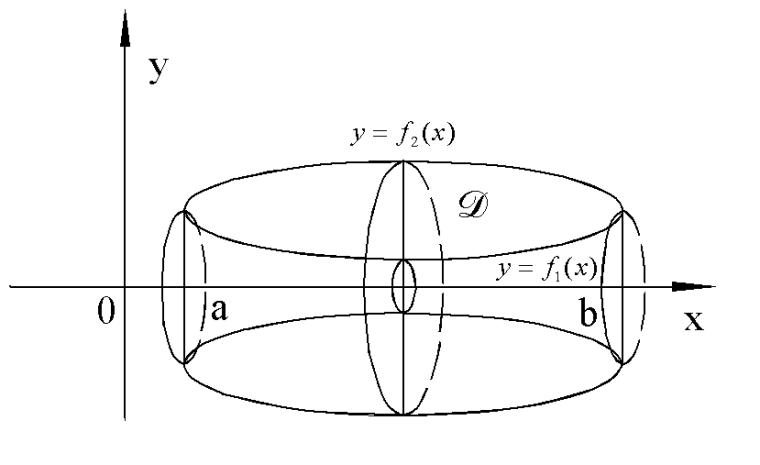
Вычисление площади фигуры в декартовой системе координат.
Определение. Площадью
S области D
называется
В определении площади области D
сумма, стоящая под знаком предела
является интегральной суммой для
функции
Если
|
|
Вычисление площади фигуры в полярной системе координат.
Два частных случая.
|
|
Вычисление длины кривой.
Вычисление объемов тел по площадям параллельных сечений.
Вычисление объемов тел вращения. Пусть тело является телом вращения криволинейной трапеции вокруг оси OX.
В этом случае
Пусть теперь тело является телом вращения фигуры D, которая не пересекает оси OX, причем любая прямая, параллельная оси OY пересекает границу D не более чем в двух точках.
|
|
Несобственные
интегралы от функций, заданных на
конечном отрезке
Пусть функция
Рассмотрим
произвольное
Интеграл
Несобственный
интеграл
Если
Пусть теперь
Несобственный
интеграл
Далее
рассмотрим случай, когда
Несобственный
интеграл
|
|
Несобственные интегралы от непрерывных функций по бесконечному промежутку. Пусть
Рассмотрим
интеграл Положим по определению
Интеграл
Пусть теперь
функция
Несобственный
интеграл
Далее, пусть
функция
Несобственный
интеграл
при условии, что оба интеграла справа сходятся. Заметим, что
вместо 0 можно взять любое конечное
число а и при этом сходимость
несобственного интеграла
|
|
Интегрирование по частям в определенном интеграле. Теорема.
Справедлива формула
Доказательство.
Имеем:
Почленно проинтегрируем последнее равенство
Замена переменной в определенном интеграле.
Пусть
Справедлива формула
Доказательство.
Так как
Функция
В самом деле,
применяя правило дифференцирования
сложной функции, получим:
Используя формулу
Ньютона-Лейбница, получим:
|
|
Дифференциальные уравнения 1го порядка. В общем виде
дифференциальное уравнение первого
порядка записывается следующим
образом:
В частных
случаях в левую часть уравнения в
явном виде могут не входить
Если уравнение
(1) можно разрешить относительно
Задача Коши. Теорема Коши о существовании и единственности решения задачи Коши. Задача Коши:
Найти решение дифуравнения
Теорема
Коши: Если функция
Определение: Любое решение задачи Коши называется четным решением дифуравнения. Определение: Совокупность всех частных решений дифуравнения называется общим решением этого уравнения. Графиком частного решения на плоскости является кривая, которая называется интегральной кривой.
|
|
Дифуравнение с разделяющимися переменными. Определение:
Уравнение вида: Для решения дифуравнения с разделяющимися переменными надо разделить переменные и проинтегрировать. Однородные дифуравнения первого порядка. Определение:
Дифференциальное уравнение вида
Это уравнение с помощью
замены
|
|
Линейные дифференциальные уравнения первого порядка. Определение:
Дифференциальное уравнение вида:
называется линейным уравнением. Решение
линейного уравнения можно искать в
виде:
Уравнения Бернулли Определение : Уравнение вида
называется уравнением
Бернулли. Если
|

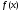 в интервале
в интервале
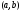 называется функция
называется функция
 ,
производная которой равна
,
производная которой равна
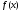 ,
т.е.
,
т.е.
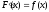 .
.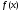 в интервале имеет первообразную
в интервале имеет первообразную
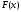 ,
то любая другая первообразная отличается
от данной на константу.
,
то любая другая первообразная отличается
от данной на константу. называют совокупность всех ее
первообразных
называют совокупность всех ее
первообразных
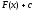 .
. .
.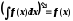
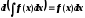
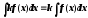
 .
.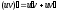
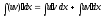
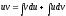 отсюда получаем:
отсюда получаем: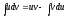
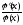 ,
числитель которой есть производная
знаменателя, то интеграл от этой дроби
равен логарифму натуральному от модуля
знаменателя!!!
,
числитель которой есть производная
знаменателя, то интеграл от этой дроби
равен логарифму натуральному от модуля
знаменателя!!!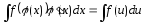 ,
где
,
где
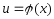 в
следующем виде:
в
следующем виде: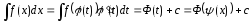 ,
где
,
где
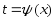 обратная функция для функции
обратная функция для функции
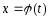 .
Обратим внимание на то, что при замене
переменной
.
Обратим внимание на то, что при замене
переменной
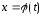 последняя функция должна иметь
обратную.
последняя функция должна иметь
обратную.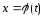 .
Сложность заключается в том, что таких
замен бесконечно много и нужно подобрать
такую, чтобы вновь полученный интеграл
был проще исходного.
.
Сложность заключается в том, что таких
замен бесконечно много и нужно подобрать
такую, чтобы вновь полученный интеграл
был проще исходного.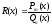 ,
где
,
где
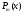 и
и
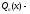 многочлены соответственно степеней
m и n.
многочлены соответственно степеней
m и n.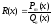 называется правильной, если степень
числителя меньше степени знаменателя,
т.е.
называется правильной, если степень
числителя меньше степени знаменателя,
т.е.
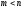 ,
в противном случае рациональная дробь
– неправильная.
,
в противном случае рациональная дробь
– неправильная.

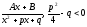
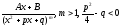
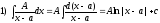
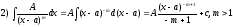
 с помощью
с помощью
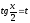 всегда сводится к интегралу
всегда сводится к интегралу
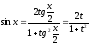
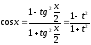
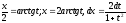
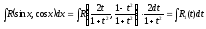
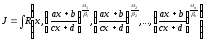 dx,
где
dx,
где
 ,
,
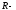 символ рациональности функции.
символ рациональности функции. натуральные
числа.
натуральные
числа.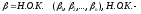 наименьшее общее кратное.
наименьшее общее кратное.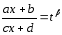 ,
тогда
,
тогда
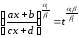 ,
где
,
где
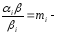 целое положительное число для любого
целое положительное число для любого
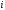 ,
,
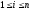 .
.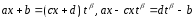
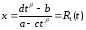 и
и
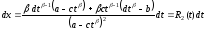

 OX,
тогда определение криволинейной
трапеции можно дать следующим образом.
OX,
тогда определение криволинейной
трапеции можно дать следующим образом. ,
,
 .
.
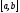 с плотностью
с плотностью
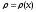 .
.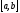 постоянна
и равна
постоянна
и равна
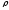 ,
то масса отрезка
,
то масса отрезка
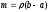 .
.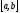 разбить на конечное число частей, то
масса отрезка равна сумме масс его
частей.
разбить на конечное число частей, то
масса отрезка равна сумме масс его
частей.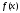 – произвольная функция, заданная на
отрезке
– произвольная функция, заданная на
отрезке
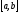 .
.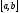 произвольным способом разобьем на n
частей точками:
произвольным способом разобьем на n
частей точками:
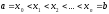 .
.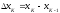 .
.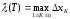 .
.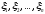 ,
,
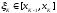 .
.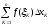 ,
которая называется интегральной
суммой.
,
которая называется интегральной
суммой.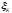 .
.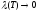 называется
определенным интегралом от функции
называется
определенным интегралом от функции
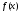 на отрезке [a,b].
на отрезке [a,b].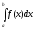 .
.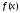 называется подынтегральной функцией,
называется подынтегральной функцией,
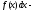 подынтегральным
выражением,
подынтегральным
выражением,
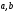 – пределы интегрирования, а – нижний,
b – верхний предел
интегрирования.
– пределы интегрирования, а – нижний,
b – верхний предел
интегрирования.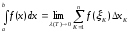 ,
,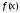 непрерывна и неотрицательна на
отрезке
непрерывна и неотрицательна на
отрезке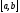 ,
то
,
то
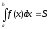 есть площадь соответствующей
криволинейной трапеции.
есть площадь соответствующей
криволинейной трапеции. ,
то
,
то
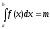 есть масса неоднородного стержня
есть масса неоднородного стержня
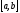 с плотностью
с плотностью
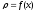 .
.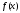 непрерывна на отрезке
непрерывна на отрезке
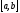 ,
то
,
то
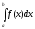 существует.
существует.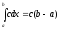

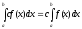 ,
с=const.
,
с=const.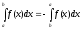
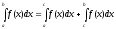

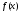 знакопостоянна на
знакопостоянна на
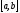 ,
то
,
то
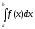 имеет
тот же знак, что и
имеет
тот же знак, что и
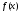 .
. ,
,
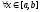 ,
то
,
то
 .
.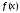 непрерывная функция на отрезке
непрерывная функция на отрезке
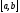 .
Рассмотрим интеграл
.
Рассмотрим интеграл
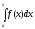 ,
где верхний предел
,
где верхний предел
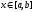 .
Верхний предел x и x
под знаком интеграла разные и имеют
разный смысл. Верхний предел x
является произвольной фиксированной
точкой отрезка
.
Верхний предел x и x
под знаком интеграла разные и имеют
разный смысл. Верхний предел x
является произвольной фиксированной
точкой отрезка
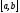 ,
а x под знаком интеграла
является переменной, которая изменяется
от a до верхнего предела
x. Интеграл
,
а x под знаком интеграла
является переменной, которая изменяется
от a до верхнего предела
x. Интеграл
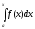 называется интегралом с переменным
верхним пределом, т.к. верхний предел
x может принимать любое
значение из отрезка
называется интегралом с переменным
верхним пределом, т.к. верхний предел
x может принимать любое
значение из отрезка
 .
По условию
.
По условию
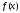 непрерывна на любом отрезке
непрерывна на любом отрезке
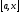 ,
,
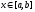 ,
то по теореме существования интеграл
,
то по теореме существования интеграл
 существует для любого
существует для любого
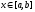 ,
поэтому
,
поэтому
 является функцией от x.
является функцией от x.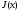 является
дифференцируемой функцией.
является
дифференцируемой функцией.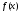 непрерывна на отрезке
непрерывна на отрезке
 ,
то производная от интеграла с переменным
верхним пределом равна подынтегральной
функции, т.е.
,
то производная от интеграла с переменным
верхним пределом равна подынтегральной
функции, т.е.
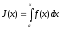 является первообразной для
подынтегральной функции на
является первообразной для
подынтегральной функции на
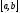 ,
,
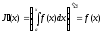
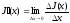
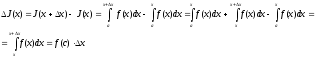
 и
и
 .
.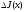 полученное выражение, будем иметь
полученное выражение, будем иметь .
. и
и
 ,
поэтому
,
поэтому
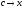 при
при
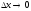 .
Так как
.
Так как
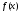 непрерывна в точке x,
то
непрерывна в точке x,
то
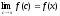 .
.
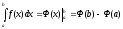 ,
где Ф(x) какая-либо
первообразная для подынтегральной
функции
,
где Ф(x) какая-либо
первообразная для подынтегральной
функции
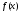 .
.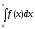 .
Этот интеграл является первообразной
для функции
.
Этот интеграл является первообразной
для функции
 .
Пусть
.
Пусть
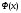 –
произвольная другая первообразная
для
–
произвольная другая первообразная
для
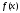 .
Две различные первообразные для
функции
.
Две различные первообразные для
функции
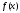 различаются на константу. Поэтому
различаются на константу. Поэтому
 .
Положим верхний предел
.
Положим верхний предел
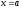 ,
тогда получим:
,
тогда получим:
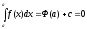 ,
отсюда
,
отсюда
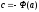 ,
,
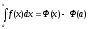 .
В последнем интеграле вместо верхнего
предела x подставим
.
В последнем интеграле вместо верхнего
предела x подставим
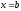 ,
тогда получим:
,
тогда получим:
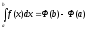 .
.
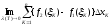 ,
если предел существует. Если данный
предел не существует, то область D
площади не имеет. Если область D
имеет площадь, то она называется
квадрируемой.
,
если предел существует. Если данный
предел не существует, то область D
площади не имеет. Если область D
имеет площадь, то она называется
квадрируемой.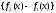 ,
поэтому
,
поэтому
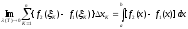 и
и .
.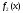 и
и
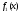 непрерывные функции на отрезке
непрерывные функции на отрезке
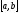 ,
то по теореме существования определенного
интеграла можно утверждать, что
область D
имеет площадь, т.е. область D
квадратируема.
,
то по теореме существования определенного
интеграла можно утверждать, что
область D
имеет площадь, т.е. область D
квадратируема.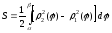
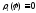 ,
а
,
а
 .
.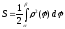
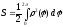
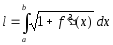


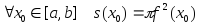 и
и
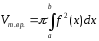 .
.
 .
.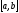 ,
но неограниченных на этом отрезке.
,
но неограниченных на этом отрезке.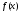 непрерывна в промежутке
непрерывна в промежутке
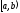 и неограниченна на этом промежутке.
и неограниченна на этом промежутке.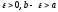 .
.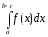 существует, т.к.
существует, т.к.
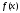 непрерывна на отрезке
непрерывна на отрезке
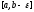 .
.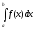 определяется следующим равенством
определяется следующим равенством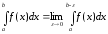 .
. непрерывна в промежутке
непрерывна в промежутке
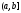 и неограниченна на нем, то несобственный
интеграл
и неограниченна на нем, то несобственный
интеграл
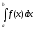 определяется аналогично предыдущему
интегралу:
определяется аналогично предыдущему
интегралу: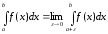 ,
где
,
где
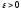 ;
;
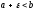 .
.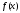 непрерывна на множестве
непрерывна на множестве
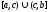 и неограниченна на этом множестве.
и неограниченна на этом множестве.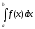 определяется следующим равенством:
определяется следующим равенством: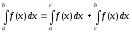 ,
если оба интеграла справа существуют.
,
если оба интеграла справа существуют. непрерывна в интервале
непрерывна в интервале
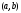 и неограниченна на этом интервале.
и неограниченна на этом интервале.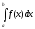 определяется равенством:
определяется равенством: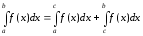 ,
где a<c<b,
при этом оба интеграла в правой части
должны существовать, т.е. должны
сходиться.
,
где a<c<b,
при этом оба интеграла в правой части
должны существовать, т.е. должны
сходиться.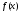 задана и непрерывна на промежутке
задана и непрерывна на промежутке
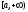 .
.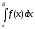 ,
этот интеграл существует
,
этот интеграл существует
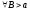 ,
т.к.
,
т.к.
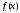 непрерывна на отрезке
непрерывна на отрезке
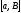 .
.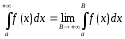 .
(1)
.
(1)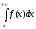 называется несобственным интегралом.
Если предел в равенстве (1) существует,
то говорят, что несобственный интеграл
сходится. Если предел в равенстве (1)
не существует, то говорят, что
несобственный интеграл расходится.
называется несобственным интегралом.
Если предел в равенстве (1) существует,
то говорят, что несобственный интеграл
сходится. Если предел в равенстве (1)
не существует, то говорят, что
несобственный интеграл расходится.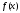 задана и непрерывна на промежутке
задана и непрерывна на промежутке
 .
.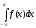 определяется аналогично:
определяется аналогично: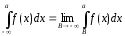
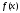 задана и непрерывна на всей числовой
оси
задана и непрерывна на всей числовой
оси
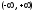 .
.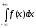 определяется следующим образом:
определяется следующим образом: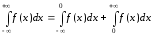 ,
, и его значение не изменится.
и его значение не изменится.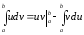 .
.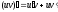 .
.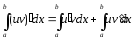
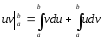
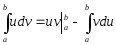 .
.
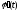 непрерывна
на отрезке
непрерывна
на отрезке
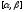 и
и
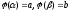 ,
а функция
,
а функция
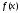 непрерывна на отрезке
непрерывна на отрезке
 .
.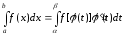 .
.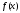 непрерывна на
непрерывна на
 ,
то она на этом отрезке имеет
первообразную, которую обозначим
,
то она на этом отрезке имеет
первообразную, которую обозначим
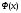 .
.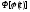 является первообразной для функции
является первообразной для функции
 на отрезке
на отрезке
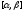 .
.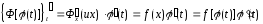 ,
где
,
где
 .
.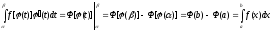 .
.
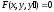 .
. и
и
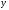 ,
но обязательно должна входить
производная
,
но обязательно должна входить
производная
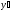 .
.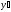 ,
то его можно представить в следующем
виде:
,
то его можно представить в следующем
виде:
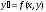
 ,
которое удовлетворяет начальному
условию
,
которое удовлетворяет начальному
условию
 .
.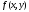 и ее частная производная
и ее частная производная
 непрерывны в некоторой области,
содержащей внутри точку
непрерывны в некоторой области,
содержащей внутри точку
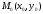 ,
то уравнение
,
то уравнение
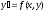 имеет
единственное решение, удовлетворяющее
начальному условию
имеет
единственное решение, удовлетворяющее
начальному условию
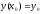 ,
в некотором интервале
,
в некотором интервале
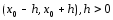 ,
т.е. задача Коши имеет единственное
решение.
,
т.е. задача Коши имеет единственное
решение.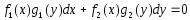 называется уравнением с разделяющимися
переменными.
называется уравнением с разделяющимися
переменными.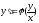 называется однородным.
называется однородным.
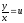 сводится к решению дифуравнения с
разделяющимися переменными.
сводится к решению дифуравнения с
разделяющимися переменными. ,
,
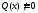 .
.
 ,
,
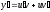 .
Значения для
.
Значения для
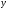 и
и
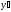 подставим в данное уравнение. В
результате получим тождество:
подставим в данное уравнение. В
результате получим тождество:
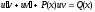
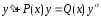
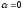 ,
то уравнение (7) является линейным.
Если
,
то уравнение (7) является линейным.
Если
 ,
то уравнение (7) является уравнением
с разделяющимися переменными.
,
то уравнение (7) является уравнением
с разделяющимися переменными.