
ЭКЗАМЕН
.docx
|
Дифференциальные уравнения 2го порядка. В общем случае
дифуравнение 2го порядка имеет вид:
Если
уравнение разрешено относительно
второй производной, то оно имеет
следующий вид:
Задача Коши для уравнения 2го порядка. Теорема Коши о существовании и единственности рашения задачи Коши. Задача
Коши: Найти решение уравнения
Теорема
Коши: Если
Определение: Всякое решение задачи Коши называется частным решением дифуравнения. Определение: Совокупность всех частных решений называется общим решением дифуравнения. Общее решение дифуравнения 2го порядка зависит от двух произвольных постоянных.
|
|
Уравнение
не содержит в явном виде
Если найти общее решение полученного
уравнения, то оно запишется в виде
Так как
Если решить последнее уравнение, то
общее решение запишется в виде
|
|
Уравнение
не содержит в явном виде
В
этом случае делается замена
|
|
Определение:
Линейно независимая система
решений
Теорема:
Для того, чтобы система решений
Доказательство: 1)Необходимость.
Дано: система
Доказательство
проведем от противного. Предположим,
что
2) Достаточность.
Дано:
Доказательство.
Предположим, что система
тогда
Достаточность доказана, а вместе с этим доказана и теорема. Проверять
фундаментальность системы решений
|
|
Определитель Вронского и его свойства. Определителем
Вронского или кратко вронскианом
системы двух частных решений
Теорема:
Если
Доказательство.
По условию теоремы
Теорема:
Если
Доказательство.
Теорема:
Вронскиан двух частных решений
тождественно равен нулю тогда и только
тогда, когда система решений
|
|
Основная теорема о структуре общего решения Л.О.Д.У. Теорема: Общее решение Л.О.Д.У. может быть записано в виде линейной комбинации фундаментальной системы решений y1(х) и у2(х), т.е. у=с1*у1(х)+с2*у2(х) Доказательство.
Пусть для Л.О.Д.У. у’’+Р(х)*у’+Q(х)*у=0
известна фундаментальная система
решений у1(х) и у2(х). Данное
уравнение можно записать в виде L(у)=0,
где L(у)=у’’+Р(х)*у’+Q(х)*у
-линейный оператор. Вначале покажем,
что у(х) =с1*у1(х)+с2*у2(х)
является решением данного уравнения.
Имеем L(у)=L(с1*у1(х)+с2*у2(х))=c1*L(y1)+c2*L(y2) у(х) =с1*у1(х)+с2*у2(х) можно получить любое решение задачи Коши. Рассмотрим задачу Коши с начальными условиями уlх=хо=у0, у’lх=хо=у0’ Положим х=х0, тогда получим:
Мы получили систему линейных уравнений относительно неизвестных с1 и с2. Определитель этой системы
Следовательно,
данная система линейных уравнений
имеет единственное решение, которое
можно найти по формулам Крамера
Итак, у(х)=
|
|
Нахождение второго частного решения Л.О.Д.У. по известному первому решению. Имеем:
где W(x)-вронскиан системы решений у1(х), у2(х). По формуле Остроградского-Лиувилля W(x)=W(x0) где W(x0) играет роль производной постоянной. Положим W(x0)=1, это скажется на виде подбираемого решения. Равенство (5) можно записать в следующем виде:
Отметим,
что
Пример
2: Найти
общее решение уравнения Решение.
Одно частное решение найдем методом
подбора. Легко проверить, что одним
из решений является функция
Общее
решение данного уравнения будет иметь
вид: y=c1x
+ Отметим,
что коэффициент -
|
|
Формула Остроградского-Лиувилля. Пусть
Умножая первое тождество на y2 , второе на y1 и складывая, получим тождество:
Учитывая,
что
Это означает, что определитель Вронского является решением дифференциального уравнения первого порядка с разделяющимися переменными z’(x)+P(x)Z(x)=0 или
Разделяя переменные и интегрируя, получим :
где х0 произвольное значение в рассматриваемом промежутке.
Потенцируя последнее равенство, получим: |z(x)|=|z(x0)| Так как х0 принимает произвольное значение, то z(x0) играет роль произвольной постоянной. Но W(x) является одним из решений уравнения (4), поэтому |W(x)|=|W(x0)| Так как Р(х)
непрерывная функция, то
Поэтому
формулы Остроградского-Лиувилля
вытекает следующее свойство определителя
Вронского: определитель Вронского
двух решений линейного однородного
дифференциального уравнения 2-го
порядка либо тождественно равен нулю
(если W(x)=0),либо
не обращается в нуль ни при одном
значении х (если W(x0)
|
|
Метод подбора частного решения Л.Н.Д.У. 2-го порядка с постоянными коэффициентами и специальной правой частью. Решение линейного неоднородного дифференциального уравнения 2го порядка с постоянными коэффициентами и специальной правой частью
где а-const,b-const, Pn(x) и Qm(x)-многочлены соответственно степеней n и m. Общее решение такого уравнения записывается в виде y=ȳ(x)+y*(x), где ȳ(x) – общее решение соответствующего однородного уравнения. |
|
Теорема о наложении частных решений. Пусть дано линейное неоднородное дифференциальное уравнение вида:
Если y*1(x) есть частное решение уравнения
а y*2(x) есть частное решение уравнения
то y*(x)= y*1(x)+ y*2(x) есть частное решение данного уравнения. Доказательство. Данное уравнение запишем в виде L(y)= f1(x)+ f2(x); где
L(y*1+
y*2)= L(y*1)+
L(y*2)
|
|
Основная теорема о структуре общего решения Л.Н.Д.У. Теорема:
Общее решение линейного неоднородного
дифференциального уравнения может
быть представлено в виде суммы общего
решения соответствующего однородного
уравнения и некоторого частного
решения данного неоднородного решения,
т.е. y(x) =
Доказательство. Во-первых,
докажем, что y(x)
=
В
самом деле, L( Во-вторых,
докажем, что y(x)
=
Рассмотрим
задачу Коши с начальным условием
Учитывая, что y(x) = C1y1(x) + C2y2(x), где y1(x) и y2(x) образуют фундаментальную систему решений, будем иметь: y(x) = C1(x) + C2y2(x) + y* (x) y’(x) = C1y1’(x) + C2y2’(x) + y*’(x) Полагая x = x0, получим систему линейных уравнений относительно неизвестных C1 и C2 y(x0) = C1y1(x0) + C2y2(x0) + y* (x0) y(x0) = C1y1’(x0) + C2y2’(x0) + y*’(x0) или C1y1(x0) + C2y2(x0) = y0 – y* (x0) C1y1’(x0) + C2y2’(x0) = y0’ – y*’(x0)
Определитель
системы =
т.к. y1(x) и y2(x) образуют фундаментальную систему решений уравнения L(y) = 0. Поэтому систему уравнений можно решить по формулам Крамера:
С10
=
Теорема доказана.
|
|
Метод вариации произвольных постоянных (метод Лагранжа) нахождения частного решения линейного неоднородного дифференциального уравнения. По
теореме
об
основной
структуре общего решения Л.Н.Д.У.
общее
решение линейного неоднородного
дифференциального уравнения имеет
вид: y(x)
=
Будем
предполагать, что
Частное решение линейного неоднородного уравнения будем искать в виде y* (x) = C1(x)y1(x) + C2(x)y2(x), где C1(x) и C1(x) - неизвестные функции. Функция y* (x) должна быть решением уравнения y” + P(x)y’ + Q(x)y = f(x). Это значит, что при подстановке y* (x), y*’(x), y*”(x) в последнее уравнение, уравнение должно обратиться в тождество.
Для нахождения
Определитель
этой системы
Неизвестные
Следовательно,
|


 .
. ,
удовлетворяющее начальным условиям:
,
удовлетворяющее начальным условиям:
 .
. непрерывна вместе с частными производными
непрерывна вместе с частными производными
 в некоторой окрестности точки
в некоторой окрестности точки
 ,
то уравнение
,
то уравнение
 имеет единственное решение в некотором
промежутке
имеет единственное решение в некотором
промежутке
 ,
которое удовлетворяет начальным
условиям
,
которое удовлетворяет начальным
условиям
 ,
т.е. задача Коши имеет единственное
решение.
,
т.е. задача Коши имеет единственное
решение.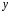 ,
т.е. уравнение имеет вид
,
т.е. уравнение имеет вид
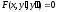 .
Сделаем замену:
.
Сделаем замену:
 ,
тогда
,
тогда
 .
В результате замены получим уравнение
первого порядка относительно неизвестной
функции
.
В результате замены получим уравнение
первого порядка относительно неизвестной
функции
 .
. .
. ,
то получаем дифуравнение первого
порядка относительно неизвестной
функции
,
то получаем дифуравнение первого
порядка относительно неизвестной
функции
 .
. .
Это будет общим решением данного
уравнения.
.
Это будет общим решением данного
уравнения. ,
т.е. уравнение имеет вид:
,
т.е. уравнение имеет вид:

 ,
,
 .
В результате замены получим уравнение
первого порядка относительно неизвестной
функции
.
В результате замены получим уравнение
первого порядка относительно неизвестной
функции
 :
:
 .
Если найдем общее решение полученного
уравнения, то оно запишется в виде
.
Если найдем общее решение полученного
уравнения, то оно запишется в виде
 .
Учитывая, что
.
Учитывая, что
 ,
получим дифуравнение первого порядка
относительно искомой функции
,
получим дифуравнение первого порядка
относительно искомой функции
 :
:
 .
Если решим полученное уравнение, то
его общее решение запишется в виде:
.
Если решим полученное уравнение, то
его общее решение запишется в виде:
 .
Это решение и будет искомым решением
данного дифуравнения.
.
Это решение и будет искомым решением
данного дифуравнения. уравнения
уравнения
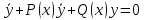 называется фундаментальной
системой решений.
называется фундаментальной
системой решений. уравнения
уравнения
 была
фундаментальной необходимо и достаточно,
чтобы отношение
была
фундаментальной необходимо и достаточно,
чтобы отношение

 фундаментальна. Доказать:
фундаментальна. Доказать:
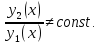
 ,
тогда
,
тогда
 .
В последнем тождестве коэффициент
при
.
В последнем тождестве коэффициент
при
 равен
равен
 .
Поэтому система функций
.
Поэтому система функций
 линейно зависима, а поэтому не является
фундаментальной. Это противоречит
условию, что и доказывает необходимость.
линейно зависима, а поэтому не является
фундаментальной. Это противоречит
условию, что и доказывает необходимость. .
Требуется доказать: система решений
.
Требуется доказать: система решений
 является фундаментальной.
является фундаментальной. не является фундаментальной, т.е. она
является линейно зависимой. Это
означает, что существуют числа
не является фундаментальной, т.е. она
является линейно зависимой. Это
означает, что существуют числа
 ,
, одновременно не равные нулю такие,
что
одновременно не равные нулю такие,
что .Пусть
для определенности
.Пусть
для определенности
 ,
, ,
что противоречит условию.
,
что противоречит условию. уравнения
уравнения
 можно
с помощью определителя Вронского.
можно
с помощью определителя Вронского. уравнения
уравнения
 называется функциональный определитель
называется функциональный определитель

 не образуют фундаментальную систему
решений уравнения (3),то
не образуют фундаментальную систему
решений уравнения (3),то
 .
. не образуют фундаментальную систему,
поэтому
не образуют фундаментальную систему,
поэтому
 ,
где С – число. Отсюда
,
где С – число. Отсюда
 .
. .
.
 ,
то
,
то
 не образуют фундаментальную систему
решений.
не образуют фундаментальную систему
решений.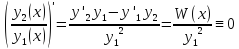
 из теоремы 4 и 5 следует :
из теоремы 4 и 5 следует : - не является фундаментальной.
- не является фундаментальной. 0,
т.к. L(y1)
0,
т.к. L(y1) 0
и L(y2)
0
и L(y2) 0
в силу того, что y1(х)
и у2(х) являются решением данного
Л.О.Д.У. Остается доказать, что
у(х) =с1*у1(х)+с2*у2(х)
является общим решением данного
уравнения, т.е. надо доказать, что из
решения
0
в силу того, что y1(х)
и у2(х) являются решением данного
Л.О.Д.У. Остается доказать, что
у(х) =с1*у1(х)+с2*у2(х)
является общим решением данного
уравнения, т.е. надо доказать, что из
решения
 =
w(x0)≠0,
т.к. система решений у1(х) и у2(х)
является фундаментальной.
=
w(x0)≠0,
т.к. система решений у1(х) и у2(х)
является фундаментальной. =
= ,
,
 =
=
 *у1(х)+
*у1(х)+ *у2(х) является решением поставленной
задачи Коши. Теорема доказана.
*у2(х) является решением поставленной
задачи Коши. Теорема доказана. =
= =
= ,
(5)
,
(5) ,
, =
= или
или
 =
= ,
,
 =
= (6)
(6) ≠const,
поэтому y1(х)
и у2(х)
образуют фундаментальную систему
решений.
≠const,
поэтому y1(х)
и у2(х)
образуют фундаментальную систему
решений.
 Второе частное решение найдем, используя
формулу (6)
Второе частное решение найдем, используя
формулу (6)
 .
. содержится в с2.
содержится в с2. два частных решения Л.О.Д.У. (3), в котором
функция Р(х) предполагается непрерывной
в некотором промежутке, тогда
два частных решения Л.О.Д.У. (3), в котором
функция Р(х) предполагается непрерывной
в некотором промежутке, тогда


 , а
, а
 y’1y’2+
y1y’’2
– y’2y’1
– y2y’’1
=
y’1y’2+
y1y’’2
– y’2y’1
– y2y’’1
=
 , получим :
, получим : .
.




 не обращается в нуль, как показательная
функция непрерывного аргумента.
не обращается в нуль, как показательная
функция непрерывного аргумента.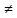 0).
0).

 ,
(7)
,
(7)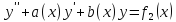 ,
(8)
,
(8) – линейный дифференциальный оператор.
Так как по условию y*1(x)
есть частное решение уравнения (7), а
y*2(x)
есть частное решение уравнения (8), то
L(y*1)
– линейный дифференциальный оператор.
Так как по условию y*1(x)
есть частное решение уравнения (7), а
y*2(x)
есть частное решение уравнения (8), то
L(y*1) f1(x)
, L(y*2)
f1(x)
, L(y*2) f2(x).
Отсюда следует тождество
f2(x).
Отсюда следует тождество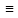 f1(x)+
f2(x).
Теорема доказана.
f1(x)+
f2(x).
Теорема доказана. + y*(x) , где
+ y*(x) , где
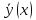 - общее решение соответствующего
однородного уравнения L(y)
= 0, а y*(x)
– частное решение данного уравнения
L(y) = f(x).
- общее решение соответствующего
однородного уравнения L(y)
= 0, а y*(x)
– частное решение данного уравнения
L(y) = f(x). + y*(x) есть
решение уравнения L(y)
= f(x).
+ y*(x) есть
решение уравнения L(y)
= f(x). +y*)
= L(
+y*)
= L( )
+ L(y*) =
F(x), т. к
L(
)
+ L(y*) =
F(x), т. к
L( )
= 0 в силу того, что
)
= 0 в силу того, что
 есть решение линейного однородного
уравнения L(y)
= 0 , а L(y*)
= F(x) в
силу того, что y* есть
решение неоднородного уравнения L(y)
= f(x).
есть решение линейного однородного
уравнения L(y)
= 0 , а L(y*)
= F(x) в
силу того, что y* есть
решение неоднородного уравнения L(y)
= f(x). + y*(x) есть
общее решение уравнения L(y)
= f(x). Для
этого надо доказать, что решение
y(x) =
+ y*(x) есть
общее решение уравнения L(y)
= f(x). Для
этого надо доказать, что решение
y(x) =
 + y*(x)
содержит любое решение задачи Коши.
+ y*(x)
содержит любое решение задачи Коши. = y0,
= y0,
 =
y0’
=
y0’ = W(x0)
= W(x0)
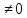
 ;
С20 =
;
С20 = ;
и функция y(x)
= С10y1(x)
+ С20y2(x)
+ y* (x) будет
являться решением задачи Коши.
;
и функция y(x)
= С10y1(x)
+ С20y2(x)
+ y* (x) будет
являться решением задачи Коши. (x)
+ y*(x),
где
(x)
+ y*(x),
где
 (x)
- есть общее решение соответствующего
однородного уравнения y”
+ P(x)y’
+ Q(x)y
= 0, а y*(x)
есть частное решение данного
неоднородного уравнения y”
+ P(x)y’
+ Q(x)y
= f(x).
(x)
- есть общее решение соответствующего
однородного уравнения y”
+ P(x)y’
+ Q(x)y
= 0, а y*(x)
есть частное решение данного
неоднородного уравнения y”
+ P(x)y’
+ Q(x)y
= f(x). (x)
известно, т.е.
(x)
известно, т.е.
 (x)
= C1y1(x)
+ C2y2(x),
где y1(x)
и y2(x)
образуют фундаментальную систему
решений Л.О.Д.У., а C1
и C2 – произвольные
постоянные.
(x)
= C1y1(x)
+ C2y2(x),
где y1(x)
и y2(x)
образуют фундаментальную систему
решений Л.О.Д.У., а C1
и C2 – произвольные
постоянные.
 и
и
 получаем
систему линейных уравнений
получаем
систему линейных уравнений

 т.
к
т.
к
 и
и
 образуют
фундаментальную систему решений
Л.О.Д.У
образуют
фундаментальную систему решений
Л.О.Д.У и
и можно
найти по формулам Крамера.
можно
найти по формулам Крамера. ;
; ;где
;где
 ,
,
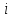 =1,2
получается из
=1,2
получается из
 заменой
заменой
 -того столбца свободными членами.
-того столбца свободными членами. ;
;

