
- •1.Метод перемещений: порядок решения задачи.
- •2. Метод перемещений: основная и эквивалентная системы.
- •9. Особенности метода перемещений в случае симметрично нагруженных симметричных конструкций.
- •10. Особенности метода перемещений в случае кососимметрично нагруженных симметричных конструкций.
- •11. Метод конечных элементов: понятие глобальной и локальной моделей. Основные гипотезы и предположения. Правило знаков.
- •13. Метод конечных элементов для плоских стержневых конструкций: порядок решения задачи.
- •19. Элементы теории упругости: теория деформированного состояния, понятие вектора перемещений и тензора деформаций.
- •20. Элементы теории упругости: вывод тензора деформаций Коши.
- •21. Элементы теории упругости: соотношения сплошности Сен-Венана.
- •22. Элементы теории упругости: теорема о напряженном состоянии. Статические граничные условия. Смягчение статических граничных условий.
- •23. Элементы теории упругости: матрица преобразования координат. Преобразование векторов и тензоров при поворотах систем координат.
- •24. Основные гипотезы о материале. Физические соотношения.
- •25. Элементы теории упругости: вывод уравнений равновесия.
- •26. Элементы теории упругости: основные соотношения теории упругости. Классификация задач теории упругости.
- •27. Элементы теории упругости: основные соотношения теории упругости в случае плоской задачи.
- •28. Элементы теории упругости: классификация прямых задач теории упругости. Метод решения прямых задач. Полу обратный метод Сен-Венана.
- •29. Элементы теории упругости: классификация обратных задач теории упругости и порядок их решения.
- •30. Элементы теории упругости: задача в перемещениях. Вывод уравнений Ламе.
- •31. Элементы теории упругости: выражение для удельной потенциальной энергии деформации.
- •32. Элементы теории упругости: возможное деформированное состояние. Вариационный принцип Лагранжа.
- •33. Элементы теории упругости: основы вариационного исчисления. Вывод уравнений Даламбера-Эйлера.
- •34. Приближенные методы: приближенный метод определения матрицы жесткости на основе вариационных принципов.
- •35. Приближенные методы: интерполяция функций полиномами Лагранжа.
- •Рекурсивное вычисление коэффициентов
- •36. Приближенные методы: интерполяция функций полиномами Эрмита.
- •37. Приближенные методы: понятие метода сеток. Запись основных дифференциальных операторов в методе сеток.
35. Приближенные методы: интерполяция функций полиномами Лагранжа.
Уравнение для определения интерполяционного полинома можно записать в детерминантной форме:

Представив последний столбец в виде суммы, получим отсюда:

Теперь разложим определитель из числителя по последнему столбцу и вспомним выражение определителя Вандермонда. Обозначим
![]()
![]()
Тогда интерполяционный полином в форме Лагранжа записывается в виде:

![]()
![]()
Образно говоря, каждое слагаемое в форме Лагранжа «отвечает» исключительно только за свой узел интерполяции (т.е. обеспечивает в нем нужное значение полинома) — и при этом «не портит» остальные узлы (обращается в них в нуль).
Пример.Построить интерполяционный полином по таблице

и
с его помощью интерполировать значение
неизвестной функции при
![]() .
.
Решение.Имеем:![]() ,
и полином в форме Лагранжа:
,
и полином в форме Лагранжа:
![]()
![]()
Подставляем
сюда
![]() :
:
Ответ.![]() .
.
Рекурсивное вычисление коэффициентов
Теорема.Пусть числа![]() все
различны. Для полинома
все
различны. Для полинома![]() справедливы
следующиеравенства Эйлера–Лагранжа:
справедливы
следующиеравенства Эйлера–Лагранжа:

Теорема.Обозначим

Имеют
место равенства, связывающие коэффициенты
интерполяционного полинома![]() с
величинами
с
величинами![]() и
и![]() :
:
![]()
Формулы
позволяют рекурсивно, начиная со
старшего, вычислить коэффициенты
интерполяционного полинома по величинам
![]() и
и![]() .
.
Пример.Найти корни интерполяционного полинома, заданного таблицей

Решение.Здесь![]() ,
,
![]()
![]()
![]()
![]()

![]()
![]()
Формулы:

Уравнение
![]() легко
решается подстановкой
легко
решается подстановкой![]() .
.
Ответ.![]() .
.
36. Приближенные методы: интерполяция функций полиномами Эрмита.
Задача
[Эрмит].
Построить полином
![]() ,
имеющий заданные значения своих
производных в узлах интерполяции
,
имеющий заданные значения своих
производных в узлах интерполяции![]() :
:

При
![]() узел
узел![]() называетсяпростым
узлом интерполяции,
при
называетсяпростым
узлом интерполяции,
при
![]() узел
узел![]() называетсякратным
узлом.
называетсякратным
узлом.
Для
случая вещественной интерполяционной
таблицы (
![]() )
задаче можно придать следующую
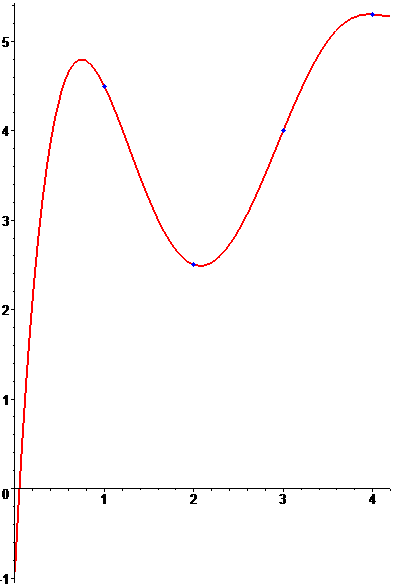
геометрическую интерпретацию: требуется
провести алгебраическую кривую
)
задаче можно придать следующую
геометрическую интерпретацию: требуется
провести алгебраическую кривую![]() через
заданные точки
через
заданные точки![]() так,
чтобы в каждой точке обеспечить заданные
наклоны касательных (а также, возможно,
кривизны и т.п.).
так,
чтобы в каждой точке обеспечить заданные
наклоны касательных (а также, возможно,
кривизны и т.п.).

§
Интерполяционный полином Эрмита используется в задаче разложения дробно-рациональной функции на простейшие дроби. Сам Эрмит применял его для оценки величины определенного интеграла по значениям функции и ее производных на концах интервала. Еще одно приложение — в задаче вычисления функции от матрицы.
Интерполяционная
таблица дает
![]() условий
на коэффициенты неизвестного полинома.
По аналогии состандартной
задачей интерполяции,
можно ожидать, что искомый полином будет
существовать среди полиномов степени
условий
на коэффициенты неизвестного полинома.
По аналогии состандартной
задачей интерполяции,
можно ожидать, что искомый полином будет
существовать среди полиномов степени
![]() .
Будем искать этот полином методом
неопределенных коэффициентов. Обозначим
.
Будем искать этот полином методом
неопределенных коэффициентов. Обозначим
![]()

Пусть
![]() —
произвольный полином степени
—
произвольный полином степени![]() .
Разложим дробь
.
Разложим дробь![]() насумму
простейших
над множеством
насумму
простейших
над множеством
![]() :
:

Определим
числители дробей
![]() с
помощью интерполяционных данных.
Домножим обе части тождества на
с
помощью интерполяционных данных.
Домножим обе части тождества на![]() ,
получим:
,
получим:

здесь
через
![]() обозначена
дробно-рациональная функция по
обозначена
дробно-рациональная функция по![]() ,
знаменатель которой не обращается в
нуль при
,
знаменатель которой не обращается в
нуль при![]() .
Подставим это значение
.
Подставим это значение![]() в
обе части последнего равенства:
в
обе части последнего равенства:

Теперь
продифференцируем последнее тождество
по
![]() ,
подставим
,
подставим![]() и
воспользуемся данными интерполяционной
таблицы:
и
воспользуемся данными интерполяционной
таблицы:
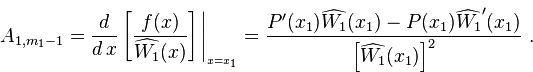
Снова
продифференцируем по
![]() и
т.д. В результате получаем:
и
т.д. В результате получаем:

Аналогично поступаем и с другими узлами интерполяции. В результате, получаем решение задачи в виде интерполяционного полинома Эрмита:

В литературе имеется неоднозначность терминологии — этот же полином называется и интерполяционным полиномом Лагранжа-Сильвестра, и интерполяционным полиномом Серре.
Теорема.
Подмножество
всевозможных полиномов из
![]() ,принимающих
значения по таблице, можно представить
в виде
,принимающих
значения по таблице, можно представить
в виде
![]()
здесь
![]() —интерполяционный
полином Эрмита.
—интерполяционный
полином Эрмита.
Интерполяционный
полином Эрмита является естественным
обобщением обычного интерполяционного
полинома в форме
Лагранжа
(
![]() )
иформулы
Тейлора
(
)
иформулы
Тейлора
(
![]() ).
).
Можно указать и явное представление для этого полинома — с использованием формализма определителей. На основании правила дифференцирования дробно-рациональной функции, получаем:

Здесь
![]() —биномиальный
коэффициент.
Еще один подход к построению полинома
см. ☞
[8].
—биномиальный
коэффициент.
Еще один подход к построению полинома
см. ☞
[8].
П
Пример. Построить интерполяционный полином по таблице

Решение. Здесь
![]()
Для
![]() имеем
имеем![]() и
в формуле Эрмита этому узлу соответствует
одно слагаемое:
и
в формуле Эрмита этому узлу соответствует
одно слагаемое:
![]()
Для
![]() имеем
имеем![]() и
этому узлу соответствует полином
и
этому узлу соответствует полином
![]()
значения
которого — вместе с первой и второй
производной — в точке
![]() должны
совпадать с табличными:
должны
совпадать с табличными:
![]()
![]()
![]()
Для
![]() имеем
имеем![]() :
:

и для определения четырех коэффициентов этого полинома мы имеем четыре условия из таблицы:
![]()
![]()
![]()
![]()
Этот же результат можно получить и в виде альтернативного — детерминантного — представления:
![]()
и

Наконец,
для
![]() имеем
имеем![]() :
:
![]()
Ответ.
![]() .
.
Построить
уравнение «горки»: найти полином из
условий
![]() .
.
Следующий результат не очень связан с содержанием настоящего пункта, но надо было куда-то поместить.
Теорема
[1].
При
заданных
![]() существуют
а)
полином
существуют
а)
полином
![]()
(т.е.
![]() )и
б)
числа
)и
б)
числа
![]() такие,
что
такие,
что
![]()
