9. Особенности метода перемещений в случае симметрично нагруженных симметричных конструкций.
см. 10
10. Особенности метода перемещений в случае кососимметрично нагруженных симметричных конструкций.
В большинстве случаев конструкции симметричны, нагрузка может быть симметрична и несимметрична.
Благодаря наличию прямой или косой симметрии количество неизвестных в методе перемещений может быть уменьшено. В симметричной конструкции, нагруженной симметричным образом, перемещения симметрично расположенных узлов симметричны.
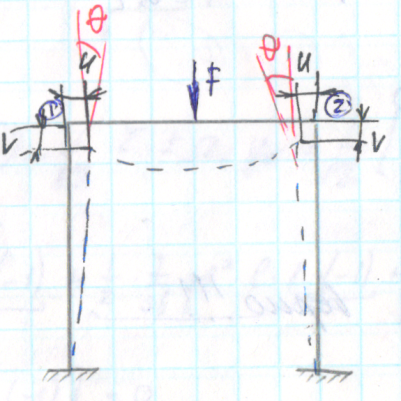
Редакция Соскова:
мы сразу задаем два перемещения так как они одинаковы и считаем коэффициенты от действия совместного их воздействия
это ответ на оба вопроса
различие только в направлениях перемещений...
В симметричных конструкциях , нагруженных кососимметричным образом симметричные обобщённые перемещения (обобщённый перемещения симметричных узлов) обладает косой симметрией
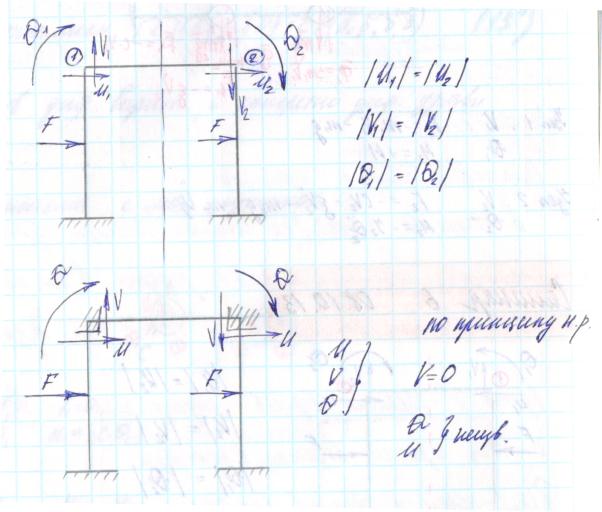При
записи канонического уравнения при
наличии симметрии, каждое уравнение
отвечает суммарной силе,действующей
одновременно в 2х симметричных узлах.
При составлении матрицы жёсткости и
определении обобщённой силы слагаемые,
соответствующие симметричным узлам,
суммируются.
11. Метод конечных элементов: понятие глобальной и локальной моделей. Основные гипотезы и предположения. Правило знаков.
Понятия глобальной и локальных моделей определяются в ведением общей системе координат для всех элементов системы и определением ориентации каждого элемента относительно этой системы координат, а также влияние коэффициентов жесткости для перемещений принятых в глобальной системе координат (вводит для однозначного определения влияния каждого элемента системы на другие элементы системы).Так для каждого элемента локальной матрицы жесткости преподается свое место в глобальной матрице жесткости :
,
где
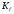-глобальная
матрица жесткости,
,
,
,
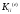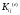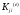-локальные
матрица жесткости для элемента
находящегося междуi
и j
- узлами.
L - матрицы перехода из локальной системы координат в глобальную
В рамках курса применяются применяются следующие допущения и гипотезы:
-однородность материала
-гипотезы сплошности
-гипотезы изотропности
-гипотеза деформируемости (принцип малых размеров)
-гипотеза идеальной упругости материала при произвольных нагрузках, выполняется закон Гука.
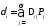-принцип
возможных напряженных состояний. Принцип
Постеляма.
Принцип Сен-Винана: в зонах в дали точки приложения силы ее характер (распределеность) можно не учитывать.
Принцип упругой эквивалентности
Правило знаков определяется согласно правой системе координат.
12. Метод конечных элементов для фермовых конструкций: порядок решения задачи.
Порядок указан в МКЭ, в задачах учитываются только растягивающие усилия, и задачи рассчитываются только на растяжение.
13. Метод конечных элементов для плоских стержневых конструкций: порядок решения задачи.
Порядок указан в МКЭ, в задачах учитываются только изгибающие силы, т.к. силы которые должны вызвать растяжение на несколько порядков превышают изгибающие силы (стержни лучше работают на изгиб, чем на растяжение).
14. Метод прямых жесткостей: определение функций формы и коэффициентов матрицы жесткости для стержневого конечного элемента, работающего на растяжение-сжатие и кручение.
15. Метод прямых жесткостей: определение функций формы и коэффициентов матрицы жесткости для нерастяжимого стержневого конечного элемента, работающего на изгиб
16. Метод конечных элементов: схематизация способов закрепления. Учет способа закрепления при составлении канонической системы МКЭ.
Редакция Соскова:
там перечислить виды заделок и сказать о замене уравнений статики уравнениями кинематики
ну еще куча всякой мелочи
17. Метод конечных элементов: решение канонической системы методом Гаусса.
Заключается в линейном преобразование совместной матрицы в треугольный вид:
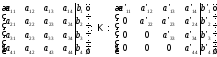
обратным ходом находим исходные перемещения.
18. Метод конечных элементов: решение канонической системы методом простых итераций и методом итераций Зейделя.
Постановка задачи
Требуется найти решение системы n линейных уравнений, которая записывается в общем виде как
;
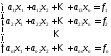Предположим,
что диагональные элементы матриц
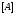исходной системы не равны 0 (aii
≠ 0, i = 1, 2, …, n). Разрешим первое уравнение
системы относительно x1,
второе относительно x2
и т.д. Получим следующую эквивалентную
систему, записанную в скалярном виде:
вычисляем последовательные приближения по формуле простой итерации:
или по методу Зейделя:
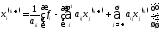
принимают,
что
,
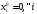а точность найденных переменных
определяется как
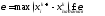, процесс итерации производят до тех
пор пока не будет достигнута заданная
точность. (Для сходимости метода
необходимо диагональное преобладание).
при решение составляют итерационные
таблицы
|
k |
x1 |
x2 |
... |
xn |
|
0 |
0 |
0 |
0 |
0 |
|
1 |
x11 |
x21 |
... |
xn1 |
|
... |
... |
... |
... |
... |
|
m |
x1m |
x2m |
... |
xnm |