19. Элементы теории упругости: теория деформированного состояния, понятие вектора перемещений и тензора деформаций.

Напряженное состояние в точке

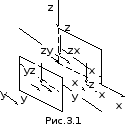
Вырежем из напряженного тела произвольной бесконечно малый параллелепипед ( рис. 3.1 ). На гранях параллелепипеда действуют нормальные и касательные напряжения. Направление нормальных напряжений совпадает с направлением внешней нормали . Касательные напряжения разложим на составляющие, параллельные осям. На невидимых гранях элемента возникают такие же напряжения, только противоположно направленные. Напряжения на гранях параллелепипеда являются компонентами тензора напряжений – Т.

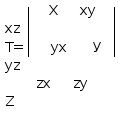
Параллелепипед находится в равновесии, выполняются все уравнения равновесия, в частности, М_х=0 . _zydxdydz -_yzdzdxdy=0. Откуда: _zy=_yz. Аналогично _zx=_xz, _xy=_yx. Эти выражения представляют собой закон парности касательных напряжений. Из закона парности касательных напряжений следует, что на гранях элемента имеем не девять, а шесть независимых компонентов тензора напряжений. При вращении параллелепипеда величины напряжений меняются. Можно добиться такого положения параллелепипеда, при котором все касательные напряжения обратятся в ноль. Грани параллелепипеда, находящиеся в этом положении, называются главными площадками, а нормальные напряжения, действующие на них, называются главными напряжениями, которые обозначаются ₁, ₂ и ₃, причем ₁₂₃.

Если два главных напряжения равны нулю, то напряженное состояние называется линейным или простым. При этом, если ₁0, то это растяжение, а если ₃0, то это сжатие. Если одно главное напряжение равно нулю, то напряженное состояние называется плоским, если все главные напряжения не равны нулю, то объемным. Плоское и объемное напряженные состояния называются сложными.

20. Элементы теории упругости: вывод тензора деформаций Коши.

Для характеристики деформации рассмотрим две точки A,B: ,,,,;,,

???

21. Элементы теории упругости: соотношения сплошности Сен-Венана.

В следствии определённости задачи теории упругости, перемещения должны восстанавливаться по компонентам тензора деформации.

Из него легко выразить:

(Выражение должно быть полным диффернециалом???)

Вторые производные тензора деформации должны быть связаны между собой.

Например:

22. Элементы теории упругости: теорема о напряженном состоянии. Статические граничные условия. Смягчение статических граничных условий.

Th: Для определения напряжения на наклонной площадке необходимо и домтаточно знание напряжений на 3х взаимоперпендикулярных площадках.

Исключай так называемые моментные напряжения будем иметь на всяких положительных гранях:

23. Элементы теории упругости: матрица преобразования координат. Преобразование векторов и тензоров при поворотах систем координат.

Формула преобразования компонент тензора (1.44) – одна из основных в тензорной алгебре!

В случае тензора n-го ранга можно говорить о симметрии или антисимметрии его компонент относительно определенной пары индексов. Тензор симметричен относительно r-го и s-го индексов, если

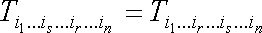         (1.45)

антисимметричен, если

     (1.46)

Свойства симметрии не зависят от выбора системы координат, т.е. тензор, симметричный или антисимметричный в одной системе, остается таким же при произвольных преобразованиях осей координат. Покажем это на примере симметричного тензора второго ранга.

Пусть  Т_ik =Т_ki,

 T^'_ik= _ilkmT_lm= _kmilT_ml=T^'_ki       (1.47)

Из семинаров:

Уравнении равновесия:

Х₁, Х₂, Х₃ – старая (основная) СК

Х₁`, Х<sub>2</sub>`, Х₃` - новая СК

Преобразование от одной СК к другой с помощью матрицы косинусов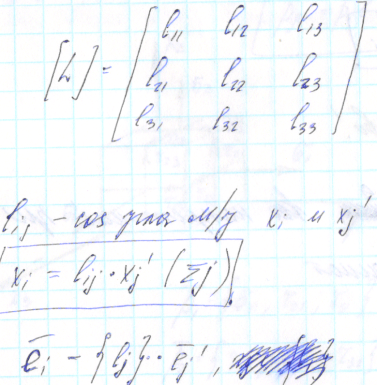

Для нахождения тензора в новой СК, найдём векторы полных напряжений, действующих на площадках, перпендикулярных осям новой СК: