7. Вопрос. Обратное преобразование Фурье.

Служит для нахождения сигнала по спектру.

Условие существования спектральной плотности сигнала. Спектральный анализ интегрируемых сигналов.

Сигнал можно сопоставить спектральную плотностьесли сигнал абсолютно интегрирован.

К абсолютно интегрированному сигналу не относятся гармонические колебания и постоянный ток.

Примеры абсолютно интегрируемых и неинтегрируемых сигналов на (рис. 16).

Спектры таких сигналов представляются через дельта-функции.

Спектр сигнала постоянного уровня А представляет собой дельта-импульс, расположенный на нулевой частоте ().

Физический смысл данного выражения – сигнал, постоянный по модулю и по времени имеет постоянную составляющую только на нулевой частоте.

- спектр синусоидального сигнала.

Любой периодический сигнал можно представить рядом Фурье в комплексной форме, то есть в виде суммы синусоидальных сигналов.

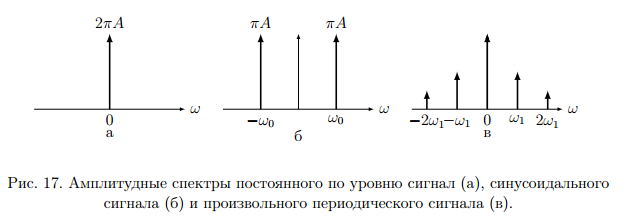
Спектры постоянного тока, синусоидального и периодического сигнала показаны на (рис. 17).

На анализаторе спектра спектр периодического сигнала будет наблюдаться в виде последовательности остроконечных импульсов. Амплитуды данных импульсов пропорциональны амплитудам гармоник. Типичный вид спектра представлен на (рис. 18).

Спектральный анализ можно применять и к случайным сигналам. Для них рассматривается спектр мощности . Для примера рассмотрим белый шум (рис. 1).

Белый шум имеет равномерный спектр, то есть выполняется условие .

8 Вопрос. Свертка аналогового сигнала.

Свертка двух сигналов иопределяется как сигнал.

Операция свертки коммутативна, то есть при перестановке ее параметров результат не меняется.

Физический смысл свертки – отклик линейной аналоговой системы на входной сигналпредставляет собой свертку входного сигнала и импульсной характеристики системы.

Преобразование Фурье от импульсной характеристики системы называется частотной характеристикой.

8. Вопрос. Дискретные сигналы.

Переход от аналогового сигнала к цифровому. Квантование сигнала

Дискретный сигнал представляет собой последовательность отсчета через некоторые промежутки времени. Отсчеты, как правило, берут через равный промежуток времени, называемый шагом дискретизацию. Отсчеты сигнала обычно представляется в некоторой ступенчатой форме. Ступенчатое представление сигнала называется дискретизацией. Дискретизация по времени называется выборкой. Дискретизация по уровню называется квантованием. Если сигнал, подвергнутый квантованию по времени и по значению затем представить в цифровом виде, то такое преобразование называется аналогово-цифровым преобразованием. Процесс дискретизации по уровню и по времени показан на (рис.26).

Каждому уровню аналогового сигнала ставится в соответствие двоичное число. В нашем примере мы используем 8 уровней квантования и трехразрядные двоичные числа. Таким образом мы перешли от аналогового сигнала к последовательности двоичных чисел. Цифровой сигнал существует только в дискретных во времени точках и может принимать в каждой сигнал с непрерывной амплитудой из точек только одно их значений, где- разрядность АЦП. Процесс аналого-цифрового преобразования состоит из следующих этапов:

1. В начале сигнал дискретизируется, то есть преобразуется в дискретный по времени.

2. Амплитуда каждого дискретного отсчета квантуется в один из уровней.- число бит, через которое АЦП представляет значение сигнала.

3. Дискретные уровни амплитуды кодируются в виде двоичных слов, каждое из которых имеет длину бит.

Операцию дискретизации аналогового сигнала можно описать, введя в рассмотрение функцию 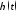. Данная функция представляет собой последовательность- импульсов, следующих через равные промежутки времени.

Осциллограмма функции показана на (рис. 27).

Операция перехода от аналогового сигнала к дискретному сводится к перемножению сигнала и дискретизирующей последовательности, вместо которой обычно используются остроконечные импульсы. Такая операция называется стробирование.

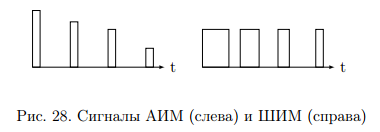
Переходными формами от аналогового сигнала к цифровым являются сигналы с импульсной модуляцией. Импульсы могут иметь одинаковую длительность, но амплитуда может быть пропорциональна отсчетным значениям дискретизированного сигнала. Такой виз преобразования называется амплитудно-импульсной модуляцией (АИМ). Если амплитуда импульсов постоянна, а их длительность пропорциональна мгновенному значению аналогового сигнала, то получается широтно-импульсная модуляция (ШИМ). ШИМ и АИМ сигнала показаны на (рис. 28).