
- •Вопрос. Радиотехнические сигналы. Классификация.
- •Аналоговые сигналы.
- •Вопрос. Модулированный сигнал. Основы модуляции.
- •Сигма и дельта функции.
- •Вопрос. Мощности и энергии сигнала.
- •Спектральный анализ сигналов.
- •Вопрос. Разложение аналогового сигнала в ряд Фурье.
- •Вопрос. Спектральные диаграммы.
- •Преобразование Фурье.
- •Свойства преобразования Фурье
- •Пример вычисления спектра импульсного сигнала.
- •Вопрос. Обратное преобразование Фурье.
- •Условие существования спектральной плотности сигнала. Спектральный анализ интегрируемых сигналов.
- •8 Вопрос. Свертка аналогового сигнала.
- •Вопрос. Дискретные сигналы.
- •10 Вопрос. Теорема Котельникова (Найквиста)
- •Спектр дискретного сигнала и наложения
- •11 Вопрос. Восстановление сигнала по отсчету
- •Ошибки квантования
- •12 Вопрос. Система цифровой обработки сигналов реального времени
- •Спектральный анализ дискретных сигналов
- •13 Вопрос. Дискретное преобразование Фурье дпф (dft)
- •Восстановление исходного сигнала из дпф.
- •14 Вопрос. Дискретная свертка
- •15 Вопрос. Свойства дпф:
- •Обратное дпф.
- •16 Вопрос. Быстрое преобразование Фурье.
- •17 Вопрос. Оконные функции.
- •18 Вопрос. Цифровые фильтры. Системы дискретного времени.
- •19 Вопрос. Z – преобразование.
- •20 Вопрос. Прохождение цифрового сигнала через систему дв.
- •21 Вопрос. Цифровые фильтры с конечной импульсной характеристикой (ких).
- •22 Вопрос. Рекурсивный фильтр (бих).
- •23 Вопрос. Канонический рекурсивный фильтр.
- •24 Вопрос. Синтез цф. Метод инвариантных импульсных характеристик.
- •25 Вопрос. Синтез цф. Метод инвариантных частотных характеристик.
- •Билинейное z – преобразование.
- •26 Вопрос. Прямые методы синтеза фильтров.
- •27 Вопрос. Dsp (Digital Signal Processing).
Преобразование Фурье.
Применяется для расширения области допустимых сигналов.
Различают прямое и обратное преобразование.
Вопрос. Прямое преобразование (переход от сигнала к спектру).
Разложение в ряд Фурье позволяет получить спектр только для периодических сигналов. Преобразование Фурье расширяет область применения спектрального анализа на непериодические сигналы.
Пусть s(t) – одиночный импульсный сигнал конечной длительности. Дополним его таким же, периодически следующим сигналом, с периодом Т. Получим последовательность импульсов (рис.15).

Чтобы перейти к
преобразованию Фурье и найти спектр
одиночного импульса необходимо найти
предельный вид ряда Фурье в комплексной
форме при

Расчет спектра:

Физический смыл спектральной плотности состоит в том, что она является коэффициентом пропорциональности между длинной малого интервала частот Δf в близи частоты f0 и амплитуды гармонического сигнала с частотой f0. Сигнал s(t) как бы складывается из множества разных синусоидальных сигналов малой амплитуды. Спектр плотности показывает вклад в сигнал элементарных синусоидальных сигналов каждой частоты.
Спектр плотности
вероятности
 является комплексным числом и отображается
кривой на комплексной плоскости.
является комплексным числом и отображается
кривой на комплексной плоскости.
 - действительное
число – амплитудный спектр
- действительное
число – амплитудный спектр
 - спектр мощности
- спектр мощности
 - фазовый спектр
- фазовый спектр
Свойства преобразования Фурье
Линейность – спектр суммы нескольких сигналов умножить на постоянные коэффициенты равен сумме этих сигналов. Если амплитуда сигнала меняется в А раз, то его спектральная плотность тоже меняется в А раз.

Свойство вещественной и мнимой частей спектра. Вещественная часть спектра, то есть амплитудный спектр – четный функция частоты. Амплитудный спектр симметричен относительно нулевой частоты. Мнимая часть спектра – нечетная функция частоты. Фазовый спектр антисимметричен относительно нулевой частоты.
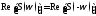

Смещение сигнала во времени. При смещении сигнала во времени амплитудный спектр не меняется, а фазовый спектр смещается по фазе.
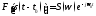
Изменение масштаба сигнала по времени. Пусть сигнал s(t) сжат по времени в k-раз. Сжатый сигнал записывается, как s(kt).

Свертка и произведение двух сигналов.
Спектр произведения сигналов равен свертке спектров и наоборот.
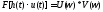
Свойство применяется для отыскания сигнала на выходе, если известна АЧХ.

Линейная система и сигналы на ее входе и выходе показаны на рисунке 20.

Спектр дельта функции.

В
спектре дельта-импульса содержатся все
частоты от 0 до
 .
.
Спектр производной и интеграла.
Дифференциация сигналов приведет к расширению спектра, интегрирование – к сжатию (рис.21).

Связь с рядами Фурье.
Комплексная
амплитуда
 к-ой гармоники ряда Фурье связана со
спектральной плотностью так:
к-ой гармоники ряда Фурье связана со
спектральной плотностью так:
Зная преобразование для одного периода периодического сигнала можно вычислить его разложение в ряд Фурье.
Пример вычисления спектра импульсного сигнала.
Вычислим спектр
прямоугольного видео импульса
 с
амплитудой
с
амплитудой и длительностью
и длительностью .
Импульс расположен симметрично
относительно начала отсчета (рис. 22).
.
Импульс расположен симметрично
относительно начала отсчета (рис. 22).


Переходим от круговой частоты к частоте f.
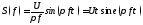
Амплитудный спектр показан на (рис 23).
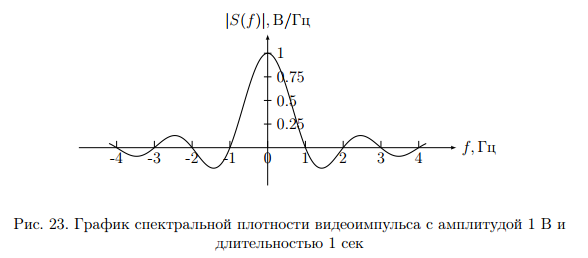
Фазовый спектр показан на (рис 24).

Спектр мощности показан на (рис 25).

