Сигма и дельта функции.

Сигма функция задается следующим выражением:

(рис. 9)

Дельта функция – импульс бесконечно большой амплитуды и бесконечно малой длительности. (рис. 10).

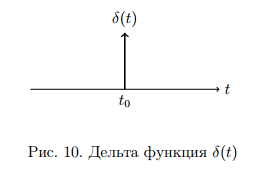
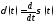- дельта-функция является производной от сигма-функции.

Если сигнал, задаваемый непрерывной функцией умножить на дельта-функции и проинтегрировать во времени, то результатом будет мгновенное значение сигнала в точке, где сосредоточен дельта-импульс.

Из фильтрующих свойств дельта-функции следует схема измерителя мгновенного значения сигнала.

Сигма и дельта функции применяются для анализа прохождения аналоговой и цифровых сигналов через линейные системы. Отклик системы, ели на нее подан дельта-импульс, называется импульсной характеристикой системы H(t).

3. Вопрос. Мощности и энергии сигнала.

Мощность выделяющаяся на резисторе сопротивлением R, если к нему приложено напряжение u определяется как W=(u^2)/R.

Если к резистору приложено не постоянное напряжение, а переменный сигнал s(t), то мощность так же будет переменной (мгновенная мощность).

В теории сигналов обычно полагают, что R=1. w=s(t) ^2. Чтобы найти энергию сигнала необходимо проинтегрировать мощность по всему диапазону;

Для бесконечных во времени сигналов среднюю мощность можно определить следующим образом:

W=[Вт], E=[(В^2)*c]

Именно такая энергия выделяется на резисторе сопротивлением 1 ом, если к нему приложено напряжение s(t).

Если сигнал излучается на некотором интервале T, то рассматривается средняя мощность сигнала.

Спектральный анализ сигналов.

4. Вопрос. Разложение аналогового сигнала в ряд Фурье.

Разложение в ряд Фурье заключается в представление периодического сигнала в виде суммы синусоидальных сигналов.

Пример представления пилообразного сигнала в виде суммы синусоидальных сигналов с различной амплитудой и фазой представлен на рис. 12.

Введем основную частоту периодического сигнала с периодом T: w_1=2pi/T. Периодический сигнал при разложении в ряд Фурье представляется в виде суммы синусоидальных сигналов или гармоник, с частотами кратными основной частоте: 2w_1, 3w_1... Амплитуды этих сигналов называются коэффициентами разложения. Ряд Фурье записывается в виде суммы гармоник:

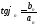
Вещественная форма ряда Фурье:

Используя известную форму записи из курса электротехники в виде комплексного числа, ряд Фурье представляется в виде:

В данное выражение входят гармоники с отрицательными частотами. Отрицательная частота – это не физическое понятие, она связана со способом представления комплексных чисел. Так как сумма гармоник должна быть действительным числом, то каждой гармонике соответствует комплексно сопряженная гармоника с –ω. По абсолютному значению амплитуды гармоники с положительными и отрицательными частотами равны.

5. Вопрос. Спектральные диаграммы.

Спектральные диаграммы – графики, изображающие коэффициенты ряда Фурье в вещественной форме.

Различают амплитудные и фазовые спектральные диаграммы. По горизонтальной оси откладывают частоты гармоник, по вертикали – амплитуды (фазы). Если изображен модуль ряда Фурье в комплексной форме, то по оси Х откладывают положительную и отрицательную круговую частоту ω.

Пример спектра аналогового периодического сигнала. (ШИМ)

Рассмотрим последовательность прямоугольных импульсов с периодом Т, длительностью τ и амплитудой А.

- скважность.

Осциллограмма такого сигнала оказана на рисунке 13.

- постоянная составляющая прямоугольного сигнала.

b_n = 0.

Спектральная диаграмма для последовательности прямоугольных импульсов показана на рис. 14.

Из спектра диаграммы видно, что с увеличением скважности уменьшается длительность импульса. Последовательность прямоугольных импульсов имеет более богатый спектральный состав, в спектре присутствуют больше гармоник и больше амплитуд. Таким образом, сокращение длительности импульса приводит к расширению спектра. Сигналы с широким спектром могут создавать помехи.

Вычисление ряда Фурье производится с помощью математических пакетов.