студ ивт 22 материалы к курсу физики / belonuchkin_ve_zaikin_da_tsipeniuk_ium_kurs_obshchei_fiziki

к плоскости орбиты, на электрон будет действовать сила Лоренца

направленная по радиусу орбиты ( 0 — индукция поля). Под действием этой силы скорость электрона изменяется и становится равной . Центростремительная сила, приложенная к электрону, становится равной

Предполагая, что под действием поля угловая частота враще-

называется ларморовой угловой частотой.

Таким образом, магнитное поле вызывает изменение угловой частоты обращения электрона по орбите, причем это изменение одинаково для всех электронов независимо от радиуса их орбит и линейных скоростей движения; по направлению Л совпадает с H.

В общем случае, когда H не перпендикулярно к плоскости орбиты, внешнее поле вызывает прецессию орбиты вокруг поля, так что нормаль к плоскости орбиты описывает конус вокруг H (см. рис. 11.3 б). Угловая скорость такой прецессии описывается той же формулой (11.10). Прецессия электронной орбиты приводит к дополнительному движению электрона вокруг поля H, налагающемуся на его орбитальное движение. По магнитному действию это дополнительное движение эквивалентно замкнутому току

(11.11)

где частота прецессии Л Л 2 ; знак «минус» отражает отрицательный заряд электрона. Элементарный ток обладает магнитным моментом

где 2 2 2 2 — средний квадрат расстояний электронов от оси , взятой в направлении магнитного поля) — площадь контура, который описывает электрон вследствие пре-

562 Магнетизм веществ [ Гл. 11

цессии вокруг поля . При сферически симметричном распреде-

лении заряда в атоме 2 2 2 и поэтому средний квадрат

расстояния электрона от ядра 2 2 2 2 3 2 2. Следовательно 2 3 2 и мы получаем, что

Из формулы (11.13) видно, что в магнитном поле каждый электрон приобретает дополнительный так называемый индуцированный магнитный момент, направленный противоположно полю H. Появление этого момента и обусловливает намагничивание тела в направлении, противоположном полю, присущее диамагнетизму.

Чтобы найти магнитную восприимчивость тела, надо просуммировать в атоме магнитные моменты всех его электронов и умножить на число атомов в единице объема. В результате получается следующее выражение для молярной восприимчивости

где — заряд ядра (число электронов в атоме), — концентрация атомов. Из полученной формулы следует, что в полном соответствии с опытом магнитная восприимчивость диамагнетиков не зависит ни от температуры, ни от напряженности поля и растет пропорционально порядковому номеру элемента .

Оценим, какова по порядку величины получается на основе этой формулы восприимчивость веществ. Пусть 10 10 м,5 1028 1/м3, тогда 10 6 , что согласуется с данными табл. 11.1.

Металлы в твердом состоянии помимо электронов, связанных с атомами, содержат также обобществленные электроны, образующие электронный газ. Магнитное поле искривляет траектории электронов, что приводит к появлению у электронного газа диамагнитных свойств, называемых диамагнетизмом свободных электронов. Как показал впервые Л.Д. Ландау, их магнитная

где — концентрация электронного газа, Б — магнетон Бора,Ф — энергия Ферми. По порядку величины дэ сравнима с диа-

магнитной восприимчивостью атомных электронов. Парамагнетизм. Вещества, атомы которых обладают неском-

пенсированным магнитным моментом, принадлежат к парамагнетикам (при температурах выше температуры магнитного упо-

11.2 ] Природа магнетизма 563

рядочения — температуры Кюри C — ферромагнетики также являются парамагнетиками, о чем пойдет речь ниже). В отсутствие внешнего магнитного поля магнитные моменты как атомов, так и свободных электронов, имеют всевозможные направления, так что суммарный магнитный момент вещества равен нулю. При наличии поля состояния, соответствующие направлению «по полю», оказываются энергетически более выгодными, и вещество намагничивается.

Рассмотрим, чем определяется восприимчивость парамагнитного вещества, в котором магнитный момент атома обусловлен только спином одного электрона. Как известно, проекция спина на любое выделенное направление (в нашем случае по направлению магнитного поля) может быть равно либо 2, либо 2. Проекция спинового магнитного момента электрона также может иметь соответственно два значения , где — абсолютное значение проекции магнитного момента.

Напомним, что для электрона направление магнитного момента противоположно направлению спина и поэтому выше написано, что проекция на ось равна «минус-плюс» . В нашем случае равно магнетону Бора: Б .

Взаимодействие магнитного момента с внешним полем приводит к дополнительной энергии , зависящей от взаимной ориентации этих векторов. Следовательно, в нашем случае в магнитном поле у атома возникают два возможных уровня энергии

и , (11.16)

причем в низкоэнергетическом состоянии магнитный момент параллелен магнитному полю.

В соответствии с формулой Больцмана отношение числа электронов с энергией к числу электронов с энергиейравно

Возможность замены экспоненты ее приближенным выражением связана с тем, что практически во всех магнитных полях магнитная энергия атомов оказывается много меньше тепловой, т. е. Б Б . Действительно, даже если 10 Тл (а такие поля получить очень трудно) и 300 K, то отношение

2 Б 0,05.

Намагниченность вещества определяется только разностью чисел электронов, ориентированных по или против поля. Эту разность легко вычислить на основе формулы (11.17):

нице объема. При написании второй части уравнения (11.18) мы не делали различия между и 0 , так как электроны дают в парамагнетике очень малый вклад в суммарное поле. Магнитный момент вещества равен поэтому

Учитывая, что магнитный момент электрона равен магнетону Бора, мы получаем следующее выражение для парамагнитной части восприимчивости:

у атома более одного электрона и суммарный угловой момент атома равен :

3 Б

В этой формуле — фактор Ланде, определяющий связь между магнитным и полным моментом системы. Как нетрудно убедиться, при 1 2 и 2 эта формула переходит в формулу (11.20).

Полученная формула, как уже указывалаось, носит название закона Кюри и показывает, что магнитная восприимчивость парамагнетиков обратно пропорциональна температуре.

Парамагнетизм свободных атомов и ионов определяется в основном полным моментом импульса электронной оболочки, характеризующимся квантовым числом , как это следует из формулы (11.21). Величина остается хорошим квантовым числом и в твердых диэлектриках, где носителями магнитных моментов являются ионы лантанидов и актинидов. Однако для ионов группы железа (Ti, V, Cr, Mn, Fe, Co, Ni, Cu) за счет сильного влияния внутрикристаллического поля происходит «замораживание» орбитального момента. Связано это с тем, что магнитные свойства ионов группы железа обусловлены внешней 3 -оболочкой в отличие от ионов лантанидов и актинидов, их магнетизм обусловлен внутренними 4 - и 5 -оболочками, которые заэкранированы от влияния кристаллического поля внешними электронами.

Поэтому для ионов группы железа в формуле (11.21) надо

заменить на , а множитель Ланде на 2. Ферромагнетизм. Феноменологическая теория ферромагне-

тизма была построена задолго до создания квантовой механики в 1907 г. французским физиком П. Вейссом (1865–1940). Для описания взаимодействия электронов он предположил, что в фер-

ромагнетике имеется некоторое эффективное магнитное полеэф (это поле называют также обменным, оно имеет чисто квантовомеханическую природу). Величина обменного поля пропорциональна имеющейся намагниченности (количеству электронов с коррелированными направлениями магнитных моментов)

где — некоторая константа, положительная у ферро- и отрицательная у антиферромагнетиков (в антиферромагнетиках спины магнитных моментов соседних атомов в решетки антипараллельны).

Мы уже упоминали, что выше температуры Кюри C ферромагнетик является парамагнетиком — тепловое движение полно-

стью разупорядочивает магнитные моменты атомов. Чтобы описать температурное поведение восприимчивости ферромагнетика в парамагнитной фазе, мы можем воспользоваться формулой (11.21), но надо, естественно, учесть, что имеется дополнительное поле эф. С учетом поля эф эту формулу следует записать в виде

и носит название «формула Кюри–Вейсса». Закон Кюри–Вейсса получен при довольно искусственном предположении о наличии дополнительного поля эф. В отличие от квантовомеханического подхода эта теория имеет, конечно, приближенный характер и формула Кюри–Вейсса не имеет всеобщей применимости. Она правильно указывает на наличие особой точки , когда вещество переходит из ферромагнитного состояния в парамагнитное . Магнитные свойства вещества в ферромагнитном состоянии она не описывает совсем, но температурную зависимость магнитной восприимчивости ферромагнетиков, находящихся в парамагнитном состоянии, описывает, как оказывается, неплохо.

При стремлении температуры к , называемой парамагнитной точкой Кюри, восприимчивость неограниченно возрастает из-за того, что тепловое движение все меньше препятствует магнитным моментам атомов ориентироваться в одном направлении. Напомним, что у парамагнитных веществ, в соответствии

иметь в виду, что точка Кюри C определяется как температура фазового перехода из парамагнитного в ферромагнитное состояние, т. е. это температура, ниже которой в образце устанавливается дальний магнитный порядок. В уравнении Кюри–Вейсса является фактически параметром и, как правило, C .

11.3. Квантовомеханическое описание ферромагнетизма

В классической физике все магнитные свойства микро- и макросистем определяются только магнитными взаимодействиями микрочастиц. В то же время температура Кюри C многих

ферромагнетиков порядка 102–103 К и, следовательно, соответствующие этим температурам энергии Б 10 7–10 6 Дж (от 0,01 до 0,1 эВ), что в десятки или сотни раз больше любой возможной энергии чисто магнитной связи. Кроме того, опыты в 1927 г. советского физика Я.Г. Дорфмана (1898–1974) по определению отклонения -частиц в спонтанно намагниченном ферромагнетике показали однозначно, что внутри ферромагнетика нет никакого эффективного поля магнитного происхождения. Следует упомянуть в связи с этим и результаты опытов Эйнштейна и де Гааза в 1915 г., в которых была впервые обнаружена связь между магнитным и механическим моментами. Из этих опытов, как было потом показано в точных количественных экспериментах, следовало, что отношение магнитного момента к механическому для ферромагнитного образца равно

Это отношение вдвое больше ожидавшейся величины для орбитального движения электрона, и тем самым опыт Эйнштейна–де Гааза показывает, что магнетизм связан не с пространственным движением электрона, а с его спином.

Эти факты позволяют предположить, что такое яркое магнитное явление, как ферромагнетизм, по своему происхождению

восновном не является магнитным эффектом, а обусловлено электрическими силами связи атомных носителей магнетизма

втвердом теле. В гл. 9 раздела IV на примере молекулы водорода было показано, что энергия существенным образом зависит от ее магнитного состояния и определяется знаком обменного взаимодействия. Естественно предположить, что именно обменное взаимодействие ответственно и за возникновение спонтанной намагниченности ферромагнетика. Эта идея была внесена в теорию ферромагнетизма впервые в 1928 г. независимо В. Гейзенбергом и Я.И. Френкелем.

Простейшая модель ферромагнетизма основывается на представлении, что вся обусловленная принципом Паули зависимость энергии от намагниченности проявляется посредством энергии обмена, и фактически она является непосредственным обобщением теории молекулы водорода на случай большого числа атомов. Иными словами, предполагается, что имеется система (кристалл), состоящая из водородоподобных атомов, электроны которых находятся в -состоянии. Обменная энергия кристалла есть сумма обменных энергий между соседними атомами и записывается следующим образом:

В этом выражении — это скалярное произведение векторов-го и -го спина (энергия взаимодействия записана в виде, аналогичном взаимодействию двух магнитных диполей), а штрих у знака суммы означает, что при суммировании, чтобы не учитывать каждую пару дважды, надо считать, что . Так как в квантовой механике проекции спина на заданную ось могут принимать лишь дискретные значения, то и скалярное произведение в формуле (11.26) принимает лишь дискретные значения.

Применим, в качестве примера, написанное выражение для

если обменный интеграл отрицателен для рассматриваемой

Разность энергий синглетного и триплетного состояний равна

2 2 , и, в соответствие с полученным ранее результатом, синглетное состояние молекулы водорода действительно обладает более низкой энергией.

Итак, если обменный интеграл положителен, то низшую энергию имеет симметричное состояние и простейшим примером является ферромагнитное состояние, а если он отрицателен, то низшую энергию имеет антисимметричное состояние и этот случай соответствует антиферромагнитному состоянию с антипараллельными спинами.

В заключение следует сделать несколько замечаний. Первоначальная теория Гейзенберга—Френкеля выявила квантовую

первопричину магнитного упорядочения и из нее следуют два важнейших принципиальных вывода:

1.если обменный интеграл положителен, то может возникнуть состояние самопроизвольной намагниченности — ферромагнетизм;

2.величина энергии обменного взаимодействия достаточна для возникновения ферромагнетиков с температурой Кюри по-

рядка 103 K.

Правильная в своей основе, эта теория позволила понять целый ряд опытных данных. Энергия взаимодействия электронов между собой (перекрытие электронных оболочек), как энергия взаимодействия одноименных зарядов, положительна, а энергия взаимодействия электронов и ядер — отрицательна. Поэтому благоприятствовать положительному значению будет увеличение отношения расстояния между ионами в кристалле к радиусу электронной оболочки , хотя при этом абсолютное значение должно уменьшаться. Грубо говоря, атомы ферромагнитного вещества должны находиться достаточно далеко друг от друга, и эти условия действительно соблюдаются на опыте. Все ферромагнитные элементы принадлежат к числу переходных элементов, а ферромагнитные сплавы и соединения обязательно содержат в себе переходные элементы. Именно у переходных элементов имеется незаполненная электронная -оболочка, т. е.

электронная оболочка с большим орбитальным числом и не равным нулю суммарным спиновым моментом.

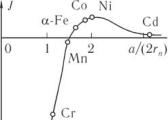
На рис. 11.4 показана вычисленная Бете зависимость обменной энергии от отношения постоянной решетки к диаметру незаполненной оболочки 2 , которая качественно правильно отражает зависимость обменного интеграла от расстояния.

Ферромагнитные элементы Fe, Co, Ni имеют наибольшее значение обменного интеграла, у гадолиния и некоторых других редкоземельных элементов уже очень велико, поэтому обменный интеграл у них хотя и положителен, но мал, и точки Кюри низкие.

На основании такой схемы удается «объяснить» не только ферромагнетизм Fe, Co, Ni, но и антиферромагнетизм Mn и Cr, ферромагнетизм так называемых гейслеровых сплавов, зависимость температуры Кюри от давления и т. д.

Например, в марганце расстояние между атомами ( 21,5) маленькое, оно близко к расстоянию, при котором меняет-

ся знак объемного интеграла. Небольшое увеличение постоянной решетки марганца должно превратить его из антиферромагне-

тика в ферромагнетик. Действительно, добавление к марганцу небольших добавок азота, увеличивающих постоянную решетки, приводит к появлению ферромагнетизма. Это же относится и к сплаву Гейслера Cu2MnAl, который состоит из неферромагнитных металлов, но является ферромагнетиком. Внедрение дополнительных компонентов «раздувает» решетку, и ионы марганца упорядочиваются ферромагнитно.

И, тем не менее, все эти примеры скорее удивительны. Давайте внимательнее рассмотрим ситуацию с прямым обменом. Нас интересует взаимодействие между спинами электронов различных ионов, как это имеет место в молекуле водорода. Но

вмолекуле водорода связанному состоянию соответствует антипараллельная ориентация спинов. Поэтому трудно объяснить тот факт, что многие элементы ферромагнитны. Скорей всего они должны быть антиферромагнетиками. Мы можем понять, почему-электроны каждого отдельного иона стремятся расположиться так, чтобы полный спин, скажем, в случае Fe был равен 5/2, но мы не можем понять, почему взаимодействие магнитных моментов соседних ионов приводит к параллельной их ориентации.

Все дело в том, что для таких металлов ситуация намного сложнее. В них имеются обычные -электроны, образующие зону проводимости и способные взаимодействовать с -электро- нами. Взаимодействуя обменным образом, -состояния различных атомов также должны перекрываться, образуя зону, т. е.-электроны, строго говоря, не локализованы. Существует общая теория ферромагнетизма, основанная на этой идее — модель коллективизированных электронов Э. Стонера, которая также описывает многие черты ферромагнитных веществ. Какая из моделей более подходит для объяснения ферромагнетизма металлов — модель локализованных электронов или модель коллективизированных электронов, пока не ясно. И тот, и другой механизм упорядочения электронных спинов вносит свой вклад.

Итак, во многих веществах появляется возможность непрямого обмена между удаленными магнитными ионами, когда почти нет перекрытия их волновых функций и связь осуществляется промежуточными агентами — в диэлектриках и полупроводниках это косвенное обменное взаимодействие через немагнитный ион-лиганд, находящийся между двумя магнитными ионами, а

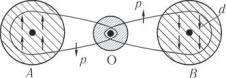
вметаллических системах связь осуществляется электронами проводимости. Типичным примером является антиферромагнитное соединение MnO, упорядочение которого происходит за счет косвенного обмена, когда -электроны иона Mn связаны с электронами кислорода, а те в свою очередь взаимодействуют через обмен с -электронами второго иона марганца, как это показано на рис. 11.5. Если атом имеет спин « », то он может принять электрон со спином « » из -состояния атома кислорода; если

атом имеет спин « », то он может забрать оставшийся электрон атома кислорода. Таким образом, взаимодействие между спинами -электронов атома кислорода преобразуется во взаимодействие между спинами -оболочек магнитных

ионов.

Подытоживая сказанное, видно, что во всех случаях появления ферромагнетизма

у элементов и соединений он связан с переходными элементами и, таким образом, первоначальная модель Гейзенберга–Френ- келя, в которой, как предполагалось, электроны находятся в -состоянии, представляет собой довольно грубое приближение к действительности, но основная идея обменного взаимодействия правильна. Прямые расчеты по этой модели показывают, что не только значительно меньше по абсолютной величине, чем требуется, но во многих конкретных случаях имеет отрицательный знак. Просто модель прямого обмена слишком груба, чтобы от нее можно было требовать количественного сравнения с опытом, и в современных расчетах всегда учитывается как возможность косвенного обмена, так и более сложных магнитных взаимодействий.

Конечно, сейчас понятно, что модель Гейзенберга–Френкеля представляет собой довольно грубое приближение к действительности, но основная идея о квантовомеханической природе магнетизма, вытекающей из принципа Паули и роли обменного взаимодействия, которое может сделать намагниченное состояние более выгодным, правильна. Она сыграла и играет существенную роль в развитии учения о магнетизме веществ.

С точки зрения термодинамики переход вещества из парамагнитного в ферромагнитное состояние есть фазовый переход II рода. Для фазовых переходов II рода характерно появление по одну сторону от точки перехода некоторой физической величины, которая равна нулю по другую сторону от точки перехода. При этом плотность меняется непрерывно, теплота не выделяется и не поглощается.

В парамагнитном состоянии магнитные моменты (спины) отдельных атомов ориентированы случайно, и поэтому суммарный магнитный момент кристалла равен нулю. В отличие от этого в ферромагнитном состоянии спины отдельных атомов частично или полностью упорядочены — выстроены вдоль некоторого общего направления. В результате магнитный момент ферромагнетика оказывается отличным от нуля. Переход от парамагнитного к ферромагнитному состоянию происходит при температуре Кюри. Величина суммарного магнитного момента убывает с воз-