студ ивт 22 материалы к курсу физики / belonuchkin_ve_zaikin_da_tsipeniuk_ium_kurs_obshchei_fiziki

10.5 ] Энергия границы между фазами 541

с принципом неопределенностей он порядка . Следовательно, кинетическая энергия пары порядка

Мы видим, что в среднем каждый сверхпроводящий электрон вносит в энергию конденсации лишь Ф часть от энергии щели. Можно сказать, что обычное фермиевское распределение для сверхпроводящих электронов при 0 искажается лишь в слое с относительной толщиной порядка Ф .

10.5. Энергия границы между фазами

При анализе поведения любой физической системы необходимо помнить, что все системы стремятся перейти в состояние с наименьшей энергией. В случае сверхпроводящих металлов существует взаимодействие электронов и решетки, которое делает энергию сверхпроводящего состояния более низкой, чем энергия нормального состояния, если температура достаточно низка. Поскольку система всегда стремится перейти в состояние с наименьшей энергией, металл становится сверхпроводящим при достижении некоторой температуры перехода. При дальнейшем понижении температуры разница между энергиями нормального и сверхпроводящего состояний увеличивается. Если при некоторой температуре ниже температуры перехода включить внешнее магнитное поле, то сверхпроводник вытолкнет это поле. На это требуется энергия, которую должен дать сам сверхпроводник. Энергия здесь выступает в форме кинетической энергии движения электронов, образующих, согласно эффекту Мейсснера, поверхностные токи. При увеличении силы поля энергия, требуемая сверхпроводнику для его выталкивания, также увеличивается, так что при критическом значении поля энергия сверхпроводящего состояния оказывается уже выше, чем соответствующая энергия нормального состояния. В этом случае сверхпроводник вынужден вернуться в нормальное состояние.

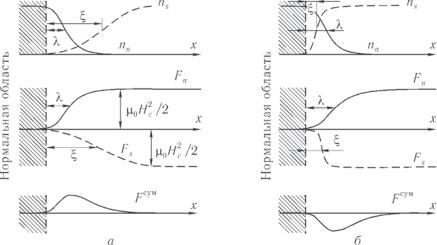
Рассмотрим сверхпроводящую область, прилегающую к нормальной. На границе не может быть резкого перехода от полностью нормального к полностью сверхпроводящему состоянию. Магнитный поток проникает на расстояние вглубь сверхпроводящей области, и в соответствии с концепцией когерентности, в сверхпроводящей области число сверхпроводящих электроновна единицу объема медленно повышается на расстоянии, примерно равном длине когерентности .

Теперь рассмотрим свободную энергию на границе. Если граница стабильна, то сверхпроводящие и нормальные электроны

на единицу объема должны быть одинаковы. Свободная энергия сверхпроводящей области меняется относительно свободной энергии нормальной области в результате двух обстоятельств. Благодаря наличию упорядоченных сверхпроводящих электронов плотность свободной энергии сверхпроводящего состояния понижается на величину , и, кроме того, поскольку сверхпроводящая область обладает намагниченностью, уничтожающей внутренний магнитный поток, существует положительный «магнитный» вклад в плотность ее свободной энер-

что внутри сверхпроводящей области оба вклада уничтожаются и плотность свободной энергии такая же, как в прилегающей нормальной области. Однако на самой границе степень упорядочения (т. е. число сверхпроводящих электронов) повышается постепенно на расстоянии, определяемом длиной когерентности, поэтому спад свободной энергии, связанный с увеличением упорядоченных электронов, происходит на том же расстоянии. С другой стороны, «магнитный» вклад в свободную энергию возрастает на расстоянии порядка глубины проникновения . Вообще говоря, не равно , так что оба вклада не обращаются в нуль вблизи границы. Если (как на рис. 10.12 a) длина когерентности больше глубины проникновения, полная плотность

Рис. 10.12

свободной энергии вблизи границы возрастает; это значит, что существует положительная поверхностная энергия (рис. 10.12 a внизу). Как легко видеть из рис. 10.12, значение этой поверх-

ницу площади поверхности. Это становится очевидным, если заменить две кривые на рис. 10.12 а прямоугольниками, в которых плотность магнитного потока и резко изменяются на расстояниях соответственно и от края нормальной области.

Именно такое соотношение между длиной когерентности и лондоновской длиной ( ) имеет место в сверхпроводниках I рода, которые мы до сих пор рассматривали. Однако если имеет место обратное соотношение между и , то поверхностная энергия будет отрицательна, как это показано в нижней части рис. 10.12 б, и в этом случае сверхпроводник будет принадлежать к сверхпроводникам II рода. К сверхпроводникам второго рода относятся сплавы обычных сверхпроводников (таких, как свинец, олово ртуть), очень тонкие сверхпроводящие пленки и сверхпроводники типа ниобия, которые имеют значительно более высокие температуры перехода, чем обычные сверхпроводники. К сверхпроводникам II рода относятся и высокотемпературные сверхпроводники.

В табл. 10.3 приведены значения лондоновской длины и длины когерентности для ряда сверхпроводников. Микроскопические параметры высокотемпературных сверхпроводников приведены в § 10.8 (см. табл. 10.4).

Таблица 10.3

Сверхпроводящие характеристики некоторых элементов и соединений

Следует иметь в виду, что практически любой сверхпроводник I рода можно превратить в сверхпроводник II рода введением примесей, дислокаций или каких-либо иных дефектов решетки. Если эти дефекты распределены однородно, так что в сверхпроводнике не образуется макроскопических участков

с различающимися свойствами, то вся роль дефектов сводится к нарушению пространственной корреляции электронов. Это же замечание относится и к сверхпроводникам II рода, сверхпроводящие характеристики которых сильно зависят от чистоты материала, степени и характера обработки.

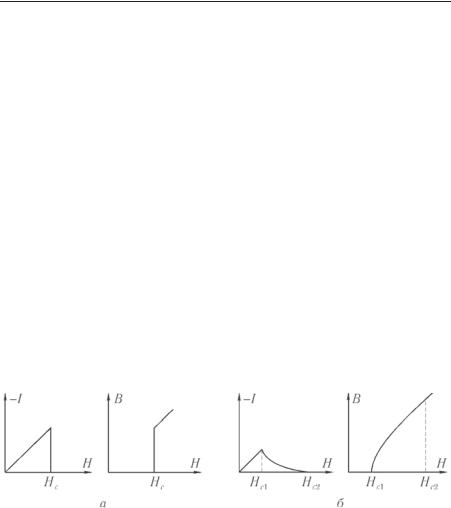
Отчетливо видно, что образование фазовой границы между нормальной и сверхпроводящей областями при сопровождается выигрышем энергии. Сверхпроводник, обладающий таким свойством, должен иметь минимум свободной энергии, когда в нем содержится максимальное количество межфазных границ.

Иными словами, конфигурация нормальных областей, проходящих через сверхпроводящий материал, должна быть такой, чтобы отношение поверхности нормального материала к его объему было максимально. В этом случае получается совершенно новое, так называемое смешанное состояние, характерное для сверхпроводников II рода.

10.6. Вихревая структура сверхпроводников II рода

Явление частичного проникновения магнитного потока в сверхпроводник было обнаружено Л. В. Шубниковым в 1937 г. Теперь нам понятно, почему возможно такое поведение сверхпроводника в магнитном поле: сверхпроводнику с отрицательной поверхностной энергией выгодно в определенном интервале полей перейти в смешанное состояние — частично «пропуская» через себя магнитный поток, сверхпроводник проигрывает в энергии конденсации, но больше выигрывает в уменьшении энергии, необходимой для выталкивания поля из объема, и тем самым сверхпроводящее состояние может существовать при более высоких значениях магнитных полей.

Поскольку любое отличное от нуля магнитное поле обусловливает протекание в сверхпроводнике незатухающего сверхпроводящего тока, то в смешанном состоянии токи текут и в толще сверхпроводника. Разумеется, эти токи должны быть замкнутыми, так как только тогда состояние будет стационарным.

В 1952 г. А.А. Абрикосов показал, что в сверхпроводниках II рода наблюдается качественно отличная от сверхпроводников I рода картина разрушения сверхпроводника полем. Им было показано, что в присутствие сильного магнитного поля состоянием с наименьшей энергией является состояние с электронными вихрями. Согласно теории Абрикосова вихрь в самом простом случае представляет собой цилиндрическую трубку нормального металла очень малого радиуса (порядка одной стотысячной сантиметра), через которую магнитный поток может проникать внутрь сверхпроводника. Магнитное поле поддерживается в вихре электрическими токами, которые текут вокруг

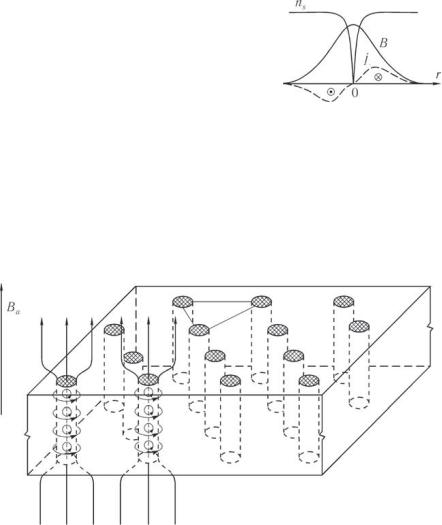
548 Сверхпроводимость [ Гл. 10

10.8. Высокотемпературные сверхпроводники

Как указывалось в начале этой главы, в настоящее время к высокотемпературным сверхпроводникам (ВТСП) относятся соединения, основанные на оксидах меди и имеющие температуру сверхпроводящего перехода в области азотных температур. Сейчас известно более двух десятков ВТСП соединений, которые являются купратами различных металлов, и они по названию основного металла соответственно называются иттриевыми ВТСП (например, YBa2Cu3O7 , 90 K), висмутовыми (Bi2Sr2CaCu2O8, 95 K), таллиевыми (Tl2Ba2CaCu2O8,110 K), ртутными (HgBa2CaCu2O6, 125 K).

Высокотемпературные сверхпроводники являются типичными представителями сверхпроводников II рода с очень большим отношением лондоновской длины к длине когерентности — порядка нескольких сотен. Поэтому второе критическое магнитное поле2 имеет очень высокое значение, в частности у Bi 2212 (так для краткости указывают ВТСП-материалы; цифры обозначают стехиометрические индексы составляющих их компонентов) оно составляет примерно 400 Тл, а 1 равно нескольким сотням эрстед (1 э 10 4 Тл). В табл. 10.4 приведены параметры некоторых типичных представителей купратных семейств.

Таблица 10.4

Параметры ВТСП-материалов

В монокристаллах высокотемпературных сверхпроводников в магнитных полях больших 1 наблюдается регулярная вихревая структура, подобная ранее обнаруженной в традиционных сверхпроводниках II рода.

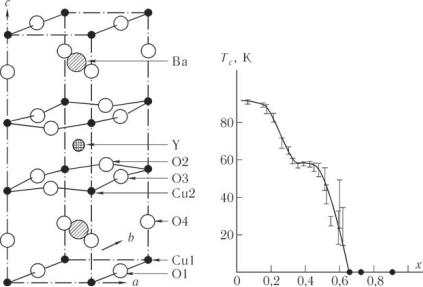
В состав оксидных сверхпроводников входит обычно 4–5 различных сортов атомов, а в элементарную кристаллографическую ячейку до 20 атомов. Практически все ВТСП обладают слоистой структурой типа перовскита с плоскостями из атомов Cu и O. На рис. 10.17 показана кристаллографическая структура типичного широко распространенного высокотемпературного сверхпроводника — иттриевого соединения YBa2Cu3O7 ; стрелкой показано положение проводящих плоскостей Cu—O.

Существенную роль в сверхпроводимости играет наличие кислорода. Атомы кислорода могут занимать две различные позиции: в плоскостях CuO2 (эти позиции сейчас обозначаются как O3) и в цепочках CuO (O1) (рис. 10.17). Химическая связь атомов кислорода в цепочках невелика и при термической обработке они могут выходить из кристалла, а в цепочках образуются вакансии (дырки), что сопровождается структурными превращениями. Так полному заполнению кислородом медных цепочек в иттриевом купрате ( 7) соответствует орторомбическая структура, а в случае отсутствия атомов O1 решетка имеет тетрагональную структуру ( 6). На рис. 10.18 показана

зависимость от содержания кислорода в иттриевых купратах YBa2Cu3O7 .

Результаты многочисленных экспериментов подтверждают предположение, что плоскости с кислородом являются основным объектом в кристаллографической решетке, которые ответственны как за проводимость этих оксидных соединений, так и за возникновение в них сверхпроводимости при высоких температурах.

Мы рассматривали выше физические свойства монокристаллических ВТСП. Исторически первые ВТСП были получены спеканием соответствующих химических компонентов с последующим отжигом в атмосфере кислорода. В результате получается керамический сплав, состоящий из спекшихся сверхпроводящих гранул. Поэтому такие ВТСП называют керамическими или гранулярными. Характерный размер гранул обычно составля-

ет около 10 мкм. Первые эксперименты проводились именно на таких керамических образцах, и лишь потом научились выращивать монокристаллические образцы, что до сих пор является довольно трудной технологической задачей. Следует отметить, что гранулярные сверхпроводники обладают новыми интересными физическими свойствами, в принципе невозможными в классических негранулярных низкотемпературных сверхпроводниках. Практически все прикладные исследования, о которых пойдет речь в следующем параграфе, проводятся именно на основе керамических образцов.

10.9. Применения сверхпроводимости

Вопросы различных применений сверхпроводимости стали обсуждаться практически сразу же после открытия этого поразительного явления. Еще Камерлинг-Оннес считал, что с помощью сверхпроводников можно экономичным образом создавать сильные магнитные поля. Однако реально использование сверхпроводимости началось лишь в конце 50-х — начале 60-х гг. XX века. В настоящее время уже работают сверхпроводящие магниты практически любых размеров и любой формы. Они вышли за рамки чисто научных исследований, и сегодня их широко используют в лабораторной практике, в ускорительной технике, медицинских томографах, установках для управляемой термоядерной реакции. С помощью сверхпроводимости стало возможным намного повысить чувствительность многих видов измерений. Сверхпроводимость стала не только технической дисциплиной, но и отдельной отраслью промышленности. И, конечно, открытие высокотемпературной сверхпроводимости создало предпосылки к более широкому внедрению в повседневную практику различных сверхпроводящих устройств. Ниже мы приведем для иллюстрации лишь несколько примеров.

Наибольшее применение сверхпроводники нашли в настоящее время в области создания сильных магнитных полей. Современная промышленность производит из сверхпроводников II рода разнообразные провода и кабели, используемые для изготовления обмоток магнитов. Преимущества сверхпроводящих магнитов достаточно очевидны. Не говоря даже о возможности получения с помощью сверхпроводников значительно более сильных магнитных полей (сейчас в чисто сверхпроводящих системах достигнуты поля более 20 Тл), чем при использовании железных магнитов, сверхпроводящие магниты являются и более экономичными. Так, например, для поддержания в медном соленоиде с внутренним диаметром 4 см и длиной 10 см поля в 10 Тл необходима электрическая мощность не менее 5100 кВт,