студ ивт 22 материалы к курсу физики / belonuchkin_ve_zaikin_da_tsipeniuk_ium_kurs_obshchei_fiziki

9.5 ] Электроны в полупроводниках 501

другой электрон этой зоны. В результате вакансия переместится в направлении, противоположном перемещению этого электрона, и движение такого «пустого места» будет эквивалентно движению положительного заряда.

Так положительно заряженное атомное состояние передвигается по кристаллу— именно состояние, а не сам положительно заряженный ион. Положительно заряженное состояние, как уже упоминалось в § 9.3, называется дыркой. Дырка ведет себя подобно положительно заряженному электрону; это новая квазичастица в кристалле, она характеризуется своей эффективной массой. Ясно, что введение дырок и соответственно дырочной проводимости не означает их реального существования. Такое представление — удобный способ описания электронной системы, которая при определенных условиях под влиянием поля кристаллической решетки столь кардинально меняет свое поведение, что оно становится аналогичным по характеру своего движения

поведению системы положительно заряженных частиц — дырок.

Уровень Ферми в полупроводниках. Рассмотрим вопрос о положении уровня Ферми в полупроводниках. Как мы увидим дальше, уровень Ферми в полупроводниках не имеет такого простого физического смысла, как в металлах, он зависит от температуры, и поэтому фактически не является параметром вещества. Поэтому более правильно говорить о значении химического потенциала.

Прежде всего мы покажем, что в чистом (беспримесном) полупроводнике уровень Ферми расположен посредине запрещенной зоны. Следует отметить, что ширина запрещенной зоны в полупроводниках значительно больше характерной тепловой энергии Б при обычных температурах, что приводит к следующим закономерностям. Формула (9.20), описывающая распределение Ферми, показывает, сколько электронов (в среднем) находится в каждом состоянии и в соот-

водимости и на расстоянии от дна запрещенной зоны, так что

(рис. 9.11). За нуль энергии примем положение дна зоны проводимости.

водимости. Для этого надо с учетом плотности состояний проинтегрировать функцию распределения электронов по всем возможным энергетическим состояниям электрона в зоне проводимости :

где — элемент фазового пространства. Кроме того, мы учли, что величина , отсчитываемая от дна зоны проводимости, отрицательна. Еще раз подчеркнем, что в этой формуле распределение Ферми заменено больцмановским распределением электронов по энергиям. Экспоненциальный множитель в выражении под интегралом определяет вероятность возбуждения электрона с энергией , отсчитываемой от уровня Ферми.

Интегрирование мы распространили до бесконечности в силу

определяет эффективное число уровней в зоне проводимости и носит название статистического фактора зоны.

9.5 ] Электроны в полупроводниках 503

Аналогичные вычисления можно провести и для концентрации дырок:

В полупроводнике без примесей носители электричества (элек-

Как правило, эффективные массы электронов и дырок не сильно

а значит и уровень Ферми в собственных полупроводниках расположен практически посредине запрещенной зоны.

Из формул (9.52) и (9.55) следует, что произведение концентраций электронов и дырок равно

где сумма заменена на — ширину запрещенной зоны. Проводимость, обусловленную процессом теплового возбуждения исходной (без примесей) кристаллической решетки, называют собственной, поскольку она определяется свойствами самого кристалла. Соответственно и концентрацию носителейв зоне проводимости, возникающих за счет переходов из валентной зоны, называют концентрацией собственных носителей. В беспримесном полупроводнике, как следует из выражения (9.57), концентрация собственных носителей , равная как концентрации электронов, так и дырок, которые рождаются

парами, может быть записана в виде

Полученное выражение примечательно тем, что оно не зависит от числа и вида примесей, о которых пойдет речь ниже, так как при его выводе мы предполагали, что уровень Ферми расположен

произвольно в запрещенной зоне.

Роль примесей. Перейдем к рассмотрению вопроса о примесях в полупроводниках. Некоторые примеси (как и некоторые виды дефектов) могут очень сильно влиять на электрические свойства полупроводников. Например, добавление бора в крем-

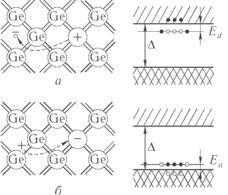
ний в количестве 10 5 атомных частей увеличивает проводимость чистого кремния в 1000 раз (при комнатной температуре). Полупроводники с примесями называются примесными. Рассмотрим влияние примесей на физические свойства широко распространенных полупроводниковых материалов Ge и Si, которые образуют решетку типа алмаза. В такой структуре каждый атом обладает 4-мя ковалентными связями, так что у каждого атома 4 ближайших соседа. Если добавить примесный атом с валентностью 5 (P, As, Sb), то один валентный электрон оказывается «лишним», он теряется и атом As становится положительно заряженным. Такие примеси (в данном случае элементов 5-й группы) называются донорными атомами, а полупроводники с такими примесями полупроводниками -типа. Схематически это иллюстрируется на рис. 9.12 а, на котором через обозначена ширина

запрещенной зоны, — положение донорного уровня. Если же ввести 3-х валентные атомы (B, Al, Ga, In), то, наоборот, одна связь оказывается «пустой», образуется «дырка», которая легко может заполниться электроном (рис. 9.12 б, — положение акцепторного уровня). Такие атомы называются акцепторными, соответственно полупроводники с акцептор-

Рис. 9.12 ными примесями называются

полупроводниками -типа. Избыточный электрон донорного атома движется в создаваемом примесным атомом кулоновском поле с потенциалом

0 , где — диэлектрическая проницаемость полупроводника. Учитывать влияние среды на потенциал взаимодействия через диэлектрическую проницаемость (макроскопически среднюю величину) можно только в том случае, если орбита электрона столь велика, что она много больше расстояния между атомами. Как следует из приведенных ниже оценок, такая ситуация действительно имеет место.

Нам интересно оценить энергию возникающего уровня, т. е. вычислить энергию связи электрона с примесным атомом-до- нором. Если те предположения, о которых говорилось выше, справедливы, то можно рассматривать просто примесный атом как изолированный и использовать боровскую теорию водородоподобного атома, заменив на и учитывая диэлектрическую проницаемость среды. Для энергии связи электрона и радиуса

9.5 ] Электроны в полупроводниках 505

первой орбиты в боровском атоме заряда мы имеем следующие соотношения:

проницаемость 16. Избыточный электрон донорного атома

Итак, мы видим, что действительно, радиус первой орбиты много больше межатомного расстояния, а энергия связи много меньше ширины запрещенной зоны (щели), т. е. донорный уровень расположен очень близко к дну зоны проводимости. Совершенно аналогично, акцепторный уровень располагается вблизи дна запрещенной зоны.

Столь большой радиус электронной орбиты в примесных атомах приводит к тому, что электронные орбиты перекрываются даже при относительно низких концентрациях примесей. Если к тому же учесть, что энергия связи примесного электрона намного меньше, чем внешних электронов основных атомов решетки, то оказывается, что вероятность делокализации примесных электронов вполне реальна. Действительно, проницаемость потенциального барьера, разделяющего атомы определяется ве-

личиной 2 2 (см. (9.22)). Величина

есть не что иное, как энергия связи электрона. Для электронов

Æ

основных атомов 10 эВ, а 1 А, т. е. произведение

Æ

3 эВ А. Для примесных атомов такого же порядка величина получается при их концентрации порядка 1017 см 3 (мы для простоты оценки считали, что эффективные массы электронов одинаковы). Таким образом, электроны донорных атомов образуют свою очень узкую зону проводимости (их число намного меньше основных), как это схематически показано на рис. 9.12 справа.

Обратимся теперь к вопросу о том, где расположен уровень Ферми в примесных полупроводниках. Рассмотрим полупроводник -типа. Как было выше показано, донорный уровень располагается вблизи дна зоны проводимости. Поэтому электроны в зону проводимости попадают преимущественно за счет переходов с примесного уровня, и это означает, что фактически такой полупроводник будет при не слишком высоких температурах

вести себя так, как будто ширина его запрещенной зоны равна энергии донорного уровня , отсчитываемой от дна зоны проводимости. Таким образом ясно, что уровень Ферми при 0 будет равен 2. Понятна также и температурная зависимость энергии Ферми — по мере истощения носителей, имеющихся на примесном уровне, все большую роль будет играть собственная проводимость полупроводника, определяемая переходами электронов из валентной зоны в зону проводимости, и уровень Ферми

врезультате опустится до значения 2, как это имеет место

вбеспримесном полупроводнике. Аналогично у полупроводника-типа уровень Ферми при нулевой температуре равен 2 и по мере увеличения температуры он будет увеличиваться до 2.

Обсудим вопрос о том, каков закон распределения по энергиям электронов, попадающих в зону проводимости с донорных

уровней. При низких концентрациях ( 1014–1017 см 3) примесные состояния находятся в запрещенной зоне, их энергия составляет примерно 0,01 эВ, и, как уже указывалось, так как энергия теплового движения при комнатных температурах равна 0,025 эВ, практически все атомы донорных примесей отдают свои электроны в зону проводимости. При этом точно так же, как и для чистого полупроводника, распределение электронов в зоне проводимости по энергии является больцмановским, но по другой причине. Донорные атомы «поставляют» в зону проводимости не более 1017 частиц в 1 см3, что соответствует для электронов с эффективной массой 0,03 0,05 температуре вырождения 0 250 K. Поэтому при обычных температурах фермиевское распределение с резкой границей становится больцмановским распределением.

На основе приведенных выше соображений легко качественно получить температурную зависимость концентрации электронов и дырок в примесных полупроводниках (для определенности будем рассматривать полупро-

Если температура такова, что Б , но Б , то все доноры ионизованы и , где — концентрация донорных атомов. При условии Б концентрация носителей практиче-

ски равна концентрации собственных носителей и определяется шириной запрещенной зоны.

Качественно температурный ход концентрации носителей, что практически эквивалентно температурной зависимости электропроводности, изображен на рис. 9.13.

9.6. Контактные явления в полупроводниках

Рассмотрим, что происходит при контакте металла с полупроводником с донорными примесями, т. е. с полупроводником-типа. Пусть металл M, имеющий работу выхода М , приведен в контакт с полупроводником П, имеющим работу выхода П . У полупроводника различают две работы выхода: термодинамическую П , равную расстоянию от уровня Ферми П до нулевого уровня П , и внешнюю 0, равную расстоянию от дна зоны проводимости до нулевого уровня (рис. 9.14 а). Процессы установления равновесия между проводниками определяются термодинамическими работами выхода, и поэтому под П мы будем подразумевать именно эту работу выхода.

Рис. 9.14

Если М П , то электроны будут перетекать из полупроводника в металл до тех пор, пока уровни их энергий Ферми не выровняются ( П М ) и не установится равновесие. Необходимость выравнивания энергий Ферми достаточно очевидна — если существует разность в положении уровней Ферми, то электроны будут для достижения минимума энергии в системе перетекать с более высокого уровня на более низкий энергети-

сторонах перехода имеют однородную плотность и распространяются на глубину 2 в - и -областях. Распределение зарядов показано на рис. 9.15 в. В соответствующих областях плотность заряда равна и . Электростатический потенциал определяется из решения одномерного уравнения Пуассона

где — диэлектрическая проницаемость материала. Граничные условия состоят в том, что функции и должны обращаться в нуль при 2. Решения этих уравнений, удовлетворяющие граничным условиям, суть

Соответствующая этим решениям кривая, иллюстрирующая рас-

где к — контактная разность потенциалов. Этот скачок потенциала равен работе, которую нужно совершить, чтобы перенести электрон из зоны проводимости -области в зону проводимости-области. Аналогичную работу нужно совершить, чтобы перенести через переход дырку. Отметим, что вольтметр, подключенный к – -переходу, показывает не величину контактной разности потенциалов, а разность уровней химического потенциала, т. е. в равновесии (без внешнего источника) его показания равны нулю.

Из выражения (9.67) также следует, каким образом зависит толщина запорного слоя от высоты потенциального барьера к и от концентрации донорной и акцепторной примесей :

Как указывалось выше, тепловое равновесие, устанавливающееся между двумя сторонами – -перехода, является дина-

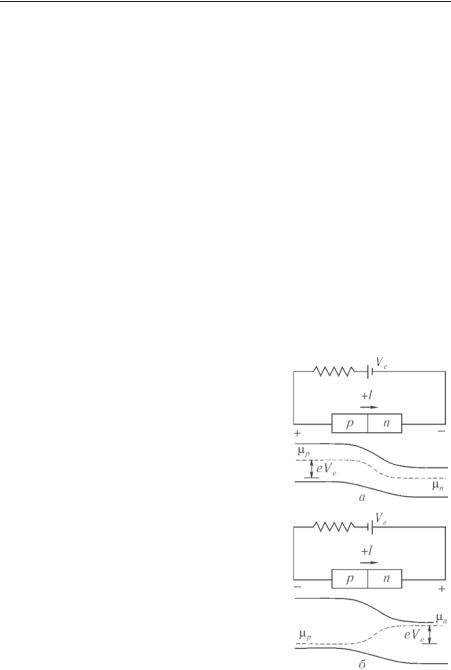
510 Электроны в кристаллах [ Гл. 9

мическим, т. е. оно характеризуется потоком носителей, которые показаны на рис. 9.16. Обозначим электронный ток, текущий направо, через , а текущий

налево — через .

В -области электроны попадают в зону проводимости с акцепторного уровня, а для этого им надо приобрести энергию возбуждения . Попав в зону проводимости, электроны свободно могут продиффундировать в -область и поэтому ток электронов пропорционален только их числу, т. е. пропорцио-

вероятность появления электронов в зоне проводимости пропорциональна Ф Б , но их диффузия в -область связана с преодолением потенциального барьера высотой

Ф . Ток пропорционален произведению этих двух больцмановских множителей, т. е. величине

Б , как и . Таким образом, движение электронов не вызывает результирующего тока. Аналогичным образом можно показать, что движение дырок также не создает тока.

Рассмотрим теперь неравновесную ситуацию, возникающую, когда на переход подается внешнее напряжение(напряжение смещения). Отсутствие равновесия связано с тем, что подключение внешней батареи приводит к появлению разности уровней химических потенциалов электронов и дырок . В силу того, что переходный слой обеднен носителями, он имеет очень большое сопротивление и практически все внешнее напряжение оказывается приложенным к области перехода, как это показано на рис. 9.17.

Если внешняя батарея подключена положительным полюсом к -области (так называемое обратное смещение, показанное на рис. 9.17 а), то края зон еще больше раздвигаются на величи-

ну к . При этом ток

, обусловленный неосновными носителями (электронами в -области и дырками в -области) не меняется, а ток основных