студ ивт 22 материалы к курсу физики / belonuchkin_ve_zaikin_da_tsipeniuk_ium_kurs_obshchei_fiziki

осталось вместо нее в нижнем, теперь уже не совсем полном сосуде? Пузырек, пустое место, дырка. На квантовом языке дырка — это состояние, освобожденное перешедшим на более высокий уровень электроном. Поведение такого образования во многом очень похоже на поведение настоящей частицы с собственным электрическим зарядом, противоположным электрону, и даже с собственной массой.

Итак, мы показали, что на спектр энергетических состояний электронов в кристалле существенным образом влияет взаимодействие электронов соседних атомов, образующих периодическую структуру. Влияние решетки рассмотрим для простоты на примере одномерной бесконечной цепочки, составленной из одинаковых атомов с одинаковым расстоянием между ними, причем реальную периодическую «цепочку» потенциальных ям ионов заменим «цепочкой» прямоугольных потенциальных ям, расположенных друг от друга на таком же расстоянии , как и ионы в кристалле. Когда атомы далеко друг от друга, волновые функции их валентных электронов точно такие же, как у изолированных атомов. Обозначим эти волновые функции через (например, для натрия это электрон в 3 -состоянии). По мере сближения атомов мы можем ожидать, что на каком-то расстоянии электрон с одного атома может перескочить на соседний. Если считать, что и в этом случае атомы все еще не очень близко расположены друг к другу, то такое движение электронов можно рассматривать как перескок электрона из состояния на такое же состояние соседнего атома 1 либо 1. Такое описание предполагает, что мы можем с хорошей точностью волновую функцию электрона записать в виде линейной комбинации состояний атомов цепочки, т. е.

Если считать, что электрон достаточно сильно локализован, то существен лишь его перескок в соседние потенциальные ямы, и фактически в сумме (9.26) останутся лишь три члена, что значительно облегчает решение поставленной задачи. Обсуждаемая нами модель называется моделью сильной связи.

В результате математических выкладок мы получаем, что при этих предположениях электрон может иметь следующие значения энергии:

где — константа, характеризующая вероятность перескока электрона на соседний атом и тем самым ширину зоны, а 0 — энергия электрона в свободном атоме, «не искаженная» наличием

соседей в кристалле. Мы получили, что при любом выборе имеется решение с определенной энергией, но, в отличие от дискретных уровней атома, в кристалле возможна целая полоса (зона) разрешенных значений, и ширина этой зоны зависит от степени перекрытия волновых функций валентных электронов соседних атомов (степени делокализации электрона).

Полученный результат легко обобщается на случай трехмерной решетки и, скажем, при учете перескока электронов только к ближайшим соседним ионам закон дисперсии будет иметь вид

0 2 2 2 (9.28)

В области малых значений (область длинных волн, электронов малой энергии) закон дисперсии остается квадратичным, как это следует из модели свободных электронов. Такие электроны «не чувствуют» кристаллическую решетку. Действительно, если предположить, что , то при 1 мы имеем

В одномерном случае закон дисперсии для электронов в зоне проводимости приобретает вид

Конечно, в рассмотренной модели сильной связи влияние решетки предельно упрощено, но она качественно правильно передает основные черты поведения коллективизированных электронов (электронов проводимости) в кристалле.

9.3. Динамика электронов в кристаллической решетке

Как видно из проведенного нами анализа возможных энергетических состояний электронов, по мере увеличения волнового вектора закон дисперсии изменяется и это приводит к существенному изменению динамики электронов в решетке. Изменение динамики движения электрона проявляется в том, как он реагирует на внешнее воздействие, в частности на электрическое поле. Как следует из гипотезы де Бройля и электрон можно считать волной, причем его скорость равна групповой скорости волны де Бройля

(9.31)

Поскольку энергия , соответствующая описываемому данной волновой функцией состоянию, связана с частотой соотношением

Под действием внешнего электрического поля электрон проводимости приобретает среднее ускорение , которое, с учетом формулы (9.32), равно

Но производная d /d определяет среднюю мощность, развиваемую внешней силой , и потому можно написать

Для нахождения продифференцируем формулу (9.32):

и поэтому для среднего ускорения электрона в кристалле получим окончательно

Из полученного равенства (9.36) следует, что среднее ускорение электрона в кристалле пропорционально действующей на него силе внешнего электрического поля. Коэффициентом пропорциональности при этом является величина

1 22 2

Если сравнить полученный результат со вторым законом Ньюто-

играет роль массы электрона при его движении в кристалле. Величина называется эффективной массой электрона. Эффективная масса электрона в кристалле — это масса такого свободного электрона, которую он должен был бы иметь для того, чтобы под действием внешней силы приобрести такое же ускорение, как и электрон в кристалле под действием той же силы.

Введение эффективной массы дает возможность, учитывая сложный характер взаимодействия электрона с кристаллической решеткой при его движении под действием внешнего электрического поля, пользоваться привычными формулами для ускорения, энергии и импульса, определяющими состояние электрона и характеризующими его движение:

494 Электроны в кристаллах [ Гл. 9

Выше, рассматривая возбуждения атомов в кристалле, мы выяснили, что простейшей формой движения атомов является волна смещений с определенными длиной и частотой. Этой волне мы поставили в соответствие квазичастицу — фонон. Теперь мы видим, что электроны в кристалле тоже являются квазичастицами. Поведение электрона удается описать как поведение обычной частицы, но с другой массой. Наиболее характерной особенностью эффективной массы электрона в кристалле является то, что ее величина зависит от направления движения электрона и от его состояния (положения в энергетической зоне). Зависимость эффективной массы от направления движения электрона объясняется анизотропией кристалла: при движении электрона силы взаимодействия его с кристаллической решеткой различны в различных кристаллографических направлениях.

Формирование концепции квазичастиц связано с именем Л.Д. Ландау, который в конце 40-х годов разработал специальный математический аппарат для описания явлений, обусловленных взаимодействием ферми-частиц друг с другом. Этот раздел теоретической физики получил название теории ферми-жидкос- ти. Вначале он был создан для объяснения свойств легкого изотопа гелия (3He) в области температур 0,01–0,1 К, что позволило

свести сложную динамику сильновзаимодействующих частиц к более простой динамике совокупности квазичастиц. Затем теория ферми-жидкости была приспособлена для описания электронов проводимости в металлах.

Поскольку изменение эффективной массы, в соответствие с формулой (9.37), определяется изменением второй производной от кинетической энергии электрона по волновому вектору , для качественного выяснения характера изменения эффективной массы в зависимости от положения электрона в энергетической зоне мы можем использовать приведенный выше закон дисперсии

фик этой функции для первой энергетической зоны кристалла изображен на рис. 9.8 а.

Первая производная (рис. 9.8 б) выражает крутизну функции

и определяет скорость электрона (см. формулу (9.32)),

9.3 ] Динамика электронов в кристаллической решетке 495

вторая производная определяет величину эффективной массы электрона (формула (9.37), рис. 9.8 в)

При малых значениях движение электрона описывается плоской волной, закон дисперсии квадратичный (на рис. 9.8 а он показан тонкой линией). Электрон с малым значением волнового вектора ведет себя как свободный электрон: скорость его под действием внешней силы растет пропорционально волновому вектору, эффективная масса при этом почти неизменна и равна приблизительно массе свободного электрона. С увеличением волнового вектора скорость электрона сначала отстает от роста волнового вектора, а в точке скорость достигает максимума. Эффективная масса с ростом возрастает, а в точке становится бесконечно большой. При дальнейшем увеличении волнового вектора электрона под действием внешнего электрического поля того же направления скорость электрона уменьшается, т. е. он получает отрицательное ускорение — ускорение направлено в сторону, противоположную направлению действующей на него внешней силы. Такое движение электрона с точки зрения классической механики равносильно движению частицы с отрицательной массой.

Но электрон имеет отрицательный электрический заряд, и поэтому его движение в состояниях, соответствующих верхней части энергетической зоны, можно рассматривать как движение положительно заряженной частицы с положительной массой. Такую квазичастицу — частицу с положительной эффективной массой и положительным зарядом, равным по абсолютной величине заряду электрона — называют дыркой и говорят, что кристалл при этом обладает дырочной проводимостью. Особенно удобно введение такой квазичастицы для описания свойств полупроводников, чему посвящен § 9.5.

Отметим, что возбуждение газа фермионов всегда характеризуется появлением свободных состояний — «дырок» — с импульсом Ф и частиц с Ф . Фермиевские возбуждения всегда рождаются парами — частица и дырка.

Следует более подробно разобраться, почему при движении электрона в кристалле масса электрона оказывается переменной. Обратимся для этого к качественному представлению ионного потенциального рельефа как последовательности прямоугольных барьеров. Когда длина волны де Бройля электрона большая (много больше постоянной решетки), то отраженные от различных барьеров волны имеют разные фазы и гасят друг друга, электрон не чувствует наличия периодической структуры, другими

словами, передаваемый решетке импульс очень мал. По мере увеличения энергии электрона (уменьшения его длины волны де Бройля, а значит увеличения величины волнового вектора ), отраженная компонента становится все большей по величине.

Что означает появление отраженной волны? Отраженная волна — это передача импульса от кристаллической решетки к электрону, а значит результирующее приращение импульса под действием внешнего поля становится меньше, чем это бы было в свободном пространстве. Это может быть сказано иначе — эффективная масса электрона увеличивается, электрон становится «тяжелее», его труднее ускорить. Когда от решетки электрону передается больший импульс, чем его приращение за счет внешней силы, эффективная масса становится отрицательной. Сам кристалл при этом испытывает обычную классическую отдачу.

При дальнейшем увеличении , как мы выше видели, скорость электрона не только не увеличивается, а наоборот, уменьшается, хотя направление внешней силы остается неизменным. В точке скорость обращается в нуль: электрон останавливается, несмотря на то, что его импульс достигает максимального значения, равного 2 . С точки зрения величины отраженной волны, ее амплитуда становится равной по величине амплитуде падающей волны и имеет место брэгговское отражение электрона от периодической атомной решетки, его волновой вектор меняется от до и он появляется в точке .

9.4. Электронная тепло- и электропроводность

Теперь мы можем перейти к рассмотрению вопроса о кинетике электронов проводимости, что прямо связано с рассеянием в электрон-фононной системе. Зная характеристики квазичастиц, можно получить термодинамическое описание системы многих частиц с сильным взаимодействием при 0 K, исходя из картины идеального газа квазичастиц.

Квазиимпульс электрона не изменяется при движении в поле идеальной решетки, его изменение может произойти только под влиянием непериодической части потенциального поля. Это означает, что рассеяние электронов происходит на любых нарушениях идеальной структуры решетки, возникающих из-за тепловых колебаний (газа фононов), дефектов решетки (дислокации, вакансии, примесные атомы), отклонения от периодичности самосогласованного потенциала электронов.

Рассматривая электроны как газ свободных квазичастиц, мы легко можем, аналогично тому, как это делалось в случае решеточной (фононной) теплопроводности, найти качественно температурную зависимость электронной теплопроводности. Из газо-

9.4 ] Электронная тепло- и электропроводность 497

кинетической теории следует, что коэффициент теплопроводности равен

13 , (9.40)

где — теплоемкость носителей, — их скорость, 1 эф — их длина свободного пробега ( эф, — эффективное сечение рассеяния и концентрация рассеивающих центров соответственно). У электронов, участвующих в кинетических явлениях, скорость мало отличается от фермиевской (их энергия увеличивается примерно на Б ), теплоемкость линейно зависит от температуры, и нужно лишь определить температурную зависимость длины свободного пробега электронов.

Рассмотрим вначале область высоких температур . Так как в этой области температур фононы преимущественно дебаевские, то число фононов пропорционально температуреБ Д . В то же время сечение рассеяния электронов на фононе не зависит от температуры по тем же причинам («размер» фононов одинаков). Поэтому длина свободного пробега

эф

Так как электронная теплоемксть линейно зависит от температуры (см. (9.21)), то согласно (9.40) коэффициент электронной теплопроводности является постоянной величиной.

По мере уменьшения температуры число фононов уменьшается как 3 (энергия фононного газа пропорциональна 4, а число фононов на одной моде есть Б ). Для оценки можно считать, что сечение рассеяния слабо зависит от температуры, и мы

большей части теплового потока в металлах — электроны или фононы? Экспериментально известно, что нормальные чистые

металлы при комнатных температурах имеют теплопроводность на один-два порядка величины большую, чем твердые диэлектрики. Действительно, простая оценка показывает, что теплоперенос в металлах преимущественно осуществляется электронами. Отношение электронной теплопроводности к решеточной равно

В неупорядоченных сплавах длины свободного пробега как фо-

нонов, так и электронов определяются главным образом структурными неоднородностями кристаллической решетки и в них электронная теплопроводность может быть по порядку величины равна решеточной.

Теперь обратимся к вопросу об электропроводности. Вначале опишем ее на феноменологическом языке. Под действием приложенного электрического поля напряженностью электрон с эффективной массой на длине свободного пробега (за время между соударениями ) приобретает средний импульс и среднюю дрейфовую скорость Д такие, что

Если ввести подвижность электрона в поле, т. е. ту среднюю скорость направленного движения, которую электрон приобретает в поле единичной напряженности, то

Если проводимость металла равна , то закон Ома записывается в виде и для металла с концентрацией электронов

Итак, для расчета проводимости металла необходимо знать длину свободного пробега электронов. В феноменологической теории длина свободного пробега задается как параметр; оценим ее на основе развитых выше представлений о поведении электронов в кристаллах.

Из эксперимента известно, что в области не слишком низких температур сопротивление металла с примесями ведет себя в соответствии с так называемым правилом Матиссена, согласно которому сопротивление может быть представлено в виде суммы двух частей: зависящего от температуры сопротивления идеального беспримесного металла ид , которое при

описывается законом Блоха–Грюнайзена ид 5 и стремится к нулю при 0, и не зависящего от температуры остаточного

9.4 ] Электронная тепло- и электропроводность 499

сопротивления 0, которое полностью определяется концентрацией примесей:

Начнем, как и в случае теплопроводности, с области высоких температур ( . В этой области число фононов растет линейно с температурой в силу того, что практически все фононы одной частоты (дебаевской), сечение электрон-фононного рассеяния одинаково (не зависит от температуры) и поэтому сопротивление линейно растет с температурой в полном соответствии с хорошо известным законом

При обычных температурах (комнатных и более высоких) отношение , как следует из экспериментов, оказывается постоянной величиной, не зависящей ни от температуры, ни от сорта металла, и эта закономерность получила название закона Видемана–Франца (по имени немецких физиков Г. Видемана (1826–1899) и Р. Франца). Действительно, воспользовавшись полученными ранее выражениями (9.21), (9.40) и (9.45) для теплопроводности и электропроводности металлов, мы получаем:

в этой формуле равен 2 3. Закон Видемана–Франца — прекрасное доказательство правильности наших воззрений на «устройство» металла.

Однако исследования электропроводности и теплопроводности при низких температурах показали, что закон Видемана– Франца не универсален. Все дело в том, что в области низких температур далеко не каждое электрон-фононное столкновение приводит к «выбиванию» электрона из процесса переноса заряда. Причина столь неэффективного электрон-фононного взаимодействия состоит в следующем. При столкновении с фононом электрон не может изменить свой импульс э Ф Б

на величину, большую импульса фонона Ф Ф Ф

Б . В приведенных оценках мы воспользовались тем, что в области низких температур ( ) возбуждаются преимущественно длинноволновые фононы с энергией Б и законом дисперсии Ф Ф , а также оценкой (9.6) для фермиевского импульса и (8.29) для температуры Дебая. Хотя при низких температурах импульс фонона мал по сравнению с фермиевским импульсом электрона ( Ф э ), этой передачи импульса достаточно, чтобы «горячий» электрон сделать уже при одном

столкновении с фононом «холодным», и поэтому длина свободного пробега определяется лишь числом фононов. В электропроводности под длиной свободного пробега понимается длина, на которой электрон полностью теряет свою скорость направленного движения, обусловленную приложенным электрическим полем, т. е. его импульс (фермиевский) должен измениться на величину порядка самого импульса. Поэтому один акт электрон-фононного рассеяния оказывается малоэффективным и необходимо большое

число таких столкновений, чтобы остановить электрон, вернее повернуть его импульс на угол порядка 2.

2 Количественное рассмотрение этого процесса показывает, что сопротивление в области низких температур растет, как указывалось выше, пропорционально пятой степени температуры. Когда длина свободного пробега электрона начинает ограничиваться примесями и дефектами, она становится температурно независимой и сопро-

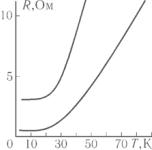
тивление, которое называется остаточным, становится практически постоянным сопротивлением. В неупорядоченных сплавах даже при комнатной температуре сопротивление может обусловливаться главным образом неоднородностями. В качестве иллюстрации рассмотренных выше закономерностей температурного хода сопротивления металлов на рис. 9.10 приведены результаты измерения температурной зависимости сопротивления медной (1) и платиновой (2) проволок диаметром 0,04 мм и длиной 2000 см.

9.5. Электроны в полупроводниках

Полупроводниками принято называть вещества с полностью заполненной валентной зоной, отсутствием электронов в зоне проводимости при 0 К и величиной щели (запрещенной зоны) меньше или порядка 3 эВ. При абсолютном нуле температур полупроводники являются изоляторами, а при комнатной температуре проводят, хотя и слабо (число электронов в зоне проводимости составляет при этом всего около 10 числа атомов).

Переход электрона из валентной зоны в зону проводимости сопровождается появлением «свободного места» в электронном спектре. Электрон, оказавшийся на одном из разрешенных уровней зоны проводимости, может свободно перемещаться под действием электрического поля, т. е. создавать ток. В то же время, на вакантный уровень в валентной зоне может переместится